第十一章 图论 Part7

目录

• 最小生成树算法
  • prim算法
    • 适用范围：无向图
    • 思路
  • kruskal算法
    • 适用范围: 无向图
    • 思路

最小生成树算法

prim算法

适用范围：无向图

思路

以将所有点归入最小生成树为目标，每次并入一个，最终生成最小生成树。
每次并入的步骤：

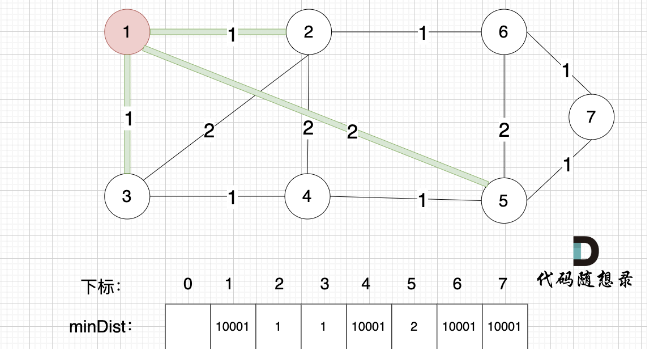
1. 确定选哪个节点并入 （不在最小生成树里的，距离最小生成树（已并入的点）最小的节点） 遍历每个点，得到最小距离的那个点及最小距离。 (顶点编号）
2. 将第一步选到的点加入到最小生成树中，用一个bool列表记录已经加入的点。
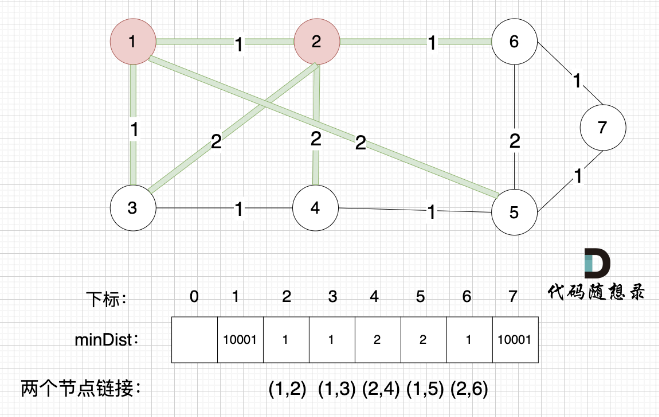
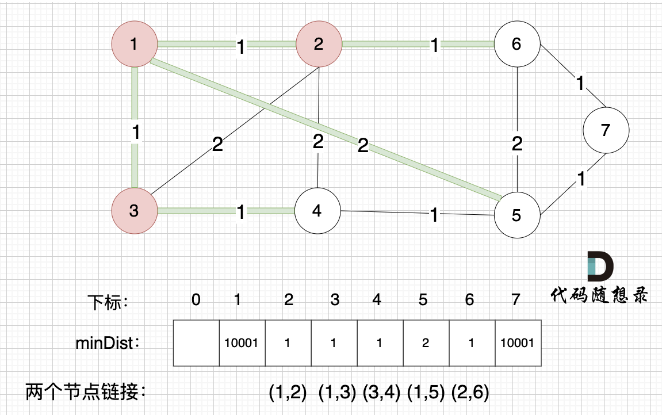
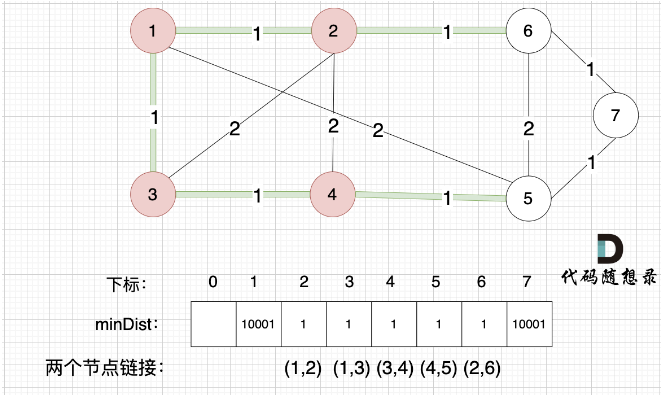
3. 更新非生成树节点到生成树的距离。 （与cur相连的某节点的权值，比该节点距离最小生成树小 =》 因为cur加入最小生成树后，其他节点需要更新距离这个最新形成的部分最小生成树距离） =》 观察4这个节点随着各个节点的加入，距离最小生成树的最小值的变化；以及最终作为被选取的点加入到最小生成树的过程。

如果想记录这个最小生成树的边，则使用parent数组（元素值表示使当前节点更新的前一个节点），在第三步更新时记录即可，如果后续节点的加入还会使该点更新，则parent数组实际也会更新。

v,e = map(int,input().split()) # 顶点数，边数

graph = [[float('inf')]* (v+1) for _ in range(v+1)] #邻接矩阵

for _ in range(e):
    x,y,k = map(int,input().split())
    #无向图关于对角线对称，x到y的距离与y到x的距离相等
    graph[x][y] = k
    graph[y][x] = k

inTreePoints = [False]* (v+1) #是否加入到最小生成树中
minValVec = [float('inf')]* (v+1) #所有点的最小距离列表,初始化每个距离为inf

for i in range(1,v):  # 选完v-1个点，最后一个也确认了，它们一起构成最小生成树
    #1. 确认新加入的点的编号
    cur = 1
    minDist = float('inf') #最大的权值 
    for j in range(1,v+1): #遍历所有还未加入最小生成树的点，确认要新加入的点的编号
         
        if not inTreePoints[j] and minValVec[j] < minDist:
            minDist = minValVec[j] #更新最小距离,以便在后续迭代中继续比较
            cur = j #更新新加入的点的编号，当循环退出时，确定新加入的点的编号
    
    #2.记录新加入的点
    inTreePoints[cur] = True
    
    #3.因为最小生成树有了新加入的点，更新每个未确定的点到部分最小生成树的最小距离
    for j in range(1,v+1):
        if (not inTreePoints[j] and graph[cur][j] < minValVec[j]):#某点到最小生成树的距离可能由于最小生成树新加入了点而改变
            minValVec[j] = graph[cur][j]
    
    

res = 0
for i in range(2,v+1):
    res+=minValVec[i]

print(res)

kruskal算法

适用范围: 无向图

思路

以边为中心考虑，不断去添加最小的边合成一个集合（注意要添加不在一个集合的边，否则就是冗余边，会形成环），刚开始组成的图有可能是不连通的，但随着边的添加，最后一定会形成连通图，并且是最小连通子图即最小生成树，这种将点放入同一集合，判断点是否在同一集合中的逻辑，使用并查集来实现。下面简单给出算法（未给输入）。如果需要记录最小生成树的边，对于kruskal算法非常简单，join时添加当前边即可。

class UnionFind:
    def __init__(self,n):
        self.father = [0] * (n+1)
        for i in range(1,n+1):
            self.father[i] = i
        
    # （查） 
    def find(self,u): 
        if u == self.father[u]:
            return u
        else:
            self.father[u] = self.find(self.father[u])  # 路径压缩(一直像上层返回最底层的值，并且一直赋值)
            return self.father[u]
 
    # 判断 u 和 v 是否找到同一个根
    def is_same(self,u, v): 
        u = self.find(u)
        v = self.find(v)
        return u == v
 
    # 将 v->u 这条边加入并查集 （并）
    def join(self,u, v):
        u = self.find(u)  # 寻找 u 的根
        v = self.find(v)  # 寻找 v 的根
        if u == v:
            return  # 如果发现根相同，说明在一个集合，不用两个节点相连，直接返回
        self.father[v] = u #否则其中一根归于另一根

#kruskal算法
#1.按照边的权值由小到大排序
edges.sort(key=lambda x: x[2])
unionFind = UnionFind(v+1)

res = 0
for edge in edges:
  if not unionFind.is_same(edge[0],edge[1]):
    res += edge[2]
    join(edge[0],edge[1])