面向对象设计与构造-第一单元总结

面向对象设计与构造-第一单元总结

第一次作业

1 题目描述

读入一个包含加、减、乘、乘方以及括号（其中括号的深度至多为 1 层）的单变量表达式，输出恒等变形展开所有括号后的表达式。

2 整体架构

本次作业的UML图如下所示：

3 类的设计

3.1 ExpMap类

ExpMap类是本次作业中的核心，是对任意多项式的统一表示，并实现了多项式的加法与乘法，以及生成多项式字符串的toString()方法。所有多项式成分的类均包含一个ExpMap的成员变量。

ExpMap类的成员变量只包括一个名为map的HashMap，其中的key代表的是变量x的指数，value则是x的系数，各组<key,value>之间是相加的关系，可表示为如下公式(为表示方便，公式中对HashMap中元素的表示并不符合Java语法)：

$$\sum _{i=0}^n map.value_i * x ^ {map.key_i}$$

ExpMap中实现了用于加法和乘法运算的add()方法和mul()方法，在程序中需要进行任何计算时，都可以通过直接调用这两个函数来实现。这一设计的灵感来自于BigInteger中运算方法的设计。

3.2 Expression类

Expression类代表的是”表达式”。通过形式化表述不难看出，表达式是由‘+’或‘-’连接的项，因此，在Expression类中以ArrayList<item>来记录该表达式的各个项。

3.3 Item类

Item类代表的是”项”。与Expression类类似，Item类中以ArrayList<Factor>来记录该项中各以‘*’相连的因子。

3.4 Factor类

Factor类是所有因子的父类。大部分同学在实现Factor时采用的是接口，而我在设计时由于需要Factor拥有一个ExpMap类的成员变量，因此没有使用接口。Factor的子类即各种因子，子类的构造方法负责Factor中成员变量ExpMap的构造。

3.5 ExpFactor类

ExpFactor类代表的是“表达式因子”，是Factor的子类。该类中Expression类型的成员变量即因子的表达式部分，index则为表达式的指数。

3.6 ConstFactor类与VariableFactor类

ConstFactor类与VariableFactor类分别代表“常量因子”与“变量因子”，是Factor的子类。

3.7 FactorFactory类

在Item中，我们将其字符串分隔为多个相乘的因子，此时我们并不知道因子的具体类型，因此在因子的构建上采用了工厂模式，FactorFactory即用于构建各种因子的“工厂”。

4 复杂度分析

4.1 类复杂度

Class	OCavg	OCmax	WMC
ConstFactor	1	1	1
ExpFactor	2.5	3	5
ExpMap	3.71	15	26
Expression	3.6	9	18
Factor	1	1	3
FactorFactory	2	3	4
Item	5	10	15
Main	1	1	1
VariableFactor	2	2	2

4.2 方法复杂度

Method	CogC	ev(G)	iv(G)	v(G)
ConstFactor.ConstFactor(String)	0	1	1	1
ExpFactor.ExpFactor(String)	2	1	2	2
ExpFactor.setExp()	2	2	3	3
ExpMap.ExpMap()	0	1	1	1
ExpMap.add(ExpMap)	3	1	3	3
ExpMap.copy()	0	1	1	1
ExpMap.getMap()	0	1	1	1
ExpMap.mul(ExpMap)	6	1	4	4
ExpMap.toString()	40	3	15	19
ExpMap.update(BigInteger, BigInteger)	0	1	1	1
Expression.Expression(String)	13	1	7	10
Expression.getExpMap()	0	1	1	1
Expression.isAddOrMinus(char)	1	1	1	2
Expression.setExpMap()	2	2	2	3
Expression.strProcedure(String)	7	1	4	5
Factor.Factor()	0	1	1	1
Factor.getExpMap()	0	1	1	1
Factor.setExpMap(ExpMap)	0	1	1	1
FactorFactory.getFactor(String)	4	3	3	4
FactorFactory.isAddOrMinus(char)	1	1	1	2
Item.Item(String)	12	1	6	10
Item.getExpMap()	0	1	1	1
Item.setExp()	3	2	3	4
Main.main(String[])	0	1	1	1
VariableFactor.VariableFactor(String)	2	1	2	2

总体来看，本次作业的复杂度是较低的。只有ExpMap类中用于生成多项式字符串的toString()方法由于需要对多种情况进行判断，导致复杂度较高。

5 优化

第一次作业中，由于多项式较为简单，因此优化的空间并不大，只要做好同类项合并就基本达到了最优的长度，在我的设计中，ExpMap就可以较为方便地进行同类项合并。此外还有一些比较小的可以优化的点，例如将正项作为多项式的第一个项（如果有正项的话），将x**2改为x*x等。

6 测试

本次作业中，我在公测和互测中均未出现Bug，也没有在互测中找到其他同学的Bug。

7 总结

第一次作业的难度不是特别大，但是对于整个第一单元来说是至关重要的。如果本次作业中能够充分应用面向对象设计的思想，构建出良好的代码结构，不仅可以避免迭代开发中的大规模重构，减轻之后作业的工作量，还可以对正确率提供较好的保障。

第二次作业

1 题目描述

读入一系列自定义函数的定义以及一个包含简单幂函数、简单三角函数、简单自定义函数调用以及求和函数的表达式，输出恒等变形展开所有括号后的表达式。

2 整体架构

本次作业的UML图如下所示：

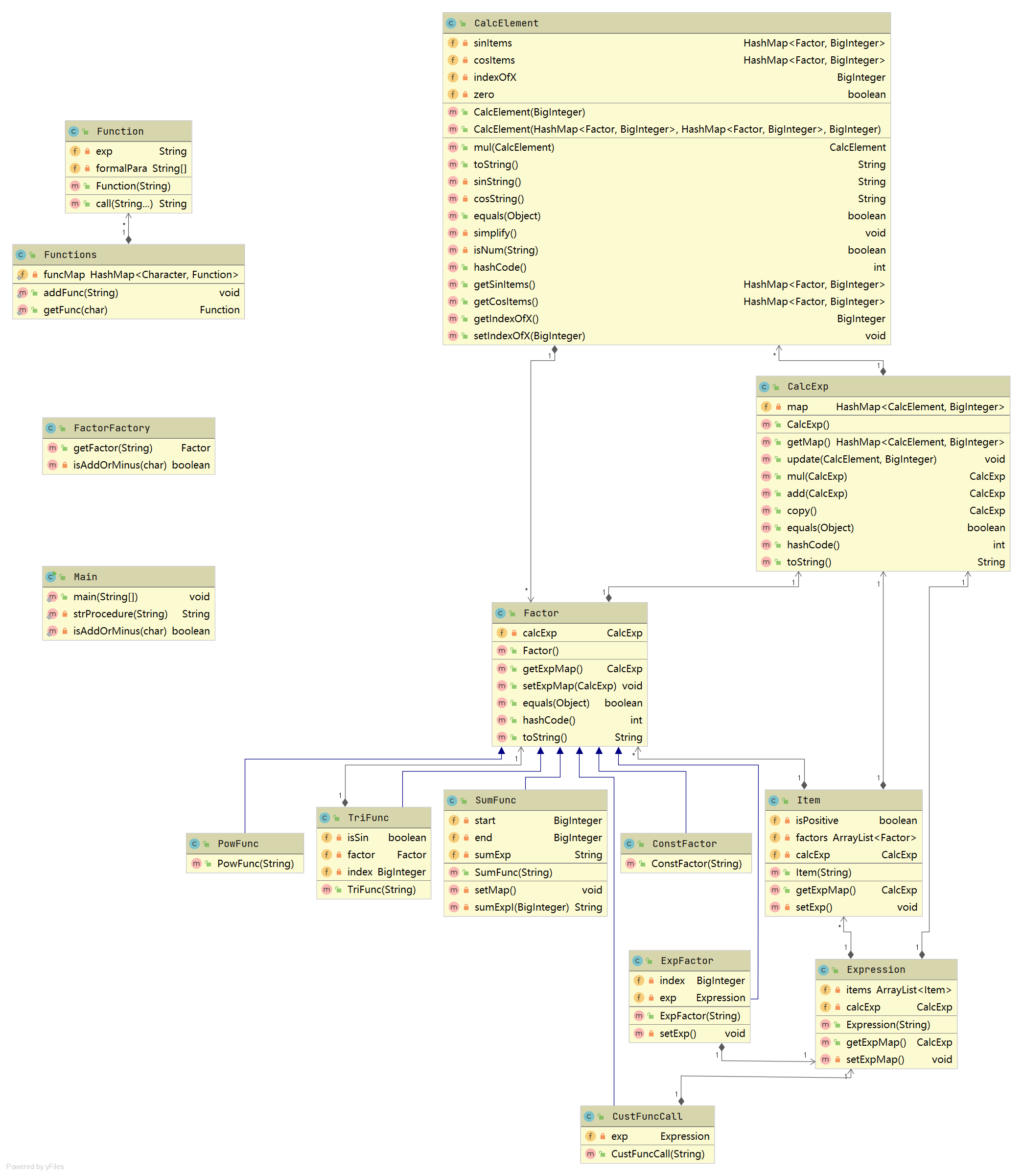
3 类的设计

3.1 CalcElement类

本次作业的多项式复杂度大大增加，无法再像上一次作业中仅通过一个HashMap来表示整个多项式，因此设计了CalcElement类。

数据结构上，sinItems和cosItems的类型为HashMap<Factor, BigInteger>，分别表示sin和cos两种三角函数，Factor类型的key为三角函数括号内的项，BigInteger类型的value代表指数。x的指数则用BigInteger类型的indexOfX表示。其所代表的多项式可以表示为：

$$\Pi_{i=1}^m sin(sinItems.key_i)^{sinItems.value_i} * \Pi_{j=1}^n cos(cosItems.key_j)^{cosItems.value_j} * x ^{indexOfX}$$

此类中实现了用于乘法计算的mul()函数。

3.2 CalcMap类

CalcMap类延续了第一次作业中ExpMap类的设计思想，将map的类型更改为了HashMap<CalcElement, BigInteger>，value代表的是对应CalcElenment类型的key的系数。同时也对用于计算的add()和mul()函数进行了相应的修改。CalcMap所表示的多项式如下公式所示：

$$\sum _{i=1}^n map.key_i ^ {map.key_i}$$

3.3 TriFunc类

TriFunc类代表的是“三角函数”，是Factor的子类。isSin标识该类是sin还是cos，factor是三角函数括号内的项，index是三角函数的指数，解析出以上成员变量后，对父类中的calcExp进行赋值。

3.4 SumFunc类

SumFunc类代表的是“求和函数”，是Factor的子类。构造SumFunc时，先从输入字符串中解析出i的范围[start, end]以及求和表达式sumExp，然后对于每一个i的值，都构造一个相应的Expression类的对象，并将这些对象相加，从而得到对应的父类中的CalcExp。

3.5 Function类

Function类用于存放函数定义，其成员变量exp代表函数表达式，formalPara记录所有的形参。该类的call()方法的参数是调用该函数时的实参，返回的是将该自定义函数的所有形参替换为对应实参后的字符串。

3.6 Functions类

Functions类用于存放所有的自定义函数，其成员变量funcMap即为自定义函数的容器。funcMap的key是函数名，value是对应的Function类的对象。由于自定义函数的输入先于表达式，因此funcMap设为了static类型，以便于存储函数定义。

3.7 CustFuncCall类

CustFuncCall类代表“自定义函数调用“，是Factor的子类。构造方法中，先通过Functions类获取对应的函数定义f，然后向f的call()传入参数的表达式以获得对应的多项式字符串，最后用该字符串创建表达式exp。并对父类的calcExp赋值。

3.8 FactorFactory类

FactorFactory类在第一次作业的基础上，增加了对PowFunc、TriFunc、CustFuncCall、SumFunc等类的构建。

3.9 其他

Expression类、Item类、Factor类、ExpFactor类、ConstFactor类、PowFunc类等相较于第一次作业没有改动或仅重载了hashcode()和equals()方法。

4 复杂度分析

4.1 类复杂度

Class	OCavg	OCmax	WMC
CalcElement	3.71	11	52
CalcExp	3.33	15	30
ConstFactor	1	1	1
CustFuncCall	1	1	1
ExpFactor	2.5	3	5
Expression	4.33	9	13
Factor	1.33	3	8
FactorFactory	3.5	6	7
Function	1.5	2	3
Functions	1.5	2	3
Item	5	10	15
Main	2.33	4	7
PowFunc	2	2	2
SumFunc	1.67	2	5
TriFunc	3	3	3

4.2 方法复杂度

Method	CogC	ev(G)	iv(G)	v(G)
CalcElement.CalcElement(BigInteger)	0	1	1	1
CalcElement.CalcElement(HashMap<Factor, BigInteger>, HashMap<Factor, BigInteger>, BigInteger)	2	1	3	3
CalcElement.cosString()	12	4	5	6
CalcElement.equals(Object)	4	3	4	6
CalcElement.getCosItems()	0	1	1	1
CalcElement.getIndexOfX()	0	1	1	1
CalcElement.getSinItems()	0	1	1	1
CalcElement.hashCode()	0	1	1	1
CalcElement.isNum(String)	5	4	4	6
CalcElement.mul(CalcElement)	6	1	5	5
CalcElement.setIndexOfX(BigInteger)	0	1	1	1
CalcElement.simplify()	24	9	13	13
CalcElement.sinString()	12	4	5	6
CalcElement.toString()	12	2	3	8
CalcExp.CalcExp()	0	1	1	1
CalcExp.add(CalcExp)	3	1	3	3
CalcExp.copy()	0	1	1	1
CalcExp.equals(Object)	3	3	2	4
CalcExp.getMap()	0	1	1	1
CalcExp.hashCode()	0	1	1	1
CalcExp.mul(CalcExp)	6	1	4	4
CalcExp.toString()	43	3	20	20
CalcExp.update(CalcElement, BigInteger)	0	1	1	1
ConstFactor.ConstFactor(String)	0	1	1	1
CustFuncCall.CustFuncCall(String)	0	1	1	1
ExpFactor.ExpFactor(String)	2	1	2	2
ExpFactor.setExp()	2	2	3	3
Expression.Expression(String)	13	1	7	10
Expression.getExpMap()	0	1	1	1
Expression.setExpMap()	2	2	2	3
Factor.Factor()	0	1	1	1
Factor.equals(Object)	3	3	2	4
Factor.getExpMap()	0	1	1	1
Factor.hashCode()	0	1	1	1
Factor.setExpMap(CalcExp)	0	1	1	1
Factor.toString()	0	1	1	1
FactorFactory.getFactor(String)	10	6	7	13
FactorFactory.isAddOrMinus(char)	1	1	1	2
Function.Function(String)	0	1	1	1
Function.call(String...)	1	1	2	2
Functions.addFunc(String)	1	1	1	2
Functions.getFunc(char)	0	1	1	1
Item.Item(String)	12	1	6	10
Item.getExpMap()	0	1	1	1
Item.setExp()	3	2	3	4
Main.isAddOrMinus(char)	1	1	1	2
Main.main(String[])	1	1	2	2
Main.strProcedure(String)	7	1	4	5
PowFunc.PowFunc(String)	2	1	2	2
SumFunc.SumFunc(String)	0	1	1	1
SumFunc.setMap()	1	1	2	2
SumFunc.sumExpI(BigInteger)	1	2	1	2
TriFunc.TriFunc(String)	5	1	3	4

本次作业中，除了ExpMap类中的toString()方法复杂度依然较高外，用于表达式化简的CalcElement的simplify()方法复杂度也较高。

5 优化

在第一次作业的基础上，我增加了对三角函数特殊值的优化，即当三角函数内的项为90的倍数或0时，直接将其值(0、1或-1)作为表达式的一部分。值得一提的是，虽然本次作业中多项式的表示复杂了很多，但得益于hashCode()和equals()的重载，依然较为轻松地实现了同类相的合并。

6 测试

6.1 被发现的Bug

本次作业中，我在公测和互测中均未被发现Bug。

6.2 发现别人的Bug

在第二次作业的互测中，发现了其他同学程序中的一些Bug，下面选取较有代表性的进行总结：

• 指数大小问题

  第一次作业中对指数大小的限制并不适用，一些同学未对这一部分进行修改。hack时所用样例如下：

  0
  (1)**10
  

• 三角函数优化导致错误

  一些同学在对三角函数的特殊值进行优化时出现了Bug，hack用例如下：

  0
  sin(76)
  

7 总结

本次作业相较于第一次来说，难度提升是比较大的，个人认为难点主要在于多项式的合理表示，以及两种函数的处理上。我在本次作业中的工作主要包括多项式的表示方法的调整，以及对于新增语法成分的类的构建。得益于第一次作业中合格的架构设计，我在本次作业中并未经历大规模的重构，这也让我深刻体会到了合理架构的重要性。

第三次作业

1 题目描述

读入一系列自定义函数的定义以及一个包含幂函数、三角函数、自定义函数调用以及求和函数的表达式，输出恒等变形展开所有括号后的表达式。

2 整体架构

本次作业的UML图与第二次作业相比，仅新增了StringDec类，该类与其他类之间没有结构上的关联，因此不再另外展示。

3 类的设计

3.1 CustFuncCall类

CustFuncCall类是相较于第二次作业唯一有所改动的类。区别在于，第二次作业中由于数据限制，函数调用中的实参中不会出现逗号，因此可以直接使用split()方法来获得实参。而本次作业中由于函数也可以作为实参，因此需要对字符串进行一定的解析。

3.2 StringDec类

StringDecl类是本次作业中唯一新加的类，包含一个static方法strProcedure()，用于对字符串进行初始的处理，如去空格等操作。本质上只是将第二次作业中的相关代码单独整理了出来，增强代码的可读性。

3.3 其他

相较于第二次作业，其他的类均没有本质上的改动。

4 复杂度分析

4.1 类复杂度

Class	OCavg	OCmax	WMC
CalcElement	3.29	8	46
CalcExp	3.33	15	30
ConstFactor	1	1	1
CustFuncCall	4.67	9	14
ExpFactor	2.5	4	10
Expression	4.33	9	13
Factor	1.33	3	8
FactorFactory	3.5	6	7
Function	3	5	6
Functions	1.5	2	3
Item	5	10	15
Main	2	2	2
PowFunc	2	2	2
StringDeal	2.5	4	5
SumFunc	2	4	10
TriFunc	4.5	9	18

4.2 方法复杂度

Method	CogC	ev(G)	iv(G)	v(G)
CalcElement.CalcElement(BigInteger)	0	1	1	1
CalcElement.CalcElement(HashMap<Factor, BigInteger>, HashMap<Factor, BigInteger>, BigInteger)	2	1	3	3
CalcElement.cosString()	18	4	7	8
CalcElement.equals(Object)	4	3	5	7
CalcElement.getCosItems()	0	1	1	1
CalcElement.getIndexOfX()	0	1	1	1
CalcElement.getSinItems()	0	1	1	1
CalcElement.hashCode()	0	1	1	1
CalcElement.isExp(String)	1	1	2	2
CalcElement.mul(CalcElement)	12	2	7	9
CalcElement.setIndexOfX(BigInteger)	0	1	1	1
CalcElement.setZero(boolean)	0	1	1	1
CalcElement.sinString()	18	4	7	8
CalcElement.toString()	12	2	3	8
CalcExp.CalcExp()	0	1	1	1
CalcExp.add(CalcExp)	3	1	3	3
CalcExp.copy()	0	1	1	1
CalcExp.equals(Object)	3	3	2	4
CalcExp.getMap()	0	1	1	1
CalcExp.hashCode()	0	1	1	1
CalcExp.mul(CalcExp)	6	1	4	4
CalcExp.toString()	43	3	20	20
CalcExp.update(CalcElement, BigInteger)	0	1	1	1
ConstFactor.ConstFactor(String)	0	1	1	1
CustFuncCall.CustFuncCall(String)	9	1	5	8
CustFuncCall.equals(Object)	4	4	2	5
CustFuncCall.hashCode()	0	1	1	1
ExpFactor.ExpFactor(String)	2	1	2	2
ExpFactor.equals(Object)	5	4	3	6
ExpFactor.hashCode()	0	1	1	1
ExpFactor.setExp()	2	2	3	3
Expression.Expression(String)	13	1	7	10
Expression.getExpMap()	0	1	1	1
Expression.setExpMap()	2	2	2	3
Factor.Factor()	0	1	1	1
Factor.equals(Object)	3	3	2	4
Factor.getExpMap()	0	1	1	1
Factor.hashCode()	0	1	1	1
Factor.setExpMap(CalcExp)	0	1	1	1
Factor.toString()	0	1	1	1
FactorFactory.getFactor(String)	10	6	7	13
FactorFactory.isAddOrMinus(char)	1	1	1	2
Function.Function(String)	0	1	1	1
Function.call(String...)	6	1	5	5
Functions.addFunc(String)	1	1	1	2
Functions.getFunc(char)	0	1	1	1
Item.Item(String)	12	1	6	10
Item.getExpMap()	0	1	1	1
Item.setExp()	3	2	3	4
Main.main(String[])	1	1	2	2
PowFunc.PowFunc(String)	2	1	2	2
StringDeal.isAddOrMinus(char)	1	1	1	2
StringDeal.strProcedure(String)	7	1	4	5
SumFunc.SumFunc(String)	0	1	1	1
SumFunc.equals(Object)	5	4	4	7
SumFunc.hashCode()	0	1	1	1
SumFunc.setMap()	1	1	2	2
SumFunc.sumExpI(BigInteger)	1	2	1	2
TriFunc.TriFunc(String)	21	1	11	12
TriFunc.equals(Object)	5	4	4	7
TriFunc.hashCode()	0	1	1	1
TriFunc.isNum(String)	5	4	4	6

本次作业中，ExpMap类中的toString()方法复杂度依然较高。此外，本次作业中我把三角函数特殊值的化简由CalcElement中的simplify()方法整理到了TriFunc()的构造方法中，从而使得TriFunc()复杂度较高。

5 优化

考虑到本次作业中三角函数括号内的因子可能是表达式因子，在第二次作业的基础上增加了相应的优化：对于三角函数括号内符合”常数因子“、”幂函数“和”三角函数“的因子，在生成输出字符串时不在其两边增加括号。

6 测试

6.1 被发现的Bug

本次作业中，我在互测阶段被发现了Bug，具体为：

• 三角函数括号内因子优化导致的问题

  上文提到我所做的针对三角函数括号内因子的优化，很不幸地引入了Bug。我在判断因子是否为三角函数时，使用的正则表达式为：

  String triFactor = "((sin)|(cos))\\(.*\\)(\\*\\*(\\+)?\\d+)?";
  

  不难发现对于如下的样例，使用该正则表达式将会导致将表达式误判为三角函数：

  0
  sin(sin(x)*cos(x))
  

  该Bug是我在互测阶段是就发现的，同时也hack到了另外两位同学。

6.2 发现别人的Bug

除了上面提到的Bug外，我在互测阶段发现的Bug还有：

• 数据溢出问题

  不合适的数据类型在面对较大的数据时会导致溢出，hack用例如下：

  0
  sum(i,111111111111,111111111121,i)
  

• 函数调用的参数顺序问题

  一些同学在函数调用上，使用的方法是用实参依次替换形参。那么当形参中y出现在x之前，而y所代表的实参中又包含x时，将会导致替换形参x时将之前实参中的x也替换掉。hack用例如下：

  1
  f(y, x) = x * y
  f(x, y)
  

  可惜的是互测中不允许出现自定义函数。

7 总结

在做第二次作业时我就在想，题目都出到这种程度了，第三次作业还能怎么出？果然，第三次作业仅仅是删去了一些数据限制。而我在完成前两次作业时，根本没有考虑这些数据限制，而是直接从形式化表述入手构建的整个程序。现在看来，这样的思路是十分正确的，它让我在半小时内完成了第二次作业到第三次的迭代。再次感叹合理的架构设计的重要性。

架构设计体验

1 三次作业的迭代

三次作业迭代的细节，在每次作业的相应位置都给出了具体的阐释，这里不再赘述。在这里我想总结一下整个过程中让我受益较大的设计思想：

• 面向对象

  把”面向对象“写在这里似乎是在废话，但不得不说，第一单元的作业不断的设计与迭代，的确让我越来越深刻地体会到面向对象的优势与重要性，这或许是看再多文字描述都无法体会到的。

• 递归下降

  递归下降可以说是第一单元最最重要的思想了，在理解了递归下降并充分应用后，不仅可以降低我们程序的复杂度，还可以提高可扩展性和正确性。

• 适度忽略数据限制

  题目中的一些限制，的确可以一定程度地简化程序的设计，但代价是会增加迭代开发时重构的风险，同时也很可能因为边界情况考虑不周引入一些Bug。”忽视数据限制“这一思想的本质在于为将来可能出现的更复杂的情况留下处理的空间。正是得益于这样的思想，我才能够平滑地完成第一次到第二次的迭代，并在极短的时间内完成第三次作业。

2 心得体会

• 注重设计

  很多时候我们都会抱着”车到山前必有路“的想法迫不及待地开始编写代码，即使我们心中还没有建立起较为完整的设计。本单元的作业则让我深刻意识到了提前设计的重要性，也体会到了好的设计带来的裨益。

• 不做ddl选手

  OO课的时间安排紧凑而充实，同时课程难度也较大，因此我们应该尽早开始着手完成作业，避免临近截止时间的手忙脚乱。

• 对本单元作业的评价

  整体上我对本单元的作业是持肯定态度的，它的确给了我很大的收获。但明显能够看得出来的是，本单元的作业中有非常多的数据限制，有一种”束手束脚“的感觉，在第二次作业中尤为明显。这些限制不仅让题目描述有些冗长，也无形地增加了理解上的负担。非常理解课题组处于整体难度的把握而进行的数据限制，但我认为适当降低题目复杂度，而减少数据限制，可能是更加合理的做法。