字符串相似度的计算(百度笔试题回忆)
题目
这道题应该说很出名了,原题见字符串相似度的计算,但是考试的时候真的想不出怎么实现。看了解答方法后,我现在就把实现方法说一下:
如果仅仅只计算字符串的距离,则只需以下3个步骤
如果需要把字符串转变的过程记录下来,则需要6个步骤
粗略解法
下面我就先实现只计算字符串距离的代码,使用了模板。这种方法虽然可以计算出结果来,但是重复计算非常多,后面会有个对比的。
//字符串相似度的计算,模板实现,可用于其他容器 #include <string> #include <iostream> using namespace std; template<typename Iterator> int caculateDistance(Iterator pAbegin, Iterator pAend, Iterator pBbegin, Iterator pBend) { if (pAbegin>pAend) { if (pBbegin>pBend) return 0; else return pBend-pBbegin+1; } if (pBbegin>pBend) { if (pAbegin>pAend) return 0; else return pAend-pAbegin+1; } if (*pAbegin == *pBbegin) { return caculateDistance(pAbegin+1,pAend,pBbegin+1,pBend); } else { int t1 = caculateDistance(pAbegin+1,pAend,pBbegin+2,pBend); int t2 = caculateDistance(pAbegin+2,pAend,pBbegin+1,pBend); int t3 = caculateDistance(pAbegin+2,pAend,pBbegin+2,pBend); int minValue = t1>t2?t2:t1; minValue = minValue>t3?t3:minValue; return minValue+1; } } int main() { string A = "abcdefghijklmn"; string B = "cdefghijklmn"; cout << caculateDistance(A.begin(),A.end(),B.begin(),B.end()) << endl; return 0; }
解法改进
考虑到有些数据被重复计算的情况(字符串相似度的计算中实现了存在数据重复计算的情况的代码),就把子问题的结果保存起来以备后查。
历史记录结构体
结构体定义如下:
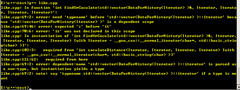
//存储历史记录的结构体 template<typename Iterator> struct DataForHistory { DataForHistory(Iterator iAbegin, Iterator iAend, Iterator iBbegin, Iterator iBend) :pAbegin(iAbegin), pAend(iAend), pBbegin(iBbegin), pBend(iBend), result(0) { } bool operator==(const DataForHistory& rh) { if (pAbegin == rh.pAbegin && pAend == rh.pAend && pBbegin == rh.pBbegin && pBend == rh.pBend) return true; else return false; } void set(Iterator iAbegin, Iterator iAend, Iterator iBbegin, Iterator iBend) { pAbegin = iAbegin; pAend = iAend; pBbegin = iBbegin; pBend = iBend; } Iterator pAbegin; Iterator pAend; Iterator pBbegin; Iterator pBend; int result;//存储计算的结果 };
自定义查找历史记录函数
上面是一个保存历史记录的结构体,包含四个迭代器和一个与根据四个迭代器计算出来的字符串距离result。下面我自己定义了一个find()函数用于查找即将需要的记录是否在历史记录中:
//查找历史记录中是否存在data template<typename Iterator> int find(vector<DataForHistory<Iterator> >& history, DataForHistory<Iterator>& data) { int k=-1; for (int i=0; i<history.size(); i++) { if (data == history[i]) { k = i; break; } } return k; }
递归决策函数
从而就可以定义一个函数来“决策是否需要递归计算,如果data已经存在就不再递归计算而直接返回历史记录中保存的数据;如果历史记录中找不到,则递归计算出数据,然后push到历史记录中”,实现代码如下:
template<typename Iterator> int findOrCaculate(vector<DataForHistory<Iterator> >& history, Iterator pAbegin, Iterator pAend, Iterator pBbegin, Iterator pBend) { DataForHistory<Iterator> data(pAbegin,pAend,pBbegin,pBend); int i = find(history,data); if (i != -1) // if (false) //不查找历史记录,对每一次需求都重新递归计算 { return history[i].result; } else { data.result = caculateDistance(pAbegin,pAend,pBbegin,pBend); history.push_back(data); //cout << data.pAbegin << ", " << data.pAend << ", " // << data.pBbegin << ", " << data.pBend << ". " //cout << data.result << endl; return data.result; } }
上面代码中有一个注释了的if(false)是用来测试不使用查找历史记录而是每出现一次需要计算的时候直接递归计算时所需的递归次数,我测试的结果如下:
这样一看相差忒大了,所以使用查找数据是很明智的选择(即使查找需要话费时间,但相对于重复进行相同的递归计算还是很不错的)。
PS
上文我使用了自定义的find函数,是由于中途写代码时使用<algorithm>中的find()函数是出现了一大堆的错误,结果没找到错误的原因,模板嘛,一出现错误总是一大堆的。其实到我就找到错误的根源了,错误代码:
template<typename Iterator> int findOrCaculate(vector<DataForHistory<Iterator> >& history, Iterator pAbegin, Iterator pAend, Iterator pBbegin, Iterator pBend) { DataForHistory<Iterator> data(pAbegin,pAend,pBbegin,pBend); vector<DataForHistory<Iterator> >::iterator it = find(history.begin(),history.end(),data); if (it) { return it->result; } else { data.result = caculateDistance(pAbegin,pAend,pBbegin,pBend); history.push_back(data); return data.result; } }
错误提示:
like.cpp:69:2: error: need 'typename' before 'std::vector<DataForHistory<Iterator> >::iterator' beca
use 'std::vector<DataForHistory<Iterator> >' is a dependent scope
所以我就在'std::vector<DataForHistory<Iterator> >::iterator'之前加了typename。(这里不清楚为什么?)
然后继续编译,还有错:
like.cpp:70:2: error: could not convert 'it' from 'std::vector<DataForHistory<__gnu_cxx::__normal_it
erator<char*, std::basic_string<char> > >, std::allocator<DataForHistory<__gnu_cxx::__normal_iterato
r<char*, std::basic_string<char> > > > >::iterator {aka __gnu_cxx::__normal_iterator<DataForHistory<
__gnu_cxx::__normal_iterator<char*, std::basic_string<char> > >*, std::vector<DataForHistory<__gnu_c
xx::__normal_iterator<char*, std::basic_string<char> > >, std::allocator<DataForHistory<__gnu_cxx::_
_normal_iterator<char*, std::basic_string<char> > > > > >}' to 'bool'
看到上面的from ‘xxx’ to ‘bool’了,这下知道了it不是bool型的,怎么判断,需要改为
if (it != history.end())
即找到最后了还是没找到。这样就解决了find函数的问题,就可以不用自己定义专门的find函数了,正确代码如下:
//决策是否递归计算,如果data已经存在就不再递归计算而直接返回历史记录中保存的数据 //如果历史记录中找不到,则递归计算出数据,然后push到历史记录中 template<typename Iterator> int findOrCaculate(vector<DataForHistory<Iterator> >& history, Iterator pAbegin, Iterator pAend, Iterator pBbegin, Iterator pBend) { DataForHistory<Iterator> data(pAbegin,pAend,pBbegin,pBend); typename vector<DataForHistory<Iterator> >::iterator it = find(history.begin(),history.end(),data); if (it != history.end()) { return it->result; } else { data.result = caculateDistance(pAbegin,pAend,pBbegin,pBend); history.push_back(data); return data.result; } }
递归函数
接下来就是怎么写递归函数了,形式上和前面的递归函数差不多,只是把需要继续使用递归函数的时候不是直接调用递归函数,而采用简洁调用。改为调用findOrCaulate()。
template<typename Iterator> int caculateDistance(Iterator pAbegin, Iterator pAend, Iterator pBbegin, Iterator pBend) { static vector<DataForHistory<Iterator> > history; cout << "call caculateDistance() times:"<< history.size() << endl; if (pAbegin>pAend) { if (pBbegin>pBend) return 0; else return pBend-pBbegin+1; } if (pBbegin>pBend) { if (pAbegin>pAend) return 0; else return pAend-pAbegin+1; } if (*pAbegin == *pBbegin) { findOrCaculate(history,pAbegin+1,pAend,pBbegin+1,pBend); } else { int t1,t2,t3; t1 = findOrCaculate(history,pAbegin+1,pAend,pBbegin+2,pBend); t2 = findOrCaculate(history,pAbegin+2,pAend,pBbegin+1,pBend); t3 = findOrCaculate(history,pAbegin+2,pAend,pBbegin+2,pBend); int minValue = t1>t2?t2:t1; minValue = minValue>t3?t3:minValue; return minValue+1; } }
更好的解法
英文原文:http://www.codeproject.com/Articles/13525/Fast-memory-efficient-Levenshtein-algorithm
C++代码实现:
//Levenshtein算法计算两字符串的编辑距离 #include <algorithm> #include <string> #include <iostream> #include <fstream> #include <vector> using namespace std; int Levenshtein(string& s, string& t) { //第一步 int n = s.size(); int m = t.size(); if (0 == n) return m; else if (0 == m) return n; vector<int> v0(m+1); vector<int> v1(m+1); //第二步 for (int i=0; i<=m; i++) v0[i] = i; //第三四步 int cost=0;//编辑代价 for (int i=1; i<=n; i++) { v1[0] = i; for (int j=1; j<=m; j++) { //第五步 if (s[i-1] == t[j-1]) { cost=0; } else { cost=1; } //第六步 int min = v0[j] + 1; int b = v1[j-1] + 1; int c = v0[j-1] + cost; min = min>b?b:min; min = min>c?c:min; v1[j] = min; } copy(v1.begin(),v1.end(),v0.begin()); } //第七步 return v0[m]; } int main() { string s; string t; string str; fstream f("t.c"); getline(f,s,'\1'); f.close(); f.open("tt.c"); getline(f,t,'\1'); f.close(); cout << s << endl; cout << t << endl; cout << Levenshtein(t,s) << endl; }

作者:涵曦(www.hanxi.cc)
出处:hanxi.cnblogs.com
GitHub:github.com/hanxi
Email:im.hanxi@gmail.com
文章版权归本人所有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。
《 Skynet 游戏服务器开发实战》
-
学习地址:
-
优惠推荐码:
2CZ2UA5u -
可以先免费试学前 2 章内容





 浙公网安备 33010602011771号
浙公网安备 33010602011771号