P4196 [CQOI2006]凸多边形 /【模板】半平面交

[CQOI2006]凸多边形 /【模板】半平面交

题目描述

逆时针给出n个凸多边形的顶点坐标，求它们交的面积。例如n=2时，两个凸多边形如下图：

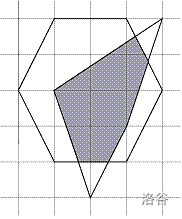
则相交部分的面积为5.233。

输入格式

第一行有一个整数n，表示凸多边形的个数，以下依次描述各个多边形。第i个多边形的第一行包含一个整数mi，表示多边形的边数，以下mi行每行两个整数，逆时针给出各个顶点的坐标。

输出格式

输出文件仅包含一个实数，表示相交部分的面积，保留三位小数。

样例 #1

样例输入 #1

样例输出 #1

5.233

提示

100%的数据满足：2<=n<=10，3<=mi<=50，每维坐标为[-1000,1000]内的整数

Solution

半平面交的模板题。

首先将给出的多边形从顶点转化为边所在直线所划分成为的半平面交（划分后用到的半平面统一取左侧）。直线用一个端点加一个向量进行表示。

为了方便代码的理解，这里先将向量和直线的结构体定义写出：

const int _SIZEP=50,_SIZEF=10;
struct VEC{
	double x,y;
	double operator^(const VEC &a) const {return x*a.y-y*a.x;}//叉乘
	VEC operator*(const double &a) const {return (VEC){x*a,y*a};}//数乘
	VEC operator+(const VEC &a) const {return (VEC){x+a.x,y+a.y};}//向量加
	VEC operator-(const VEC &a) const {return (VEC){x-a.x,y-a.y};}//向量减
}point[_SIZEP+5];
struct LINE{
	VEC p,l;//p表示直线上一点，l是方向的向量
	double k;//k表示向量的极角，在算法实现的时候会用到
	LINE(VEC P,VEC L):p(P),l(L){k=atan2(l.y,l.x);}//atan2(y,x)返回 arctan(y/x)
	LINE(){}
}line[(_SIZEP*_SIZEF)+5];

转化多边形 & 读入：

read(n);
for (int i=1;i<=n;i++)
{
	read(m);
	for (int j=1;j<=m;j++) read(point[j].x),read(point[j].y);
	for (int j=1;j<=m;j++) line[++tot]=LINE(point[j],point[j%m+1]-point[j]);//j%m+1意思是j到了m后+1变成1
}

先来讨论直线的交点如何计算（图片引用自oi-wiki）

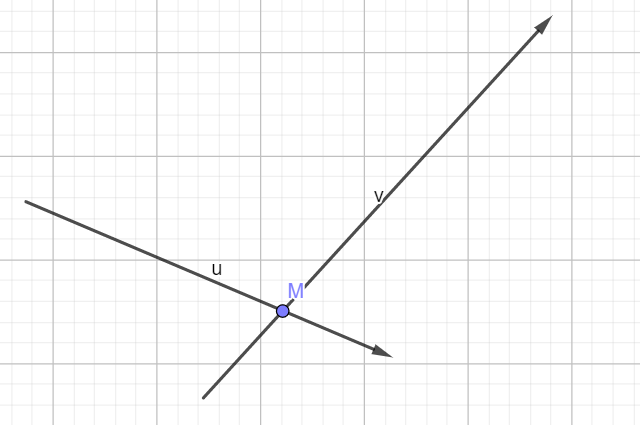
假设直线 \(v\) 上的两个点为 \(A,B\)，\(u\) 上的两个点 \(C,D\)，那么 \(\displaystyle \overrightarrow{AM}=\frac{\overrightarrow{CD}\times \overrightarrow{AC}}{\overrightarrow{AB}\times\overrightarrow{CD}}\cdot \overrightarrow{AB}\)（利用叉乘的几何意义可以算出这个关系），然后可以得知 \(M=A+\overrightarrow{AM}\)。代码实现如下（本篇题解代码中的所有向量叉乘被重载到了^上，*表示向量数乘，+ -分别表示向量加减）：

VEC getP(LINE x,LINE y)
{
	VEC c=x.p-y.p;//向量AC
	double t=(y.l^c)/(x.l^y.l);//参照上面的解释
	return x.p+x.l*t;//计算交点
}

接着来看如何来看知道了直线以及直线交点该如何计算半平面交。

考虑先将所有的直线按照极角排序，那么此时如果依次遍历直线会发现相邻直线直接一定是向左转，将会方便我们之后的处理。

bool cmp(LINE x,LINE y) {return x.k<y.k;}
//main()中
sort(line+1,line+tot+1,cmp);

先将第一、二条直线加入，此时需要存储下这两条直线的交点。现在讨论加入第三条直线的情况：

第三条直线保留的半平面包含了一二条直线的交点

这种情况下，直接将第三条直线加入即可，并且存储下第二条和第三条直线的交点。
第三条直线保留的半平面不包含一二条直线的交点

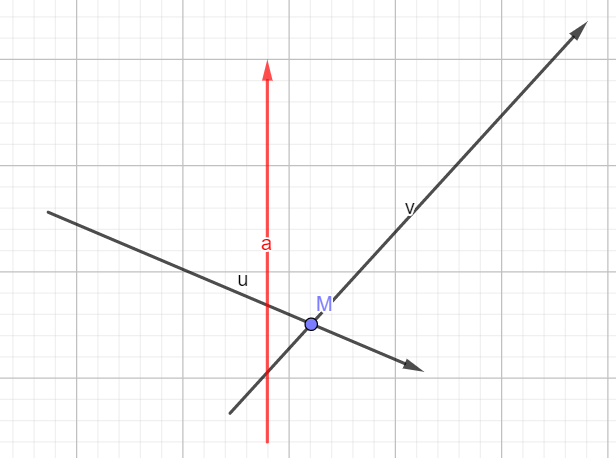
原有直线为 \(u,v\)，新加入直线为 \(a\)，此时交点 \(M\) 已经不在答案的半平面内了，所以需要被踢出，同时被踢出的还有构成这个交点的直线 \(v\)。

这样一来，我们就大概清楚了需要维护的东西。根据上述过程，发现可能会用到栈来进行维护，第一种情况是直接将直线和交点加入栈，第二种情况则判断栈顶是否需要被弹出，一直弹到交点在半平面内才结束并加入栈。

那么半平面交的问题就这么轻松地解决了？并不是，因为在加入直线到后面的时候，可能会出现非常后面的直线保留的半平面把第一二条直线的交点给踢出去的情况：

回到我们维护的栈上面，会发现这一操作需要弹掉栈底的元素，这显然不是栈的操作内容了，而是双端队列。

这样我们就得到了正确的算法：维护一个双端队列，加入新直线的时候把双端队列尾和头中所有不合法的直线连带着交点一起踢出，最后留下的交点就是最终的半平面交多边形的定点。

需要注意的是在加入最后一条直线后，可能会出现队列头的直线能够将队列尾的交点弹出的情况，所以枚举完直线后需要再尝试将队列尾给弹出到合法。

LINE q[1105];int head=1,tail=1;//q用来记录直线
VEC P[1105];//P用来记录交点
void calcP()
{
	q[head]=line[1];//第一条直线直接加入队列
	for (int i=2;i<=tot;i++)
	{
		while (head<tail && (line[i].l^(P[tail-1]-line[i].p))<=eps) tail--;//弹队尾
		while (head<tail && (line[i].l^(P[head]-line[i].p))<=eps) head++;//弹队头
		q[++tail]=line[i];//加入队列
		if (fabs(q[tail].l^q[tail-1].l)<=eps)//判断平行
		{
			tail--;
			if ((q[tail].l^(line[i].p-q[tail].p))>eps) q[tail]=line[i];//留下离可行域更近的那组直线
		}
		if (head<tail) P[tail-1]=getP(q[tail-1],q[tail]);//计算交点（如果队列里面有两条线的话）
	}
	while (head<tail && (q[head].l^(P[tail-1]-q[head].p))<=eps) --tail;//弹队尾重复的
	if (tail-head<=1) return;
	P[tail]=getP(q[head],q[tail]);//算队尾和队头的交点
}

算完半平面交的顶点后，这道题还需要求出半平面交的面积。这用向量叉积可以快速求出（因为向量叉积是有向面积，在图形外的部分正负计算次数相等，相互抵消，只留下了图形内部面积）。具体做法就是平面上随便取一个点 \(O\)，然后连接点 \(O\) 和图形的顶点得到数量等于顶点数的向量，接着将相邻向量做叉积，最后全部相加就是多边形的面积。代码实现的时候可以把点 \(O\) 看做原点，这样多边形顶点的坐标就是上述的向量。

double ans=0;
void calcS()
{
	for (int i=head;i<=tail;i++)
		ans+=P[i]^(P[(i+1>tail)?head:i+1]);//特判最后一个点的情况，因为它是和1一起算的
}
//main()中
printf("%.3lf\n",ans/2);

最后放上完整代码：

Code

~~上面注释够详细了所以这里就不写了（~~

#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof a)
using namespace std;
template<typename T> void read(T &k)
{
	k=0;T flag=1;char b=getchar();
	while (!isdigit(b)) {flag=(b=='-')?-1:1;b=getchar();}
	while (isdigit(b)) {k=k*10+b-48;b=getchar();}
	k*=flag;
}
const double eps=1e-8;
const int _SIZEP=50,_SIZEF=10;
struct VEC{
	double x,y;
	double operator^(const VEC &a) const {return x*a.y-y*a.x;}//cross
	VEC operator*(const double &a) const {return (VEC){x*a,y*a};}//point
	VEC operator+(const VEC &a) const {return (VEC){x+a.x,y+a.y};}//vec plus
	VEC operator-(const VEC &a) const {return (VEC){x-a.x,y-a.y};}//vec minus
}point[_SIZEP+5];
struct LINE{
	VEC p,l;
	double k;
	LINE(VEC P,VEC L):p(P),l(L){k=atan2(l.y,l.x);}
	LINE(){}
}line[(_SIZEP*_SIZEF)+5];
int tot;
bool cmp(LINE x,LINE y) {return x.k<y.k;}
VEC getP(LINE x,LINE y)
{
	VEC c=x.p-y.p;
	double t=(y.l^c)/(x.l^y.l);
	return x.p+x.l*t;
}
LINE q[1105];int head=1,tail=1;
VEC P[1105];
void calcP()
{
	q[head]=line[1];
	for (int i=2;i<=tot;i++)
	{
		while (head<tail && (line[i].l^(P[tail-1]-line[i].p))<=eps) tail--;
		while (head<tail && (line[i].l^(P[head]-line[i].p))<=eps) head++;
		q[++tail]=line[i];
		if (fabs(q[tail].l^q[tail-1].l)<=eps)
		{
			tail--;
			if ((q[tail].l^(line[i].p-q[tail].p))>eps) q[tail]=line[i];
		}
		if (head<tail) P[tail-1]=getP(q[tail-1],q[tail]);
	}
	while (head<tail && (q[head].l^(P[tail-1]-q[head].p))<=eps) --tail;
	if (tail-head<=1) return;
	P[tail]=getP(q[head],q[tail]);
}
double ans=0;
void calcS()
{
	for (int i=head;i<=tail;i++)
		ans+=P[i]^(P[(i+1>tail)?head:i+1]);
}
int n,m;
int main()
{
	read(n);
	for (int i=1;i<=n;i++)
	{
		read(m);
		for (int j=1;j<=m;j++) read(point[j].x),read(point[j].y);
		for (int j=1;j<=m;j++) line[++tot]=LINE(point[j],point[j%m+1]-point[j]);
	}
	sort(line+1,line+tot+1,cmp);
	calcP();
	calcS();
	printf("%.3lf\n",ans/2);
	return 0;
}

posted @ 2022-08-12 17:06 Hanx16Msgr 阅读(92) 评论(0) 收藏举报

刷新页面返回顶部

一个蒟蒻的学习笔记

欢迎神犇！！！