点云矩阵变换

转载：https://blog.csdn.net/weixin_42783619/article/details/116952488

• 变换矩阵工作原理 :

|-------> 变换矩阵列
| 1 0 0 x | \
| 0 1 0 y | }-> 左边是一个3阶的单位阵(无旋转)
| 0 0 1 z | /
| 0 0 0 1 | -> 这一行用不到 (这一行保持 0,0,0,1)

要进行点云旋转，需要对3阶矩阵进行赋值
如何赋值参考：https://blog.csdn.net/weixin_39637723/article/details/111686018
pcl中使用参考：https://blog.csdn.net/weixin_38275649/article/details/80968364

• 世界坐标系与相机坐标系转换

世界坐标系与相机坐标系转换是一样的，如下是X由世界坐标转换到相机坐标系，并由内参矩阵K变换到图像坐标（这里X是列向量）

内参矩阵K：

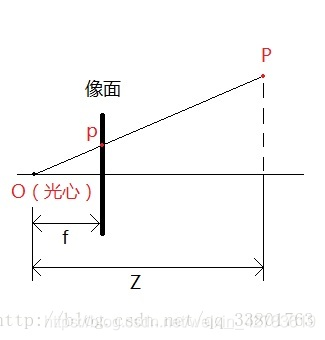
内参外参、世界坐标系与相机坐标系转换：https://blog.csdn.net/qq_33801763/article/details/77033064

• 旋转变换实现

参考：https://blog.csdn.net/weixin_42783619/article/details/116478710

• 变换矩阵（Translation Matrix）

如果我们需要表示一个3D空间的平移，那得需要一个4*4的矩阵。首先，我们预定义坐标向量都是列的形式，如果是行的形式，要先进行转置变换。

旋转平移矩阵的形式如下：

其中Transform_XAxis是新坐标系下的x轴的方向，Transform_YAxis是新坐标系下的y轴的方向，其中Transform_ZAxis是新坐标系下的z轴的方向。Translation 描述了新空间相对于活动空间的位置

某些情况下，我们需要简单的变换，类似平移和旋转。

• Translation 平移

     

     其中translation是一个3D的向量，代表我们想要移动空间的位置。

• 尺度矩阵（Scale Matrix）

     

      这个比较好理解。scale是一个3D向量，表示每个轴的缩放尺度。

• 旋转矩阵（Rotation Matrix）

       绕x轴旋转θ：

       

       绕y轴旋转：

       

      绕z轴旋转：

      

参考：https://52zju.cn/?p=580
其他参考：https://zhuanlan.zhihu.com/p/147282442
旋转矩阵变换的乘积顺序问题：https://blog.csdn.net/potato_uncle/article/details/110096514
两个旋转矩阵（Rotation Matrix）相乘（Multiply）的几何意义：https://dawnarc.com/2017/02/math两个旋转矩阵rotation-matrix相乘multiply的几何意义/
实现参考：https://www.learnopencv.com/rotation-matrix-to-euler-angles/
https://blog.csdn.net/reasonyuanrobot/article/details/89969676
https://blog.csdn.net/u011808673/article/details/93970439
————————————————
版权声明：本文为CSDN博主「BLACKVEIL」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/weixin_42783619/article/details/116952488