着色(Shading)
(1)着色(Shading)
有些地方亮些,有些地方暗些,有些地方有颜色,有些地方没颜色。我们给它的定义是给不同物体应用不同材质的过程。
最简单的着色模型:Blinn-Phong 反射模型。
下图分别表示高光、漫反射和环境光照(间接光照)。

我们现在考虑光照是考虑任何一个点上,即 shading point 这个点它的着色结果是多少。定义观察方向 v、法线 n、光照方向 l。既然定义的都是方向,那么这些向量都是单位向量。
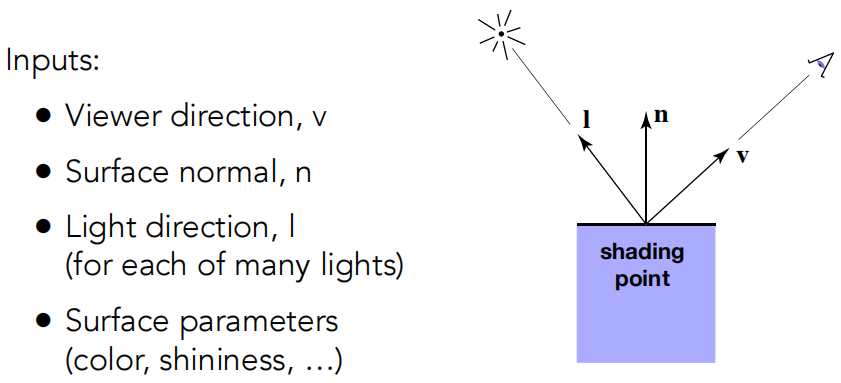
着色跟阴影没关系,我们不考虑这个点是不是在阴影内,我们只看这个点跟光照和观察角度的关系,不考虑其他物体的存在,是局部发生的事情。着色和材质没什么区别,不同的材质对应着不同的着色。

(2)漫反射(Lambertian (Diffuse) Shading)
一束光线打到一个物体表面某一点,光线会被均匀地反射到各个不同的方向。
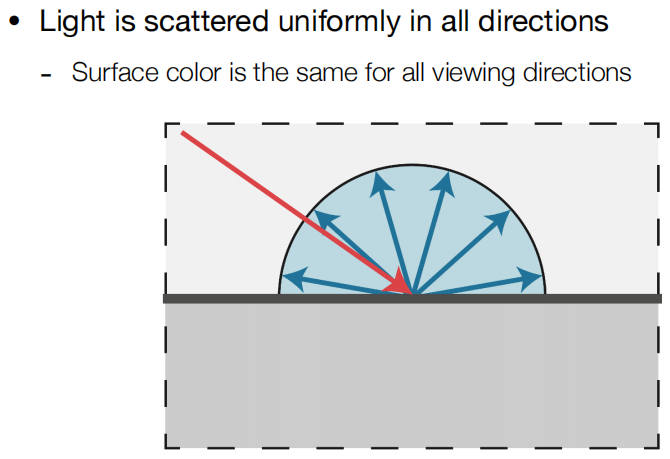
之前的图像也可以看到,同样的光以不同的角度照上去,得到的明暗是不一样的。这是为什么呢?
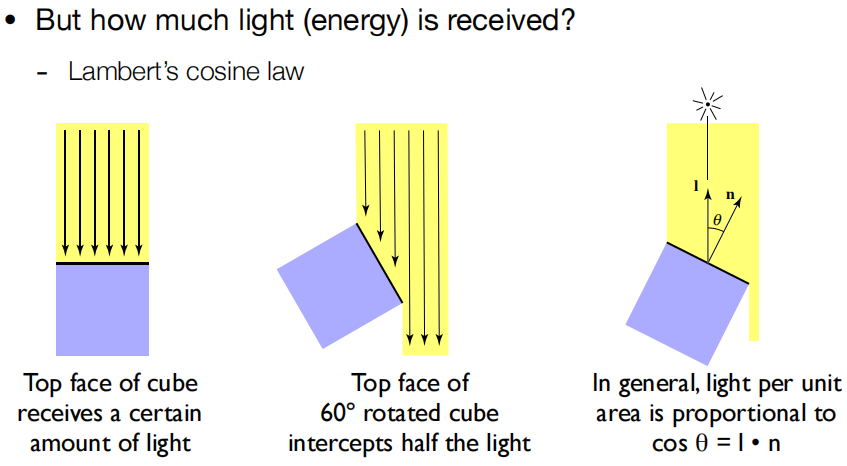
假如光是离散的,我可以用一根根光线来表示照射,每一根光线代表了固定的能量。第一幅图物体表面与光线垂直,可以接收到所有的 6 根光线,而第二幅图转动了 60° 就只能接收到 3 根光线了,也就是说,这时候物体表面就应该暗一点。推广到任意角度就得到右边的方程,Lambert 余弦定律。
也可以联想到我们地球上为什么有四季之分,也是因为阳光的直射的角度不同,当南半球是夏天的时候北半球是冬天。
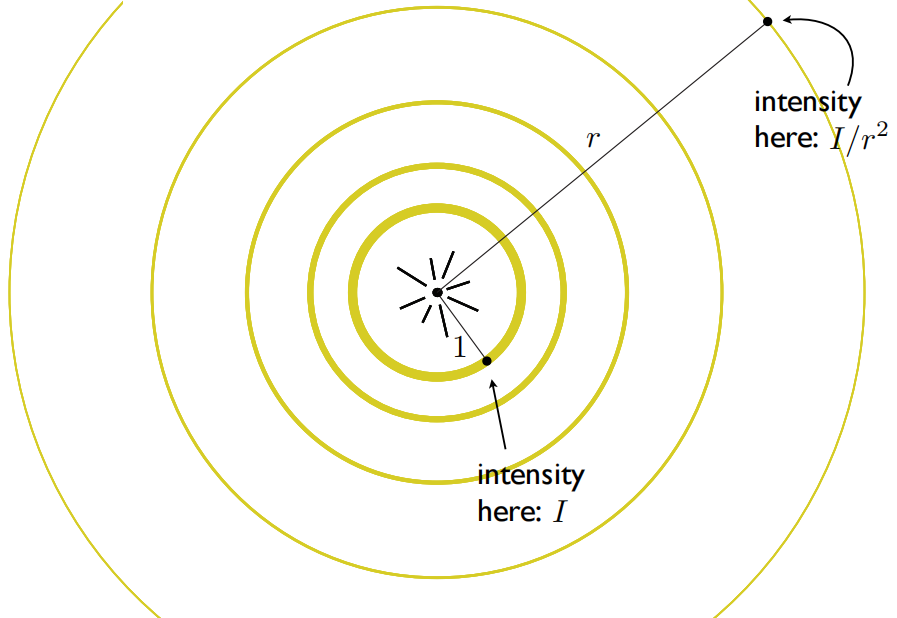
点光源光照的衰减。当距离点光源距离是 1 的时候,定义光的强度为 I,当它传播到距离是 r 的时候,光强为 I / r2。
假设我们知道了一个点光源,然后我们又知道 shading point 离点光源有多远,那我们就知道有多少的光传播到 shading point 附近。我们又知道有多少的光会被 shading point 吸收,那我们结合起来,就知道最后漫反射(Diffuse)能看到多少明暗了。
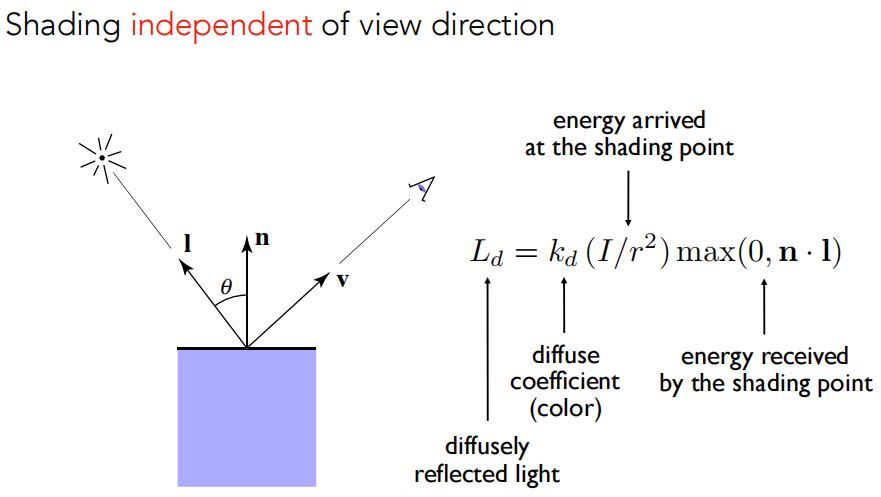
为什么有个 max(0, n*l),因为两个向量点乘如果小于零,我们就认为没有什么物理意义,光线穿过物体表面,打到下面的材质,这里也没有折射的什么事,所以直接令其为 0。
系数 kd 表示有多少光线被物体表面给吸收了,即反射率,如果 kd=0,光线打到物体表面所有光线都被吸收了,没有能量反射出去,那就是黑色了。
在漫反射下,与观测的方向 v 完全没有关系,你从任何角度上看这个着色点都是一样的明暗,从右边的式子上也是如此。

(3)高光(Specular Term)
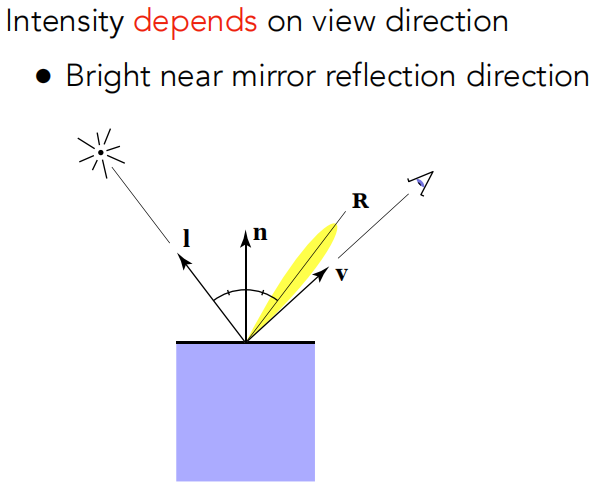
经验性的观察,当我观察的方向与镜面反射的方向接近的时候能看到高光,其他时候我都看不到高光。
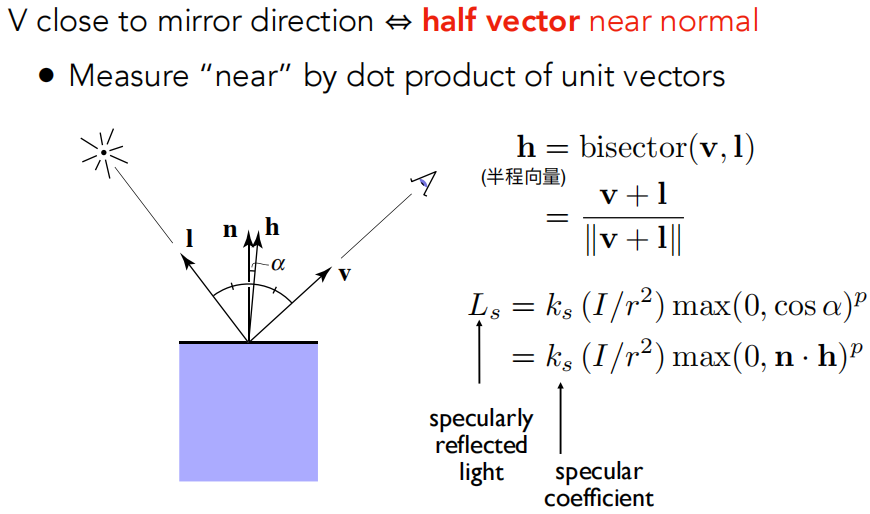
法线方向与半程向量方向,即法线方向与 l 和 v 的角平分线方向很接近时能看到高光。而向量的角平分线就很好求出,直接向量相加即可。向量 n 和向量 h 相乘,如果接近 1 则说明接近。ks 镜面反射系数。
注意到这里没有考虑 kd,没有考虑多少能量被吸收了。实际如果严格考虑的话确实要考虑反射率,这里没有考虑是因为 Blinn-Phong 模型毕竟是经验性模型,把这一项简化掉了,我们考虑的更多的还是在某些方向上是否能看见高光。
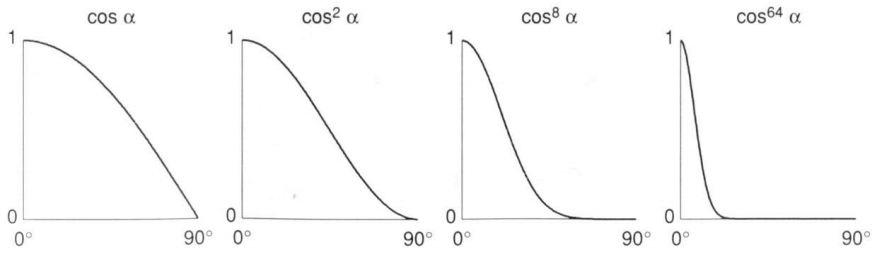
这里有个指数 p,因为向量之间夹角余弦确实能体现两个向量是不是足够接近,但它的容忍度太高了,像第一幅图,到 45° 时我已经认为离得挺远了,但它的值还是不低。我们平常看到的高光还是非常亮,集中在一个很小的区域内,这就说明这两个方向只要离得稍微远一点我就看不到高光了。于是加个指数 p 就非常合理了,一般在 Blinn-Phong 模型中 p 会取到 100 到 200 的值。

(4)环境光照(Ambient Term)
来自各种各样的光反射无数多次后再对某个地方做出影响,来自环境的光是一个多么复杂的东西,那么我们可以做一个大胆的假设,任何一个点接收到来自环境中的光永远都是相同的,而它的强度叫做 Ia;ka 是环境光的一个系数。实际上当然不是这么回事,实际上如果我们想很精确地计算它,就要用到全局光照的知识。

下面就是 Blinn-Phong 着色模型的效果:

(5)着色频率
这三个球有完全相同的几何表示,从球的边界也能看出来。那为什么着色了之后结果各不相同呢?

着色频率就是说我要把这些着色应用在哪些点上。比如第一幅图我把着色应用在一个面上,那么一个面有一个固定的法线,求出它的 shading 的结果是多少,那么它整个平面都这个颜色,也就是说一个平面我只能做一次 shading;第二幅图则是对多边形每个顶点都算出法线,每个顶点都做一次着色,然后再用插值的方法进行着色;第三幅图则是应用在每一个像素上,所以得到一个非常好的结果。
接下来对这三种方法做一个正规的定义:
(1)Shade each triangle (flflat shading)

(2)Shade each vertex (Gouraud shading)

(3)Shade each pixel (Phong shading)

三种着色频率的比较:

当几何形状数量够多的时候其实就可以选择一些计算量较少的着色频率,效果一样很好。
但如果逐顶点着色,那法线怎么计算呢?
如果原本表示的是球,那当然好计算,直接拿球心来计算法线,但现实中更多的是不规则的形状。
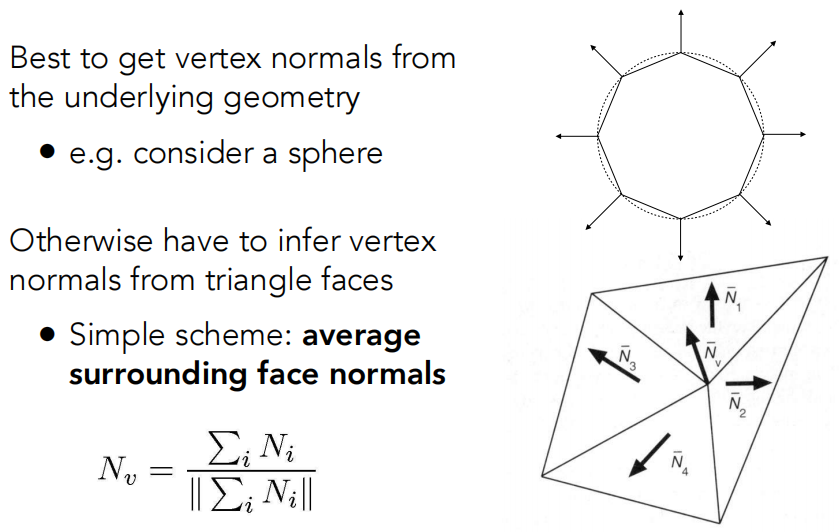
那就将顶点的法线认为是它相邻面的法线求平均就可以了,直到现在还是为大家所用。并且如果对每个面我设法进行加权,效果也会更好。
那么逐像素的法线呢?
拿顶点的法线进行插值即可。那具体怎么插值呢?需要用到重心坐标。后面会讲。
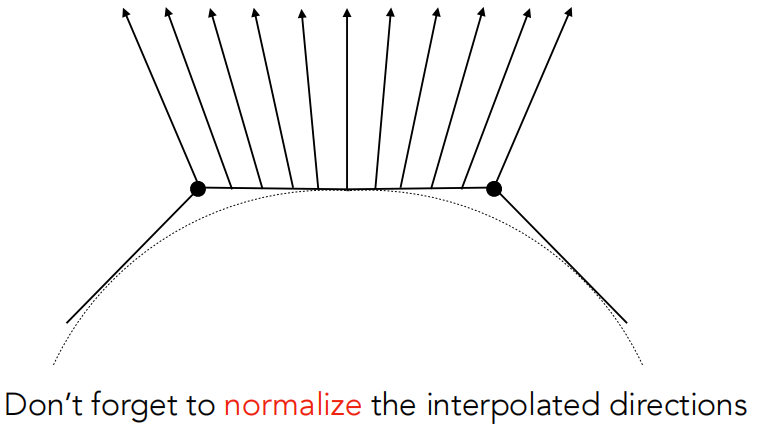
记得所有的法线都是方向,所以都要进行归一化,把它变成单位向量。
(6)重心坐标

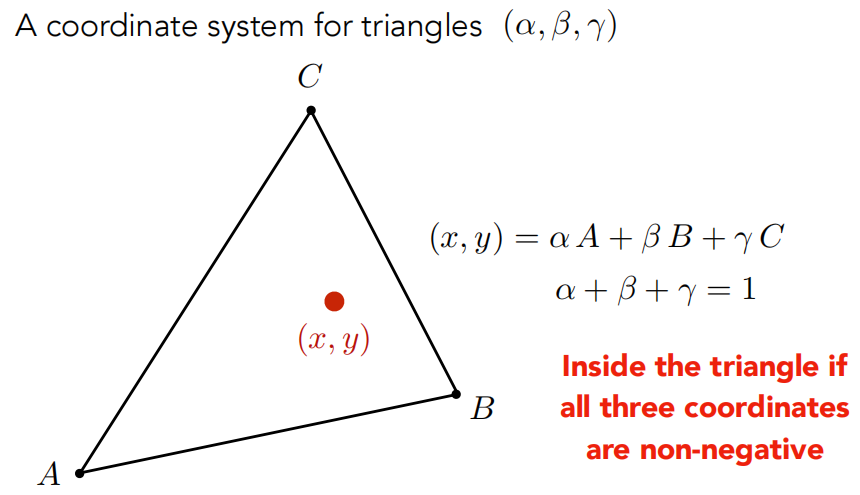
重心坐标告诉我们,在三角形 ABC 所在平面内任何一点 (x, y) 都可以表示成,三个顶点 A、B、C 它们坐标的线性组合。(α, β, γ) 用来描述一个点 (x, y)。且实际上中心坐标虽然是三个数,但知道两个数就马上能知道第三个数。α + β + γ 如果不等于 1,那么这个点不在三角形所在平面内。
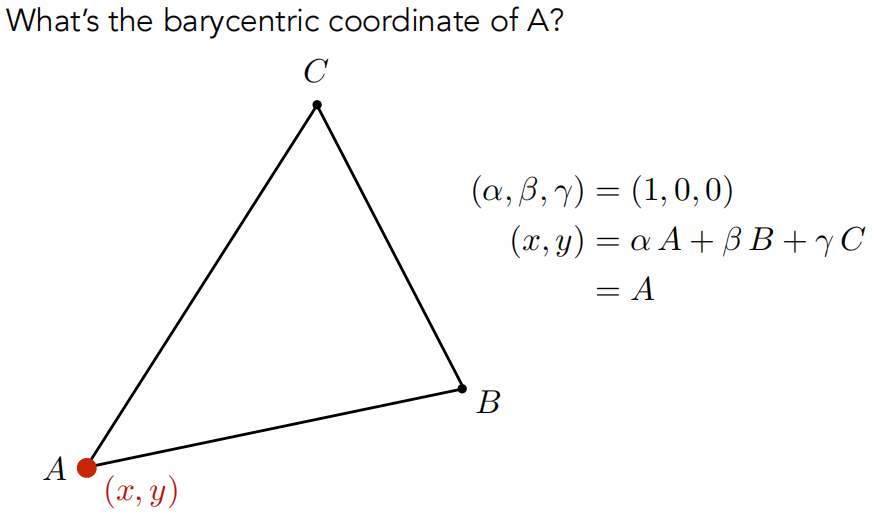
A 点所在的重心坐标为:
任意一个点的重心坐标可以通过面积比求出:
如 A 点的对面有个三角形 AA,这是 A 点对应的三角形。知道两个顶点和任意一个点的坐标,根据向量求出面积当然很容易求出。
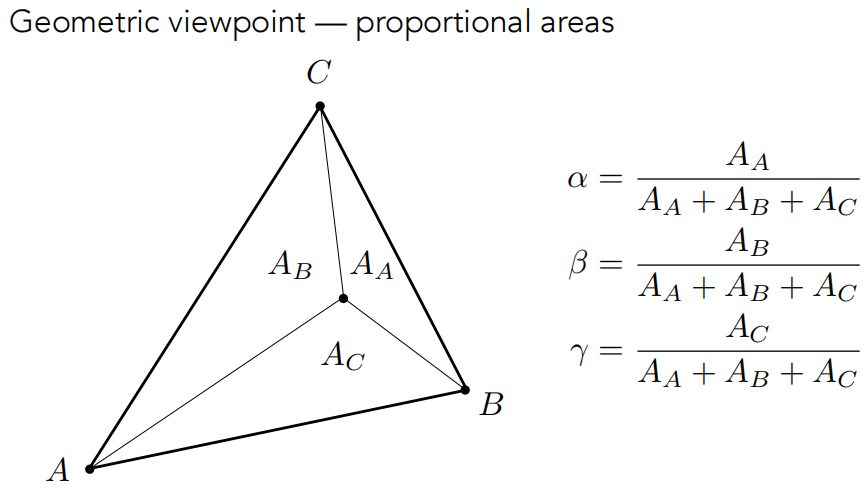
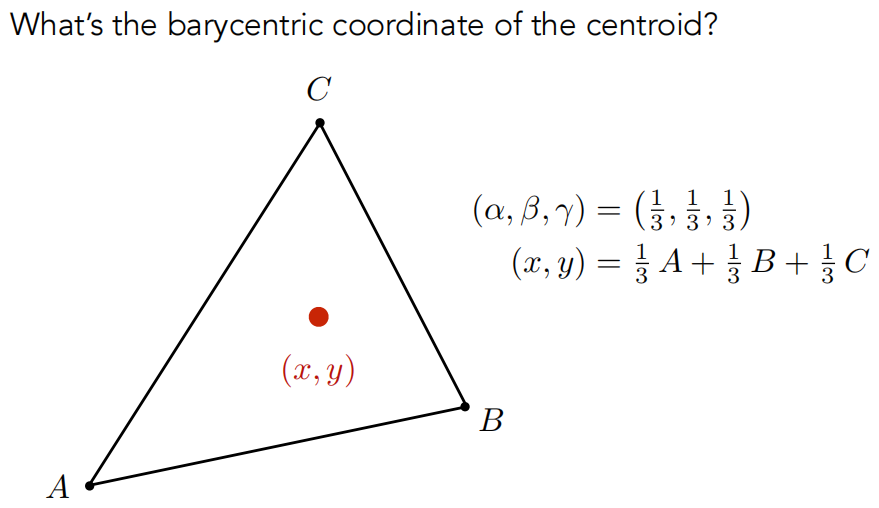
从这种定义方法,可以得出一个特殊的点的重心坐标,即三角形自己的重心,它把三角形的面积均等地分成了三份。
简化的计算方法:
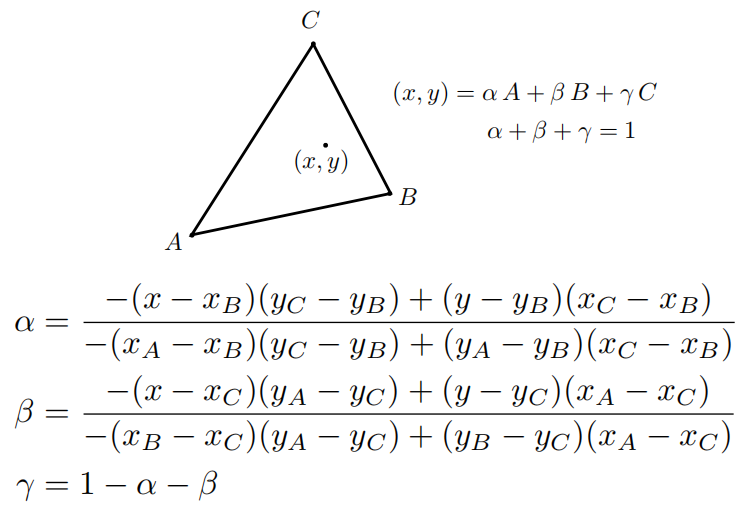
如果我要做插值,那么我要插值的属性同样应该用重心坐标将它们线性组合起来。
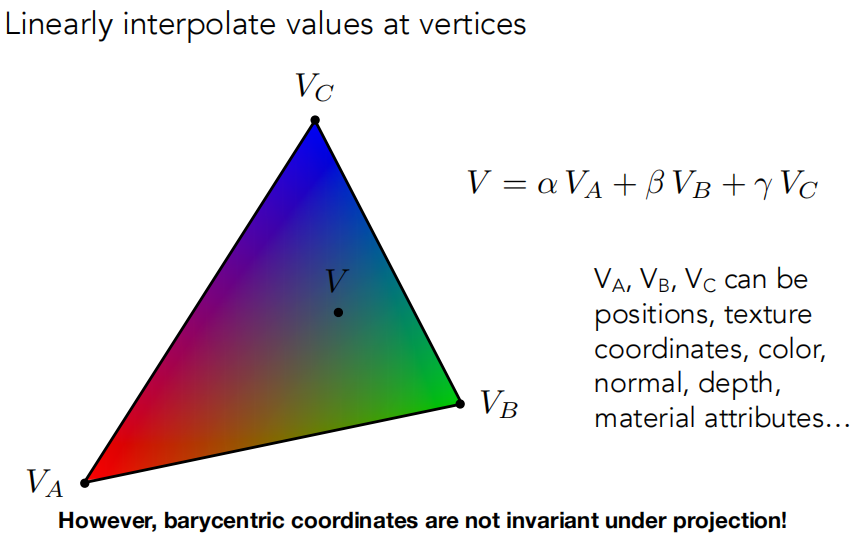
重心坐标虽然简单方便快捷,但是在投影变换下,是不能保证重心坐标不变的。因为经过近大远小的透视变化,原本面积相等的三角形也变得不相等了。
这个事情告诉我们,如果我们想插值一些三维空间中的属性,就应该取三维空间中的坐标来计算重心坐标,然后再做插值,而不能在投影变换之后的三角形内做插值。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号