【邪修】一起用CTF Crypto技能包破解这道高中钓鱼题!
引言
视频封面:

这几天笔者终于装好了SageMath,刚好虐一道有名的高中钓鱼题助助兴~
已知 $x2+y2=1$ ,求 $(x+1)(y+2)$ 最大值
如果把目标函数改成 $(x+1)(5y+2)$ ,这题就是道高中常规题。但为什么目标函数加了系数,问题反而变简单了呢?
本文大纲:
- 为什么 $(x+1)(5y+2)$ 可以求, $(x+1)(y+2)$ 就求不出?
- 拉格朗日乘数法简介
- Gröbner基极粗略介绍(高中生也能看)
- 用
SageMath轻松求钓鱼题的解析解
我们会用高中生也能轻松听懂的语言讲解本文用到的高等数学工具:拉格朗日乘数法和Gröbner基。然后我们会用SageMath写代码,轻松求出这题的解析解。
本文 52pojie: https://www.52pojie.cn/thread-2085192-1-1.html
本文 博客园: https://www.cnblogs.com/hans77/articles/19458128
本文 juejin: https://juejin.cn/post/7592816646869860361
作者:hans774882968以及hans774882968以及hans774882968以及hans77
为什么 $(x+1)(5y+2)$ 可以求, $(x+1)(y+2)$ 就求不出?
三角换元+万能公式:设 $x=\frac{1-t2}{1+t2},\ y=\frac{2t}{1+t^2}$ ,则 $(x+1)(5y+2) = (\frac{1 - t^2}{1 + t^2} + 1)(5 \cdot \frac{2t}{1 + t^2} + 2) = \frac{2}{1 + t^2} \cdot \frac{2t^2 + 10t + 2}{1 + t^2} = \frac{2(2t^2 + 10t + 2)}{(1 + t2)2} = \frac{4t^2 + 20t + 4}{(1 + t2)2}$
常规动作,对这个分式函数求导(分母是正的,仅展示分子):
$$
(8t + 20)(1 + t2)2 - (4t^2 + 20t + 4) \cdot 4t(1 + t2)=(1+t2)(2t^3 + 15t^2 + 2t - 5)(-4)
$$
令 $2t^3 + 15t^2 + 2t - 5=0$ ,发现可以试根得到其中一个根 $t=\frac{1}{2}$ ,于是可以进行多项式除法 $\frac{2t^3 + 15t^2 + 2t - 5}{2t-1}=t^2 + 8t + 5$ ,于是得到另外两个极值点 $t = -4 \pm \sqrt{11}$
我们看导数的分子的图像,不难想象原分式函数的图像。
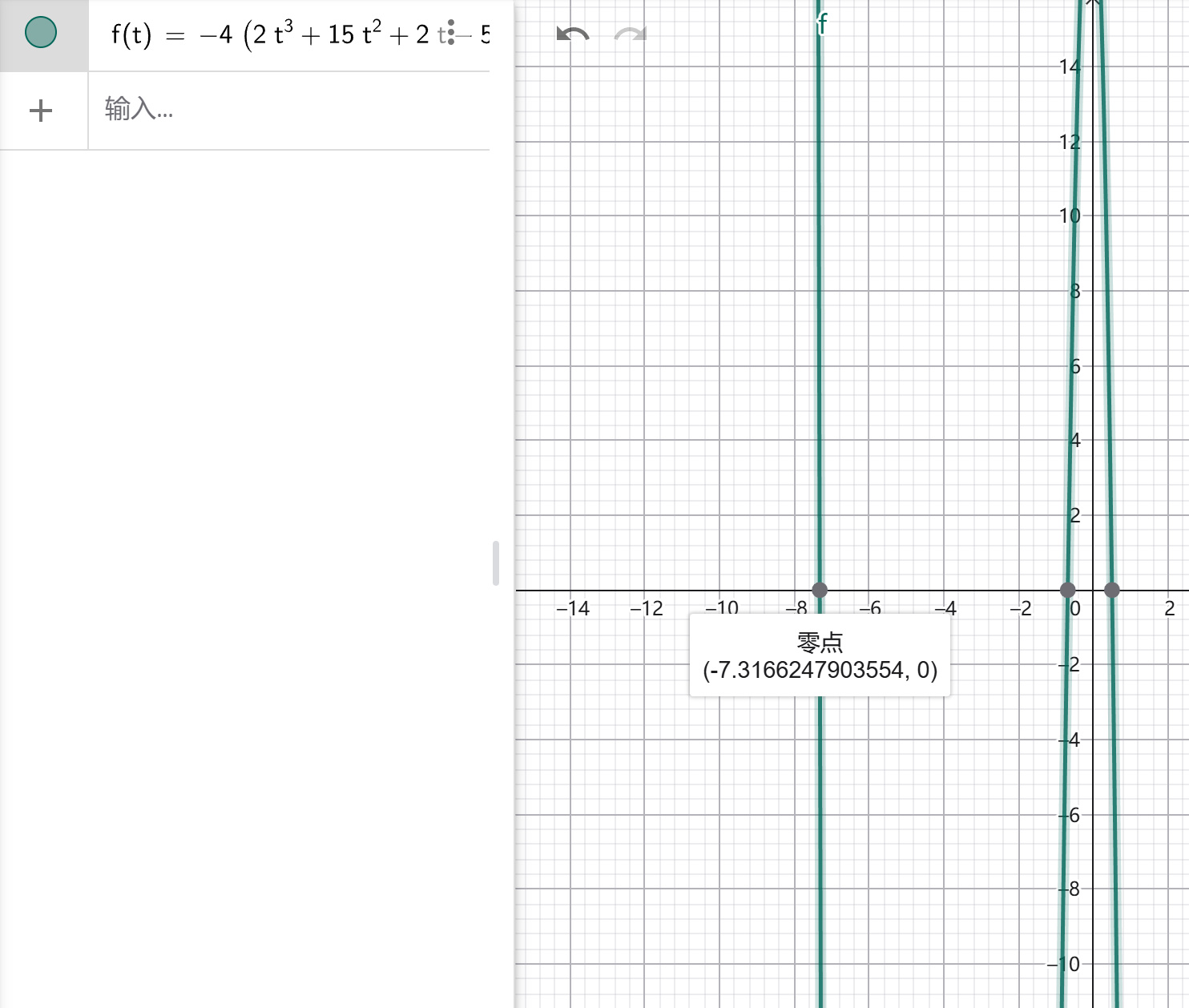
发现只需要对比 $t=-4-\sqrt{ 11 }$ 和 $t=\frac{1}{2}$ 处函数值的大小。对比发现 $t=\frac{1}{2}$ 时函数取得最大值 $\frac{48}{5}$ ,此时 $x=\frac{3}{5},\ y=\frac{4}{5}$
同样对 $(x+1)(y+2)$ 用三角换元+万能公式: $(x+1)(y+2)=(\frac{1 - t^2}{1 + t^2} + 1)(\frac{2t}{1 + t^2} + 2)=\frac{4t^2 + 4t + 4}{(1 + t2)2}$
对这个分式函数求导(仅展示分子):
$$
(8t + 4)(1 + t2)2 - (4t^2 + 4t + 4) \cdot 4t(1 + t^2)=(1 + t^2) \cdot (-4)(2t^3 + 3t^2 + 2t - 1)
$$
这个函数在R上只有一个根,而且它不能试出来。实际上,这道钓鱼题的做法有很多,但多尝试几种不同做法后会发现:无论什么做法,最后都必须解一个很难解的3次方程,命题人需要精心挑选系数,来让这个3次方程的解能够手算得到,才能出一道类似的高考模拟题。绝大多数情况下,都无法手算求解这种问题,需要考虑写代码。
拉格朗日乘数法简介
已知 $x2+y2=1$ ,求 $(x+1)(y+2)$ 最大值
这类问题在微积分里属于条件极值问题,其中 $x2+y2=1\ (\phi(x,y)=x2+y2-1=0)$ 叫约束条件(约束方程), $f(x,y)=(x+1)(y+2)$ 叫目标函数。
我们以两个变量x、y、两个约束条件 $\phi_{1}(x,y)=0,\ \phi_{2}(x,y)=0$ ,目标函数 $f(x,y)$ 为例。为了解决这类问题,我们构造拉格朗日函数 $F(x,y,\lambda_{1},\lambda_{2})=f(x,y)+\lambda_{1}\phi_{1}(x,y)+\lambda_{2}\phi_{2}(x,y)$ 。令它对每一个变量的偏导都等于0:
$$
\begin{cases}
\frac{\partial F}{\partial x}=0 \
\frac{\partial F}{\partial y}=0 \
\frac{\partial F}{\partial \lambda_{1}}=\phi_{1}(x,y)=0 \
\frac{\partial F}{\partial \lambda_{2}}=\phi_{2}(x,y)=0
\end{cases}
$$
这样解出的x、y一般都包含所有的极值点,但也可能包含一些驻点。对于某些特殊的函数和约束,拉格朗日乘数法可能会漏掉极值点。本文不涉及这些刁钻的情况,读了大学再慢慢接触吧
接下来我们用拉格朗日乘数法处理下这道钓鱼题。构造拉格朗日函数 $F(x,y,\lambda)=(x+1)(y+2)+\lambda(x2+y2-1)$ ,令它对每一个变量的偏导都等于0:
$$
\begin{cases}
2\lambda x + y + 2 = 0 \
2\lambda y + x + 1 = 0 \
x^2 + y^2 = 1
\end{cases}
$$
写代码求这个方程组的数值解很简单。但为了求解析解,我们需要先完成消元。实际上,前面讲的三角换元+万能公式就是其中一种手算消元方法。
SageMath可以轻松求这个方程组的数值解:
x, y, t = var('x y t')
sols = solve([2 * t * x + y + 2, 2 * t * y + x + 1, x ^ 2 + y ^ 2 - 1])
print(sols) # 我们想要的: [y == 0.576378809869376, x == 0.8171826341820846, t == -1.576378721327477] ,排除一个y=0,以及两个复数根
Gröbner基极粗略介绍(高中生也能看)
接下来非常粗略地介绍Gröbner基。这是代数几何的一个工具,学习难度对高中生来说很大,但幸好这期视频只需要对它建立一个感性印象。
$$
\begin{cases}
2\lambda x + y + 2 = 0 \
2\lambda y + x + 1 = 0 \
x^2 + y^2 = 1
\end{cases}
$$
我们观察上一页得到的方程组,发现它的每一项都只含有 $kxayb, a \geq 0,\ b \geq 0$ 。我们把这些项叫做“单项式”,单项式加起来就叫多元多项式
接下来我们回顾一下线性方程组是怎么解的。比如:
$$
\begin{cases}
2x + 3y = 5 \
x - y = 1
\end{cases}
$$
用高斯消元法把它变成“上三角”形式:
$$
\begin{cases}
x - y = 1 \
\quad\quad 5y = 3
\end{cases}
$$
这里第二条式子已经消去了x,是单变量方程。我们希望多元多项式方程组也能完成类似的消元过程——Gröbner基就能做这件事。
类比Gröbner基和线性空间的基
为了看懂代码,我们需要类比Gröbner基和线性空间的基。这里会涉及一些简单的线性代数,但没关系,我们只需要建立感性印象,足够看懂代码就行~
我们在高中学过平面向量和空间向量。在平面里,我们通常用 $(1,0),\ (0,1)$ 这两个向量表示平面内所有向量,我们说这两个向量是2维线性空间的一组基,也可以说这组基生成了2维线性空间。为什么用单位向量呢?其他向量不行吗?实际上,任意两个不共线的向量都可以表示平面内所有向量,比如 $(11,45),\ (14,11)$ 不共线,也可以是一组基。但它的性质没有单位向量“好”,用起来不方便!
给定一组向量 $v_{1},v_{2},\dots,v_{k}$ ,里面可能有一些向量是能够用其他向量线性表出的,把这些多余的向量去掉,剩下的向量两两线性无关,我们就说它们是一组基。比如,给定 $(11,45),\ (14,11),\ (25,56)$ ,我们发现 $v_{3}=v_{1}+v_{2}$ ,所以 $v_{3}$ 是多余的,去掉它。总之,一组向量总能生成一个线性空间,维数不大于向量个数
现在,给定一组多项式 $f_1, f_2, \dots, f_k$,它们生成一个理想(ideal) $I = \langle f_1, \dots, f_k \rangle$ ,你可以非常粗略地类比成线性空间。我们希望在这组多项式生成的理想中找到一些性质“好”的基,完成消元。
如果我们能在Gröbner基中找到一元多项式,那就成功完成了消元。如果这个多项式的性质比较好(比如,次数小于等于4),那就能得到方程组的解析解。
看懂求Gröbner基的代码的必要概念补充
注:对于多项式环,需要知道抽象代数里有这么个概念。而单项式和字典序非常容易理解。
- 单项式:常数和一些变量的乘积,比如 $4x2y3$ 。单项式求和就是多项式
- 环:在集合R中定义两种运算:加法和乘法,满足下面的性质,就说 $(R,+,)$ 构成环:1. $(R,+)$ 是交换群(加法封闭、结合律、单位元存在、每个元素有逆元、交换律)2. $(R,)$ 是半群(乘法封闭、结合律、单位元存在)3. 乘法对加法满足左右两边的分配律: $(a+b)c=ac+bc,\ c(a+b)=ca+cb$
- 多项式环:有环R, $R[x]={f(x)=\sum_{k=0}^{n} a_{k}x^k|a_{k} \in R}$ 是R上多项式集,称 $(R[x],+,*)$ 为多项式环。把 $R[x]$ 再次代入可以定义多元多项式环 $R[x,y]=R[x][y],\ R[x,y,z]=R[x,y][z],\ \cdots$ 。简单理解: $R[x][y]$ 表示以y为主元,系数是关于x的多项式(分别从主元视角和单项式视角理解多元多项式)
- 字典序:为了实现消元求出Gröbner基的过程,需要规定单项式之间的顺序关系,它会影响消元顺序。规定方式不唯一,我们仅介绍字典序。千言万语不如一个例子:设单项式 $kxaybz^c$ ,且 $x>y>z$ ,则可以写出4元组 $(a,b,c,k)$ 。对于两个4元组,优先比较a的大小,a大则4元组大,a一样则比较b,b也一样则比较c,以此类推。
最下面的代码块是非常好的例子。把玩一下就知道字典序的规则细节了,从左到右、从上到下,单项式就从大到小:
'''
3*t^2*x^2 -> (2, 2, 0) 2*t^2*x^2 -> (2, 2, 0) t^2*x^2 -> (2, 2, 0)
t^2*x*y^3 -> (2, 1, 3) t^2*x*y^2 -> (2, 1, 2) t*x^5*y^10 -> (1, 5, 10)
t*x^4*y^11 -> (1, 4, 11) x^3*y -> (0, 3, 1) x^2*y^99 -> (0, 2, 99)
x^2*y^2 -> (0, 2, 2) 114514*y^100 -> (0, 0, 100) y^100 -> (0, 0, 100)
1919810 -> (0, 0, 0)
'''
SageMath简介
SageMath:开源Python数学软件,在Python语法基础上增加了些语法糖
在线运行sage代码: https://sagecell.sagemath.org/ 。只需要复制下面的代码去这个网站运行,就能无痛体验SageMath:
x, y, t = var('x y t')
sols = solve([2 * t * x + y + 2, 2 * t * y + x + 1, x ^ 2 + y ^ 2 - 1])
print(sols) # 我们想要的: [y == 0.576378809869376, x == 0.8171826341820846, t == -1.576378721327477] ,排除一个y=0,以及两个复数根
运行环境:Windows10 WSL2 Ubuntu-24.04
运行命令:按官方文档提示,运行conda activate sage后,就能使用命令sage '1-(x+1)(y+2)-prob/solve_directly.sage'来运行sage代码了。
- 文件扩展名必须是
.sage。sage在Python的基础上添加了些语法糖 - 命令执行后,会生成一个
.py文件,比如上面的命令会生成1-(x+1)(y+2)-prob/solve_directly.sage.py
写sage代码破解钓鱼题!
铺垫了这么多,终于可以看代码了!很遗憾,万众瞩目的大语言模型没能力一次写出这里展示的代码,所以我的讲解暂时还是有价值的。
第一段代码
R.<t, x, y> = PolynomialRing(QQ, order='lex')
f = (x + 1) * (y + 2) + t * (x ^ 2 + y ^ 2 - 1)
fdx = diff(f, x)
fdy = diff(f, y)
fdt = diff(f, t)
print(fdx, fdy, fdt)
I = ideal(fdx, fdy, fdt).groebner_basis()
print(I)
运行结果:
'''
偏导: 2*t*x + y + 2 2*t*y + x + 1 x^2 + y^2 - 1
(和《拉格朗日乘数法-实操》展示的结果一样)。Gröbner基:
[t + 2*y^3 + 4*y^2 + 3/2*y - 1,
x - 2*y^2 - 2*y + 1,
y^4 + 2*y^3 + 1/4*y^2 - y]
'''
这段代码:
- 定义三元多项式环 R,变量是
t, x, y,系数在QQ(有理数域)中。order='lex'表示序关系规则采用字典序(lexicographic order,前面介绍的),且 $t>x>y$ - 定义拉格朗日函数,然后调用
diff()求偏导 ideal()构造由这三个偏导组成的多项式理想,.groebner_basis()计算该理想的Gröbner基- 采用其他排序规则会得到不同的Gröbner基。并不是所有Gröbner基都含有我们感兴趣的消元结果,感兴趣的可以自己试试
- 运行结果:Gröbner基里的第3个多项式只含
y,这表明我们成功用Gröbner基完成了消元。并且,第2个多项式告诉我们,x能用y表示出来
第二段代码
y_func_factor = I[2].factor()
print(y_func_factor) # y_func_factor 只是运行来看看结果
y = var('y')
sols = solve(y ^ 3 + 2 * y ^ 2 + 1 / 4 * y - 1)
print(sols)
运行结果:
# (1/4) * y * (4*y^3 + 8*y^2 + y - 4)
# 方程有3个根,太长了这里放不下。前两个是复数,第三个是我们想要的
# 像下面这么写,求单变量多项式的根,也是OK的
y_func_sym = y ^ 3 + 2 * y ^ 2 + 1 / 4 * y - 1
sols = y_func_sym.roots()
wanted_y = sols[2][0]
factor()对多项式进行因式分解,我们需要先运行一次,查看结果来确定要解的次数更低的一元多项式方程。然后再写出下面那3行代码解方程- 运行结果:前两个是复数根,第三个根是我们想要的实根
第三段代码
wanted_y = sols[2].rhs()
wanted_y_n = wanted_y.n()
x = 2 * y ^ 2 + 2 * y - 1
wanted_x_n = x.subs(y=wanted_y).n()
goal = (x + 1) * (y + 2)
ans = goal.subs(y=wanted_y)
ans_simplified = ans.simplify_full()
n_ans = ans.n()
latex(wanted_y)
这段代码就非常容易理解了。但答案太长了,放到下一个章节展示
- sage的
solve()返回的解的类型是sage.symbolic.expression.Expression。只有二元关系才能调用.lhs(), .rhs()。对于二元关系y == 1/6,调用.lhs()得'y',调用.rhs()得1/6 - 变量
x的表达式也是从上一页展示的Gröbner基拿到的 - 调用
.n()可以把解析解转为数值解 - 调用
.subs()可以对表达式求值 - 调用
.simplify_full()尝试化简表达式 latex(wanted_y)拿到一个表达式的latex字符串,比如 $\sqrt{3}$ (\sqrt{3})
顺便在这里吐槽下latex()踩坑:输出的字符串有可能在Obsidian合法,但在slidev中不合法。bug原因可能是括号没有完全匹配。我暂时没想到好的解决办法,只好直接问LLM帮我输出相关公式
答案
是的,答案很长,需要新开一个章节来展示~
$$
y = \frac{1}{6} , {\left(3 , \sqrt{183} + 62\right)}^{\frac{1}{3}} + \frac{13}{6 , {\left(3 , \sqrt{183} + 62\right)}^{\frac{1}{3}}} - \frac{2}{3}
$$
数值解:x = 0.8171826, y = 0.576379, ans = 4.681751。答案的解析解:
$$
\begin{aligned}
\frac{1}{108} &\left( \left( \left(3 \sqrt{183} + 62\right)^{\frac{1}{3}} + \frac{13}{\left(3 \sqrt{183} + 62\right)^{\frac{1}{3}}} - 4 \right)^{2} + 6 \left(3 \sqrt{183} + 62\right)^{\frac{1}{3}} + \frac{78}{\left(3 \sqrt{183} + 62\right)^{\frac{1}{3}}} - 24 \right) \
&\left( \left(3 \sqrt{183} + 62\right)^{\frac{1}{3}} + \frac{13}{\left(3 \sqrt{183} + 62\right)^{\frac{1}{3}}} + 8 \right)
\end{aligned}
$$
调用simplify_full()化简后的答案:
$$
\frac{ \left(5 \sqrt{183} + 216\right) \left(3 \sqrt{183} + 62\right)^{\frac{2}{3}} + 24 \left(3 \sqrt{183} + 62\right)^{\frac{4}{3}} + 313 \sqrt{183} + 5004 }{ 12 \left(3 \sqrt{183} + 62\right)^{\frac{4}{3}} }
$$
附录
完整代码:
R.<t, x, y> = PolynomialRing(QQ, order='lex')
f = (x + 1) * (y + 2) + t * (x ^ 2 + y ^ 2 - 1)
fdx = diff(f, x)
fdy = diff(f, y)
fdt = diff(f, t)
print(fdx, fdy, fdt)
I = ideal(fdx, fdy, fdt).groebner_basis()
print(I)
y_func_factor = I[2].factor()
print(y_func_factor)
y = var('y')
sols = solve(y ^ 3 + 2 * y ^ 2 + 1 / 4 * y - 1)
print(sols)
wanted_y = sols[2].rhs()
wanted_y_n = wanted_y.n()
x = 2 * y ^ 2 + 2 * y - 1
wanted_x_n = x.subs(y=wanted_y).n()
goal = (x + 1) * (y + 2)
ans = goal.subs(y=wanted_y)
ans_simplified = ans.simplify_full()
n_ans = ans.n()
探究字典序的排序规则:
R.<t, x, y> = PolynomialRing(QQ, order='lex')
mon_order = R.term_order()
print('单项式序类型:', mon_order)
print('变量优先级(从高到低):', R.variable_names(), '\n')
m1 = t ^ 2 * x * y ^ 3
m2 = t ^ 2 * x ^ 2
m3 = t * x ^ 5 * y ^ 10
m4 = x ^ 3 * y
m5 = y ^ 100
m6 = t ^ 2 * x * y ^ 2 # 与 m1 比,仅 y 指数不同
m7 = 3 * t ^ 2 * x ^ 2 # 与 m2 比,仅系数不同
m8 = x ^ 2 * y ^ 99
m9 = t * x ^ 4 * y ^ 11
m10 = x ^ 2 * y ^ 2
m11 = 1919810 * y ^ 0
m12 = 114514 * y ^ 100
m13 = 2 * t ^ 2 * x ^ 2
monomials = [
m1, m2, m3, m4, m5, m6, m7,
m8, m9, m10, m11, m12, m13
]
print('单项式及其指数元组 (t, x, y):')
for m in monomials:
exp_tuple = m.exponents()[0]
print(f'{m} -> {exp_tuple}')
print('\n按 lex 顺序从大到小排序:')
sorted_mons = sorted(monomials, reverse=True)
for m in sorted_mons:
exp_tuple = m.exponents()[0]
print(f'{m} -> {exp_tuple}')
'''
3*t^2*x^2 -> (2, 2, 0)
2*t^2*x^2 -> (2, 2, 0)
t^2*x^2 -> (2, 2, 0)
t^2*x*y^3 -> (2, 1, 3)
t^2*x*y^2 -> (2, 1, 2)
t*x^5*y^10 -> (1, 5, 10)
t*x^4*y^11 -> (1, 4, 11)
x^3*y -> (0, 3, 1)
x^2*y^99 -> (0, 2, 99)
x^2*y^2 -> (0, 2, 2)
114514*y^100 -> (0, 0, 100)
y^100 -> (0, 0, 100)
1919810 -> (0, 0, 0)
'''
本期视频的代码不难,为什么LLM竟没能力生成?
有些问题有多个方案:
- 一次性写出解决整个问题的代码
- 先写一部分代码,运行看看中间结果,再根据中间结果写下一部分代码
有时我们会碰上这种情况:理论上两个方案都能解决问题,但方案1的代码复杂度显著高于方案2,或者我们用的包缺乏支持方案1的API,导致LLM在生成方案1的代码时很容易产生各种各样的错误和幻觉。人类很容易想到,有时多拆解一步动作就能大幅简化需求,但对LLM来说意识到这件事就很难。
参考资料
SageMath官方文档,包含怎么安装、怎么写sage代码等内容: https://doc.sagemath.org/html/en/tutorial/index.html



 浙公网安备 33010602011771号
浙公网安备 33010602011771号