Segment Tree / Binary Indexed Tree

参见 307. Range Sum Query - Mutable

Segment Tree

Tree Implementation (SegmentTreeNode)

https://www.youtube.com/watch?v=rYBtViWXYeI&list=PLLuMmzMTgVK7ug02DDoQsf50OtwVDL1xd&index=1
https://leetcode.com/problems/range-sum-query-mutable/discuss/75711/C++-Segment-Treeupdate-and-sum-are-both-O(logn)

struct SegmentTreeNode {
    int start, end, sum;
    SegmentTreeNode* left;
    SegmentTreeNode* right;
    SegmentTreeNode(int a, int b):start(a),end(b),sum(0),left(NULL),right(NULL){}
};

class NumArray {
private:
    SegmentTreeNode* root;
    
    // build tree from array[start~end]
    SegmentTreeNode* buildTree(vector<int> &nums, int start, int end){
        if (start>end) return NULL; //error
        SegmentTreeNode *root=new SegmentTreeNode(start,end);
        if (start==end) {
            root->sum = nums[start];
            return root;
        }
        int mid = (start+end)/2;
        root->left = buildTree(nums,start,mid);
        root->right = buildTree(nums,mid+1,end);
        root->sum = root->left->sum + root->right->sum;
        return root;
    }

    void updateTree(SegmentTreeNode *root, int i, int val){
        if (root->start==i && root->end==i){
            root->sum = val;
            return;
        }
        int mid = (root->start+root->end)/2;
        if (i<=mid){
            updateTree(root->left,i,val);
        }else{
            updateTree(root->right,i,val);
        }
        root->sum = root->left->sum + root->right->sum;
    }

    int queryTree(SegmentTreeNode *root, int i, int j){
        if (root->start==i && root->end==j)
            return root->sum;
        int mid = (root->start+root->end)/2;
        // [start~mid] [mid+1~end]
        if (j<=mid){
            return queryTree(root->left,i,j);
        }else if (i>mid){
            return queryTree(root->right,i,j);
        }else{
            return queryTree(root->left,i,mid) + queryTree(root->right,mid+1,j);
        }
    }
    
public:
    NumArray(vector<int> &nums) {
        int n = nums.size();
        root = buildTree(nums,0,n-1);
    }
   
    void update(int i, int val) {
        updateTree(root,i,val);
    }

    int sumRange(int i, int j) {
        return queryTree(root,i,j);
    }
};

/**
 * Your NumArray object will be instantiated and called as such:
 * NumArray* obj = new NumArray(nums);
 * obj->update(i,val);
 * int param_2 = obj->sumRange(i,j);
 */

时间复杂度 O(logn)，可能会更多一点，和遍历到的node个数也有关。

 

Array Implementation

Since a Segment Tree is a binary tree, a simple linear array can be used to represent the Segment Tree.
https://leetcode.com/articles/a-recursive-approach-to-segment-trees-range-sum-queries-lazy-propagation/
https://www.hackerearth.com/zh/practice/data-structures/advanced-data-structures/segment-trees/tutorial/

 

 

Binary Indexed Tree

Binary Indexed Tree 本质是求解数组前i个元素的数据结构。BIT 相比 Segment Tree 实现起来更容易，但比较tricky。

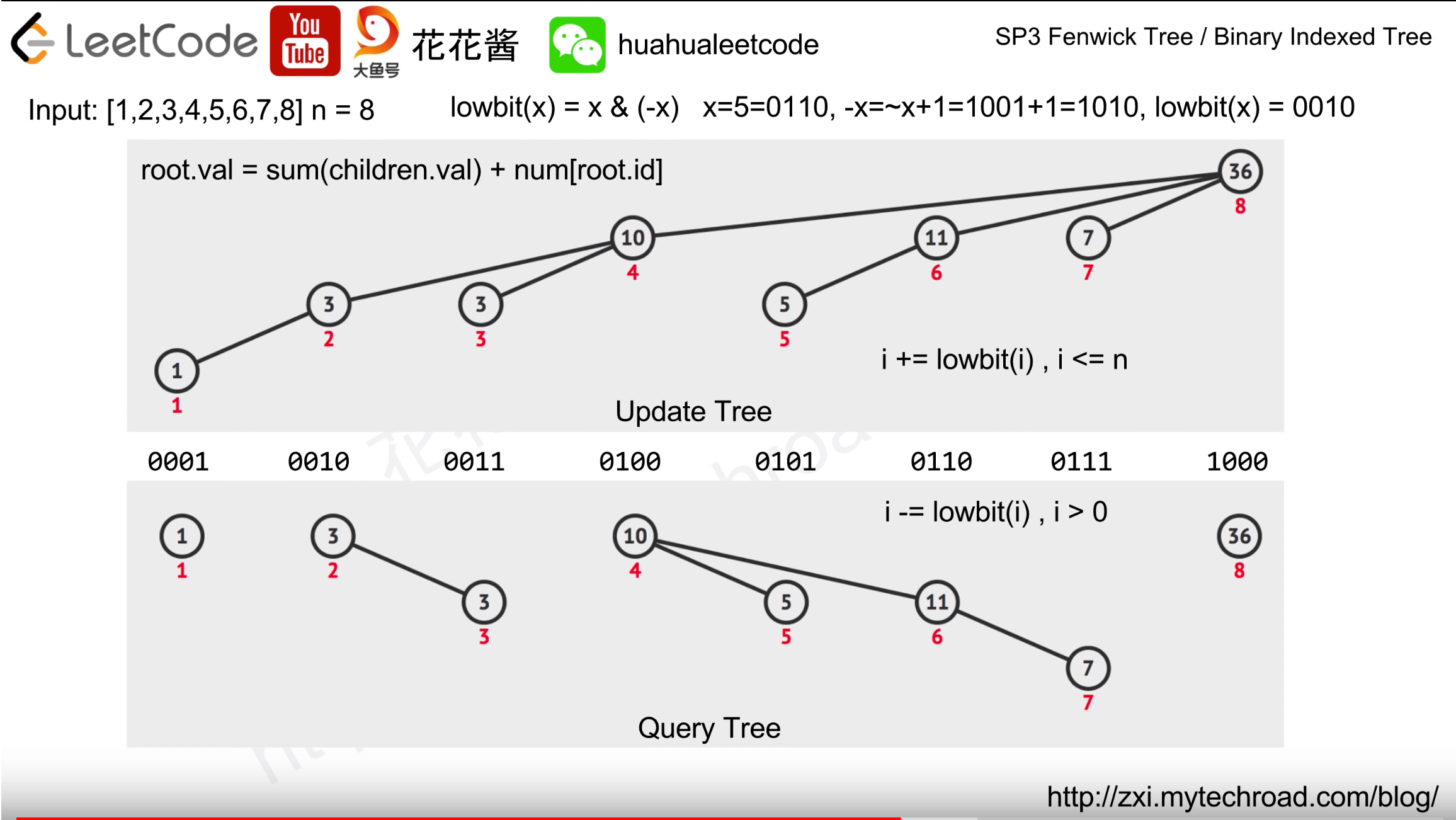
* 对于一个二进制数，我们可以通过 x & (-x) 得到最低位的1 (-x=~x+1，即2's complement，补码)。

BIT 的核心一个是update，一个是query，两者略有不同。

update时，不断加上最低位的1得到新节点，并同时更新该节点；

query时，不断减去最低位的1得到新节点，所有这些节点的和为query的值。

https://www.youtube.com/watch?v=CWDQJGaN1gY
https://www.geeksforgeeks.org/binary-indexed-tree-or-fenwick-tree-2/
https://www.youtube.com/watch?v=WbafSgetDDk&list=PLLuMmzMTgVK5Hy1qcWYZcd7wVQQ1v0AjX&index=15&t=0s

 

class NumArray {
private:
    vector<int> BIT;
    vector<int> nums;
    
    // increase nums[i] by val
    void updateBIT(int index, int val){
        // index in BIT is 1 more than the index in array
        index += 1; 
        while (index<BIT.size()){
            BIT[index] += val;
            index += (index & -index);
        }
    }
    
    // sum of nums[0~index]
    int getSum(int index){
        index += 1;
        int sum=0;
        while (index>0){
            sum += BIT[index];
            index -= (index & -index);
        }
        return sum;
    }
    
public:
    NumArray(vector<int>& nums) {
        BIT.resize(nums.size()+1, 0);
        this->nums = nums;
        for (int i=0;i<nums.size();++i)
            updateBIT(i,nums[i]);
    }
    
    void update(int i, int val) {
        updateBIT(i, val-nums[i]);
        nums[i] = val;
    }
    
    int sumRange(int i, int j) {
        return getSum(j) - getSum(i-1);
    }
};

/**
 * Your NumArray object will be instantiated and called as such:
 * NumArray* obj = new NumArray(nums);
 * obj->update(i,val);
 * int param_2 = obj->sumRange(i,j);
 */

 

别人的总结：

https://yijiajin.github.io/leetcode/2016/12/22/Leetcode-Segment-Tree-Binary-Index-Tree/