点位精度评定
目录
第1章点位精度评定
1.1 简介
下图显示了一系列的散点。点位精度评定就是计算一些数值,用来评定这些点的离散程度。精度评定数值越小说明点的离散程度越小,精度越高。
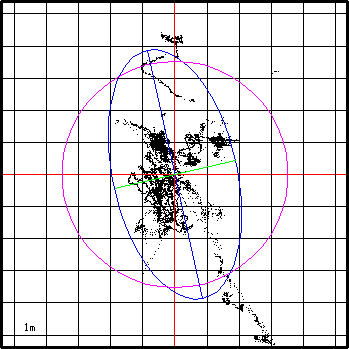
1.2 期望
上图的圆心和椭圆中心,是散点的真实位置。假定其坐标为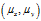 ,那么
,那么 就是随机变量
就是随机变量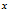 的期望,
的期望, 就是随机变量
就是随机变量 的期望。
的期望。
期望的数值,有可能是已知的,也可能是未知的。在未知的情况下,需要对期望进行估值。一般情况下,期望的估值采用的是算术平均值,即:
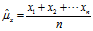
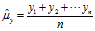
1.3 方差
方差用来描述随机变量的离散程度,它的数值越小说明离散度越低。
随机变量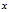 的方差:
的方差: 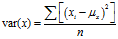
随机变量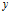 的方差:
的方差: 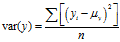
注意:如果随机变量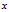 的期望
的期望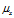 使用的是估计值
使用的是估计值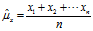 ,则方差的估值为
,则方差的估值为 。把
。把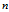 改成
改成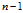 的原因在于:求出
的原因在于:求出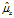 后,
后, 的自由度由
的自由度由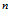 变成了
变成了 。
。
1.4 标准差
标准差也叫中误差,它是方差的平方根,即:
随机变量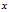 的标准差:
的标准差:  或
或 
随机变量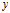 的标准差:
的标准差: 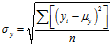 或
或 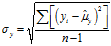
1.5 协方差
随机变量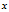 、
、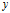 之间的协方差:
之间的协方差:
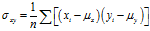
同样的,如果期望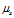 和
和 使用的是估计值,则
使用的是估计值,则 按下式计算
按下式计算
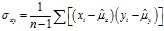
1.6 DRMS
离散随机变量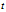 的均方根RMS(Root Mean Square)为:
的均方根RMS(Root Mean Square)为:

点位误差里的RMS其实是距离均方根差(DRMS),即:

将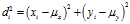 代入上式,可得
代入上式,可得
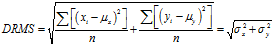
1.7 2DRMS
双倍距离均方根 的计算公式如下:
的计算公式如下:

1.8 CEP
圆概率误差CEP(Circular Error Probable)的含义:以 为圆心,CEP为半径画一个圆,点落入圆内的概率为50%。其计算公式如下:
为圆心,CEP为半径画一个圆,点落入圆内的概率为50%。其计算公式如下:
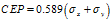
1.9 CEP95
CEP95(也被称之为R95)的含义:以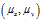 为圆心,CEP95为半径画一个圆,点落入圆内的概率为95%。其计算公式如下:
为圆心,CEP95为半径画一个圆,点落入圆内的概率为95%。其计算公式如下:
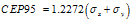
1.10 CEP99
CEP99的含义:以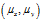 为圆心,CEP99为半径画一个圆,点落入圆内的概率为99%。其计算公式如下:
为圆心,CEP99为半径画一个圆,点落入圆内的概率为99%。其计算公式如下:
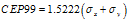
1.11 对比
CEP、CEP95、CEP99之间是有严格的比例关系的;DRMS、2DRMS之间也是有严格的比例关系的;那么CEP与DRMS有什么关系呢?
假定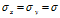 ,则:
,则: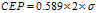 ,
,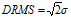 。此时
。此时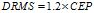 。
。
换句话说就是CEP与DRMS之间有着近似的转换公式: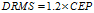
这几个统计量从小到大依次为:CEP、DRMS、CEP95、2DRMS、CEP99。
以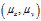 为圆心,各个统计量为半径,点落入这个圆的概率见下表:
为圆心,各个统计量为半径,点落入这个圆的概率见下表:
|
统计量 |
概率 |
|
CEP |
50% |
|
DRMS |
63%~68% |
|
CEP95 |
95% |
|
2DRMS |
95%~98% |
|
CEP99 |
99% |
1.12 SEP
SEP的含义:以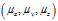 为球心,SEP为半径画一个圆球,点落入球内的概率为50%。其计算公式如下:
为球心,SEP为半径画一个圆球,点落入球内的概率为50%。其计算公式如下:

1.13 误差椭圆
在二维平面内,点位沿着任意方向 的方差按下式计算:
的方差按下式计算:
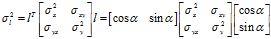
化简后可得:
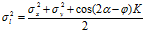
上式中
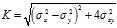
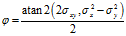
注意: 表示原点到
表示原点到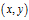 的方位角。
的方位角。
当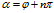 时(
时( )
)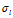 取最大值
取最大值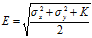 ;
;
当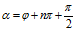 时(
时(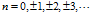 )
)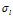 取最小值
取最小值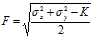 。
。
这里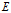 就是误差椭圆的长半轴,
就是误差椭圆的长半轴,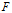 就是误差椭圆的短半轴,
就是误差椭圆的短半轴, 是长半轴的方位角。
是长半轴的方位角。
1.14 置信椭圆
长半轴为 、短半轴为
、短半轴为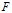 的椭圆被称之为标准误差椭圆。置信椭圆是标准误差椭圆的
的椭圆被称之为标准误差椭圆。置信椭圆是标准误差椭圆的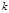 倍。
倍。
点落入置信椭圆内的概率为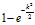
将 代入上式可求出点落入标准误差椭圆内的概率为39.35%。也就是说置信度39.35%的置信椭圆就是标准误差椭圆。
代入上式可求出点落入标准误差椭圆内的概率为39.35%。也就是说置信度39.35%的置信椭圆就是标准误差椭圆。
1.15 误差椭球
在三维空间,点位沿着任意方向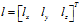 的方差按下式计算:
的方差按下式计算:
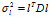
上式中的 是随机变量
是随机变量 的方差、协方差矩阵。
的方差、协方差矩阵。
注意方向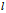 是单位向量,即满足
是单位向量,即满足
现在的问题是: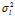 何时最大?何时最小?它的实质就是在满足
何时最大?何时最小?它的实质就是在满足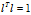 的条件下,求出
的条件下,求出 的极值。
的极值。
可根据拉格朗日乘数法求极值,其步骤为:
构造拉格朗日函数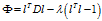 ,然后求解如下方程组:
,然后求解如下方程组:
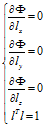
记 (即一个数对一个列向量求导),则
(即一个数对一个列向量求导),则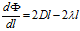 。根据上式可知
。根据上式可知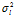 取极值时
取极值时 。
。
满足 的
的 是矩阵
是矩阵 的特征值,而
的特征值,而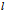 是与
是与 对应的特征向量。
对应的特征向量。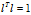 表示需要将特征向量单位化。
表示需要将特征向量单位化。
求出矩阵 的特征值和特征向量后,矩阵
的特征值和特征向量后,矩阵 可被对角化,即:
可被对角化,即:

上式中 是由特征值组成的对角阵,即
是由特征值组成的对角阵,即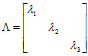 。
。
矩阵 的第
的第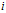 列是
列是 对应的单位特征向量。此时:
对应的单位特征向量。此时:
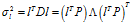
记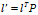 ,它的几何意义为:对向量
,它的几何意义为:对向量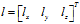 做正交变换,得到向量
做正交变换,得到向量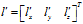 ,此时:
,此时:
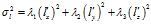
这里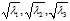 就是误差椭球的三个半轴,从大到小依次为长半轴、中半轴、短半轴。这三个半轴的方向就是特征向量的方向,它们是相互垂直的。
就是误差椭球的三个半轴,从大到小依次为长半轴、中半轴、短半轴。这三个半轴的方向就是特征向量的方向,它们是相互垂直的。
以椭球的三个半轴分别为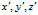 轴建立一个新的三维直角坐标系
轴建立一个新的三维直角坐标系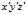 ,坐标系
,坐标系 到
到 的正交变换矩阵就是
的正交变换矩阵就是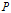 。
。
1.16 求解误差椭球
本节将求解矩阵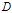 的特征值、特征向量
的特征值、特征向量
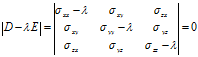
注意上式中: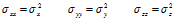
展开后可以得到一个一元三次方程: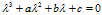 ,其中
,其中

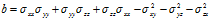
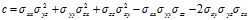
可以去除这个一元三次方程的二次项,如下式所示:
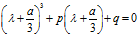
其中
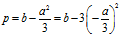
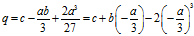
一元三次方程的三个根为:
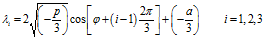
上式中
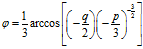
这三个根就是矩阵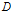 的特征值。因为
的特征值。因为 是正定的,所以这三个特征值必定都是大于零的实数。
是正定的,所以这三个特征值必定都是大于零的实数。
下面是矩阵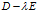 的伴随矩阵:
的伴随矩阵:
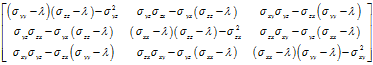
将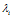 代入上式,每一列就是
代入上式,每一列就是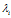 对应的一个特征向量,请选用长度最大的特征向量并将其单位化。
对应的一个特征向量,请选用长度最大的特征向量并将其单位化。
注意:按上述方法求出的特征向量有可能为零,此时至少有两个特征值是相等的。换句话说就是上述求解特征向量的算法要求三个特征值均不相等。
1.17 置信椭球
三个半轴为 的椭球是标准误差椭球,置信椭圆是标准误差椭圆的
的椭球是标准误差椭球,置信椭圆是标准误差椭圆的 倍。
倍。
点落入置信椭球内的概率为
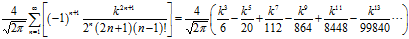
将 代入上式可求出点落入标准误差椭球内的概率为19.87%。也就是说置信度19.87%的置信椭球就是标准误差椭球。
代入上式可求出点落入标准误差椭球内的概率为19.87%。也就是说置信度19.87%的置信椭球就是标准误差椭球。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号