牛顿迭代法（大白话）

解释：

首先看图：曲线与X轴（横坐标）的切点就是曲线的根

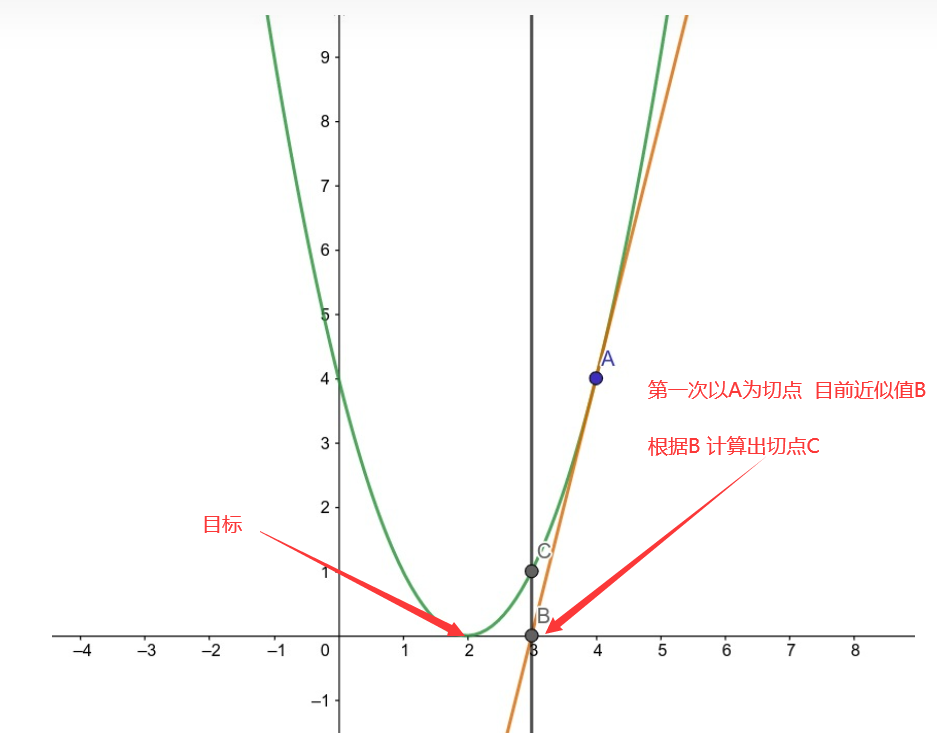
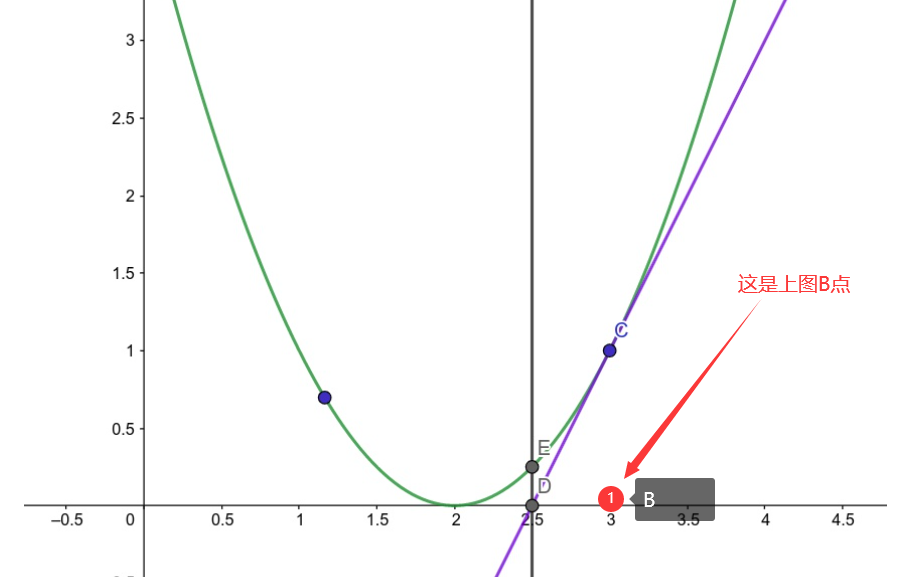
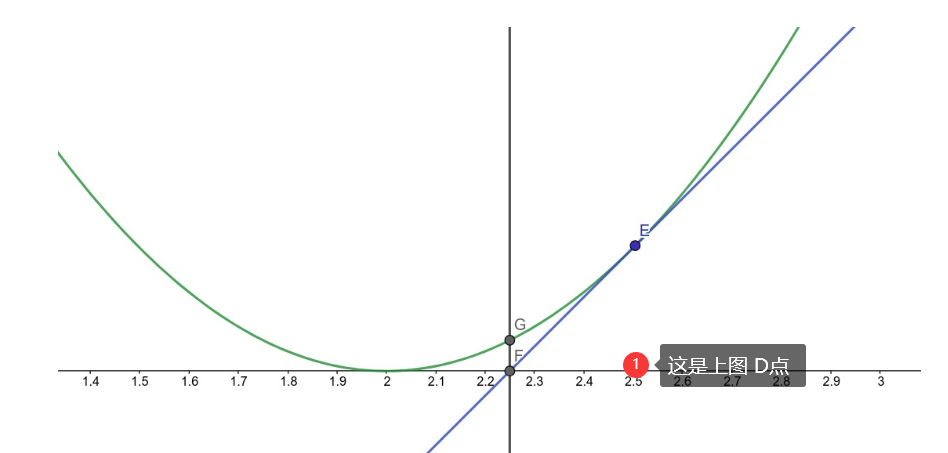
经过无数次取切线，就会发现，慢慢靠近曲线的根。

这就是牛顿迭代法，大致思路理解了吧。

公式

\[\chi_{n+1}=\chi_{n}-\frac {f(\chi_{n})}{f\prime{}(\chi_{n})} \]

那么根据该公式可以按以下步骤求解一元方程的任意次的根
(1) 选一个方程的近似根，赋给变量X0，x1是根据牛顿迭代公式计算
(2) 将x1的值保存于变量x0，然后牛顿迭代公式计算并将结果存于变量x1;
(3) 当x0与x1的差的绝对值还小于指定的精度要求时，重复步骤(2)的计算。

若方程有根，并且用上述方法计算出来的近似根序列收敛，则按上述方法求得的x0就认为是方程的根。

Java代码

public class Main {
	//表示原式子 F(x)
	static double f(double x){
		return 2*x*x*x-4*x*x+3*x-6;
	}
	//表示导函数 f(x）
	static double fd(double x){
		return 6*x*x-8*x+3;
	}
	public static void main(String[] args){
		double x0=1.5;
		double x1=1.5;
		//套入公式
		do{
			x0=x1;
			x1=x0-f(x0)/fd(x0);
		}
		while(Math.abs(x1-x0)>=1e-5);
		//输出结果
		System.out.println(x1);
	}
}

python代码

# 表示原函数 F(x)
def f(x):
	return 2*x*x*x-4*x*x+3*x-6
# 表示导函数 f(x)
def fd(x):
	return 6*x*x-8*x+3


def cal():
        # 可以取任意值，只是循环次数不同而已
	x0=100
	x1=x0-f(x0)/fd(x0)
	
	while abs(x1-x0)>=1e-5:
		x0=x1
		x1=x0-f(x0)/fd(x0)
	return x1
print(cal())

leetcode练习题

https://leetcode.cn/problems/sqrtx/