信息熵

信息熵的公式：

 

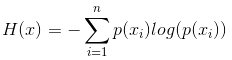
信息量：

信息量是对信息的度量，也相当于理论上所需的存储空间。信息量的大小与事件发生的概率成反比，因为越大概率的事件使人产生的印象越小，从而信息量也就越小。

令事件x的信息量为h(x)，x、y为两个不相关事件，显然满足以下性质：
h(x,y) = h(x) + h(y)
又有 p(x,y) = p(x) * p(y)
可以推出 h(x) = -log p(x)

 

信息熵：

信息熵是可能产生的信息量的期望（系统复杂程度的度量）。

import numpy as np
def entropy(a):
    h = 0
    for b in a:
        p = b / sum(a)
        h -= p * np.log(p)
    return h / np.log(2)

例：
entropy(抛硬币) = entropy(["正","反"]) = entropy([1,1]) = 1.0
entropy(英文) = entropy(["a",...,"z"]) = entropy([1,...,1]) = 4.700439718141094
entropy(彩票) = entropy(["未中奖",...,"未中奖","中奖"]) = entropy([1,100000000]) = 2.801811953267915e-07