Treap

Treap = Tree + Heap

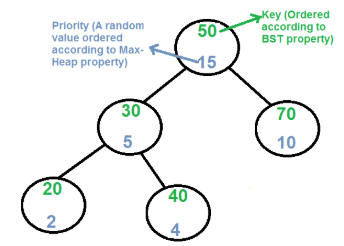
Treap的每个节点保存两个值

（1）键值（维持BST的熟悉）

（2）优先级（随机生成，维持Heap的属性）

 

 支持六个操作：

（1）插入节点

（2）删除节点

（3）查询数x的排名

（4）查询排名为x的数

（5）查询数x的前驱（求树中比x小的最大数）

（6）查询数x的后继（求树中比x大的最小数）

时间复杂度均为O(logn)

各数组的含义：

sz[i] （以i为根的子树的结点数）

v[i]（结点i的权值）

rd[i[（结点i的优先级）

num[i]（可能有重复，所以表示结点i存储的数的个数）

ch[i][2]（结点i的左右儿子）

 

因为结点经常换位置，所以需要经常修正sz数组：

void pushup(int p) {
    sz[p] = sz[son[p][0]] + sz[son[p][1]] + num[p];
}

结点的左右旋转：

void rotate(int &p, int d) {
    int k = son[p][d ^ 1];
    son[p][d ^ 1] = son[k][d];
    son[k][d] = p;
    pushup(p);
    pushup(k);
    p = k;
}

（1）插入：

void ins(int &p, int x) {
    if(!p) {
        p = ++sum;
        sz[p] = num[p] = 1;
        v[p] = x;
        rd[p] = rand();
        return;
    }
    if(v[p] == x) {
        num[p]++;
        sz[p]++;
        return;
    }
    int d = (x > v[p]);
    ins(son[p][d], x);
    if(rd[p] < rd[son[p][d]]) rotate(p, d ^ 1);
    pushup(p);
}

（2）删除：

void del(int &p, int x) {
    if(!p) return;
    if(x < v[p]) del(ch[p][0], x);
    else if(x > v[p]) del(ch[p][1], x);
    else {
        if(!ch[p][0] && !ch[p][1]) {
            sz[p]--;
            num[p]--;
            if(!sz[p]) p = 0;
        }
        else {
            int d = (rd[ch[p][0]] > rd[ch[p][1]]);
            rotate(p, d);
            del(ch[p][d], x);
        }
    }
    pushup(p);
}

（3）查询数x的排名：

int rk(int p, int x) {
    if(!p) return 0;
    if(v[p] == x) return sz[ch[p][0]] + 1;
    if(v[p] < x) return sz[ch[p][0]] + num[p] + rk(ch[p][1], x);
    if(v[p] > x) return rk(ch[p][0], x);
}

（4）查询排名为x的数：

int fd(int p, int x) {
    if(!p) return 0;
    int c = sz[ch[p][0]];
    if(x <= c) return fd(ch[p][0], x);
    else if(x > c + num[p]) return fd(ch[p][1], x - c - num[p]);
    else return v[p];
}

（5）查询数x的前驱：

int pre(int p, int x) {
    if(!p) return -inf;
    if(v[p] >= x) return pre(ch[p][0], x);
    else  return max(v[p], pre(ch[p][1], x));
}

（6）查询数x的后继：

int post(int p, int x) {
    if(!p) return inf;
    if(v[p] <= x) return post(ch[p][1], x);
    else return min(v[p], post(ch[p][0], x));
}

 

模板题：洛谷P3369

#include<bits/stdc++.h>
using namespace std;

const int maxn = 1e5 + 5;
const int inf = 2e9 + 5;

int sum = 0;
int sz[maxn], v[maxn], num[maxn], rd[maxn], ch[maxn][2];

void pushup(int p) {
    sz[p] = sz[ch[p][0]] + sz[ch[p][1]] + num[p];
}

void rotate(int &p, int d) {
    int k = ch[p][d ^ 1];
    ch[p][d ^ 1] = ch[k][d];
    ch[k][d] = p;
    pushup(p);
    pushup(k);
    p = k;
}

void ins(int &p, int x) {
    if(!p) {
        p = ++sum;
        sz[p] = num[p] = 1;
        v[p] = x;
        rd[p] = rand() + 1;
        return;
    }
    if(v[p] == x) {
        num[p]++;
        sz[p]++;
        return;
    }
    int d = (x > v[p]);
    ins(ch[p][d], x);
    if(rd[p] < rd[ch[p][d]]) rotate(p, d ^ 1);
    pushup(p);
}

void del(int &p, int x) {
    if(!p) return;
    if(x < v[p]) del(ch[p][0], x);
    else if(x > v[p]) del(ch[p][1], x);
    else {
        if(!ch[p][0] && !ch[p][1]) {
            sz[p]--;
            num[p]--;
            if(!sz[p]) p = 0;
        }
        else {
            int d = (rd[ch[p][0]] > rd[ch[p][1]]);
            rotate(p, d);
            del(ch[p][d], x);
        }
    }
    pushup(p);
}

int rk(int p, int x) {
    if(!p) return 0;
    if(v[p] == x) return sz[ch[p][0]] + 1;
    if(v[p] < x) return sz[ch[p][0]] + num[p] + rk(ch[p][1], x);
    if(v[p] > x) return rk(ch[p][0], x);
}

int fd(int p, int x) {
    if(!p) return 0;
    int c = sz[ch[p][0]];
    if(x <= c) return fd(ch[p][0], x);
    else if(x > c + num[p]) return fd(ch[p][1], x - c - num[p]);
    else return v[p];
}

int pre(int p, int x) {
    if(!p) return -inf;
    if(v[p] >= x) return pre(ch[p][0], x);
    else  return max(v[p], pre(ch[p][1], x));
}

int post(int p, int x) {
    if(!p) return inf;
    if(v[p] <= x) return post(ch[p][1], x);
    else return min(v[p], post(ch[p][0], x));
}

int T, a, b, rt = 0;
int main() {
    cin >> T;
    while(T--) {
        cin >> a >> b;
        if(a == 1) ins(rt, b);
        else if(a == 2) del(rt, b);
        else if(a == 3) cout << rk(rt, b) << endl;
        else if(a == 4) cout << fd(rt, b) << endl;
        else if(a == 5) cout << pre(rt, b) << endl;
        else cout << post(rt, b) << endl;
    }
}