WebGL学习笔记(五):变换库
2019-08-01 15:32 阿诚de窝 阅读(1521) 评论(0) 收藏 举报在WebGL开始绘制之前,我们需要通过自己对3D空间进行矩阵和向量的运算,使用网上已经成熟的转换库,可以避免自己去实现这些复杂的数学运算。
我们这里选择的是gl-matrix库,下载地址:https://github.com/toji/gl-matrix
变换运算
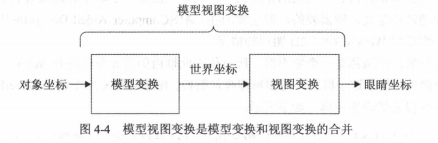
在最终开始绘制之前,我们需要把3D世界中的物体的坐标系转换为WebGL的坐标系,确定最终绘制的位置。
模型变换(顶点着色器阶段处理)
模型变换用来确定一个模型在世界坐标系中的位置,所有的模型都有一个世界坐标系的矩阵,保证所有模型都处于同一个坐标系(即世界坐标系)之中,模型变换包括平移,旋转和缩放;
视图变换(顶点着色器阶段处理)
有了世界坐标系之后还不够,还需要一个同样位于该坐标系之中的摄像机的矩阵,用来表示观察者观看的位置和角度;
模型视图变换(顶点着色器阶段处理)
该变换就是模型变换和视图变换相乘之后的变换矩阵;
投影变换(顶点着色器阶段处理)
我们在这一步得到了物体在摄像机中看起来的最终坐标,但是和我们人眼可以看见的景象还是有所区别,比如我们看世界上的东西都是由一种近大远小的透视效果,投影变换就是用来实现这些效果的变换;
正交投影
正交投影,可以看做是一种平行投影,正交投影下的物体没有近大远小的视觉效果,无论远近看起来都是一样大的,该投影一般用在2D或2.5D(一般是3D角色2D场景)游戏中,3D游戏的UI实现也会用到该投影;
使用gl-matrix库创建正交投影代码如下:
1 var m4 = glMatrix.mat4.create(); 2 // 通过设定每个面的大小确定投影区域 3 glMatrix.mat4.ortho(m4, -100, 100, -100, 100, -100, 100);
透视投影
透视投影,可以模拟人眼所看见的3D世界的近大远小的视觉效果,该投影一般用在3D游戏中;
使用gl-matrix库创建透视投影代码如下:
1 var m4 = glMatrix.mat4.create(); 2 // 方法1:通过垂直范围、高宽比和近远面确定投影区域 3 glMatrix.mat4.perspective(m4, 1, 1, 0, 100); 4 // 方法2:通过设定每个面的大小确定投影区域 5 glMatrix.mat4.frustum(m4, -100, 100, -100, 100, -100, 100);
透视除法(图元装配阶段处理)
透视除法即使用w分量除以x,y,z分量(w默认值是1),产生三维的透视效果。
更多的信息可以参考:https://www.jianshu.com/p/7e701d7bfd79
视口变换(图元装配阶段处理)
视口变换主是将三维空间中的物体投影到二维的平面上,在计算机图形学中,它的定义是将经过几何变换,投影变换和裁剪变换后的物体显示于屏幕指定区域内。
用户可以通过调用两个方法来控制这个步骤的变换:
gl.viewPort
确定最终显示的位置和尺寸,单位为像素;
gl.depthRange
确定最终可以显示出来的深度区域,可选范围[0-1];
完整的变换管线(变换流水线)如下图所示

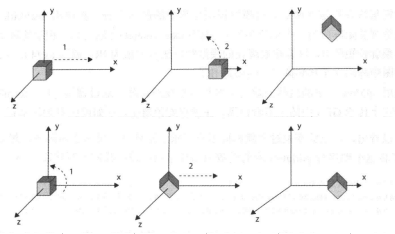
变换顺序的重要性
3D应用中矩阵的乘法非常重要,我们需要注意的是,矩阵的两个乘数交换之后,得到的结果是不一样的。
MN≠NM
可以看下面的图直观的了解下不同的变换顺序得到不同的结果:
变换矩阵堆栈
一般说来,矩阵堆栈常用于构造具有继承性的模型,即由一些简单目标构成的复杂模型。例如,一辆自行车就是由两个轮子、一个三角架及其它一些零部件构成的。它的继承性表现在当自行车往前走时,首先是前轮旋转,接着是后轮旋转,然后整个车身向前平移,如此进行下去,这样自行车就往前走了。
另外当我们需要实现复杂模型绘制时,会需要全局坐标和本地坐标的概念,比如,一个桌子放在全局坐标的某个位置上,这个桌子内部包含了一个桌面和四个腿,这5个模型的矩阵的数据是相对桌子的本地坐标,而不是记录全局坐标,我们希望,在桌子的矩阵改变时,内部的5个模型的本地矩阵不需要改变。
入栈
当前矩阵乘于栈顶矩阵之后的值,作为新的栈顶矩阵压入栈中,可以理解为当前栈顶矩阵就是的本地坐标使用的矩阵;
出栈
弹出栈顶的矩阵,当前的栈顶矩阵就是上一个本地坐标的父级坐标矩阵;
通过变换矩阵堆栈绘制桌子:
- 压入桌子的矩阵;
- 用栈顶矩阵乘于桌面的矩阵,得到桌面位于全局坐标的矩阵;
- 压入桌面的矩阵,当桌面上需要绘制物体时,可以使用该栈顶矩阵乘于需要绘制的物体的矩阵;
- 桌面已经没有物体需要绘制了,弹出栈顶的矩阵(即桌面的矩阵);
- 此时栈顶的矩阵即桌子的矩阵,用栈顶的矩阵乘于第一个腿的矩阵,得到第一个腿的全局坐标的矩阵;
如此往复,直到绘制完所有的模型;
示例
天道酬勤,功不唐捐!

 浙公网安备 33010602011771号
浙公网安备 33010602011771号