核心思想:
用参数方程表示一条直线
已知一条线段的起点(x1,y1)、终点(x2,y2),就可以通过一个参数u,表示这条线段所在直线上的任意一个点(x,y)
x=x1+u(x2-x1)
y=y1+u(y2-y1)
其中:
(x,y)是直线上任意一点
(x1,y1)是线段的起点
(x2,y2)是线段的终点
Δx是x2-x1
Δy是y2-y1
辅助概念
左下:入边
右上:出边
现在,
用u1表示可见部分的起点的参数u
用u2表示可见部分的终点的参数u
那么,
u1=max(0,ul,ub)
u2=min(1,ut,ur)
其中,
ul ub 分别是直线与窗口左边、下边交点的参数u
ut ur 分别是直线与窗口上边、右边交点的参数u
现在我们要的点(x,y)需要在窗口内,那么这个点的参数方程就要满足下面的不等式关系
我们关注的是参数u的值,要获取点(x,y),就要知道u值
为了方便,我们把不等式变成下面这个形式
再为了方便,用两个字母及其对应下标(8个变量)进行表记
这就有了
现在我们就得到了u的表达式
uk是窗口边界及其延长线的交点的对应参数值,将这个参数值代入方程就可以获取该点的位置
规律:
算法举例:
算法的具体步骤:
(1)输入线段的起点、终点(x1,y1 )、(x2,y2)以及窗口边界的横纵坐标:wxl、wxr、wyb和wyt。w代表窗口,windows。l、r、b、t分别代表left、right、bottom、top。
(2)直线水平的情况:
若△X=0,则p1=p2=0,此时进一步判断是否满足q1<0或q2<0 ,若满足,则该直线段不在窗口内,算法转(7)-结束。否则 ,满足q1≥0且q2≥0,则进一步计算umax和umin :
算法转(5)
(3)直线垂直的情况;
若△y=0,则p3=p4=0,此时进一步判断是否满足q3<0或q4<0 ,若满足,则该直线段不在窗口内,算法转(7)。否则,满 足q3 ≥0且q4 ≥0,则进一步计算umax和umin :
(4)一般情况:
若上述两条均不满足,则有pk≠0(k=1,2,3,4), 此时计算umax和umin:
(5)求得umax和umin后,进行判断:若umax>umin ,则直线段在窗口外,算法转(7)。若umax ≤umin,利用直线的参数方程
(6)利用直线的扫描转换算法绘制在窗口内的直线段
(7)算法结束









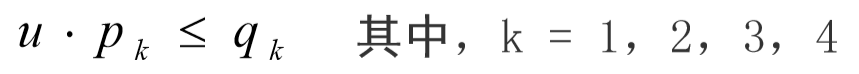
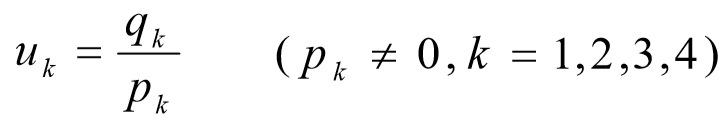






 算法转(5)
算法转(5)

 浙公网安备 33010602011771号
浙公网安备 33010602011771号