Python 学习记录（5）

Scikit-Learn 数据

简单介绍：

1. Scikit-Learn 除了完成监督学习和无监督学习之外，还提供了丰富地样本数据集、样本数据生成函数与数据处理方法。
2. 实现机器学习算法地训练、评估与预测。
3. 包含有样本数据集、生成样本数据、特征工程以及数据分割。

处理离群值

简单介绍

1. 离群值也叫逸出值，是指数据集中与其他数据点有明显差异的数据点，也就是说明显地偏大或者偏小。
2. 离群值会对数据分析和建模造成问题，因此需要对数据集中的离群值进行检测与处理。
3. 常用的检测方法包括基于统计学的方法、基于距离的方法、基于密度的方法以及基于模型的方法。

import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_blobs,make_moons
from sklearn.svm import OneClassSVM
from sklearn.covariance import EllipticEnvelope
from sklearn.ensemble import IsolationForest

#生成数据
n_samples = 500
outliers_fraction = 0.10
n_outliers=int(outliers_fraction*n_samples)
n_inliers = n_samples-n_outliers
X_outliers = np.random.uniform(low=-6,high=6,
                                size=(n_outliers,2))
np.random.RandomState(0)
blobs_params= dict(random_state=0,#这里先将参数定好。
                   n_samples=n_inliers,n_features=2)
datasets=[
    #centers表明中心点在哪里，cluster_std设置集群标准差
    make_blobs(centers=[[0,0],[0,0]],
               cluster_std=0.5,**blobs_params)[0],
    make_blobs(centers=[[2,2],[-2,-2]],
               cluster_std=[0.5,0.5],**blobs_params)[0],
    make_blobs(centers=[[2,2],[-2,-2]],
               cluster_std=[1.5,0.3],**blobs_params)[0],
    4.0*(make_moons(n_samples=n_samples,noise=0.05,
                    random_state=0)[0]-np.array([0.5,0.25]))]
    #使用make_moons函数生成一个月牙状的簇

#处理离群值
anomaly_algorithms=[
    EllipticEnvelope(contamination=outliers_fraction,
                     random_state=42),#创建椭圆包络的异常值检测模型。
    OneClassSVM(nu=outliers_fraction,kernel="rbf",
                gamma=0.1),#创建基于支持向量机的异常检测模型
    IsolationForest(contamination=outliers_fraction,
                    random_state=42)]#创建基于隔离森林的异常检测模型
#网格化数据，用来绘制等高线。
xx,yy=np.meshgrid(np.linspace(-7,7,150),
                  np.linspace(-7,7,150))
xy=np.c_[xx.ravel(),yy.ravel()]#ravel方法将多维数组展平成一维数组，np.c_将下x,y的坐标一维数组组合成一个形状为（N，2）的数组，
                               #其中N是网格中点的数量。
colors=np.array(["#377eb8","#ff7f00"])
#可视化
fig=plt.figure(figsize=(8,12))
plot_idx=1#表明图片位置
for idx,X in enumerate(datasets):
    X=np.concatenate([X,X_outliers],axis=0)
    
    for algorithm in anomaly_algorithms:
        algorithm.fit(X)#先对样本数据进行拟合
        y_pred = algorithm.fit(X).predict(X)#之后预测数据点是否为异常值
        
        ax=fig.add_subplot(4,3,plot_idx);plot_idx+=1
        Z=algorithm.predict(xy)
        Z=Z.reshape(xx.shape)
        #绘制边界
        ax.contour(xx,yy,Z,levels=[0],
                    linewidths=2,colors="black")
        #绘制散点数据集
        ax.scatter(X[:,0],X[:,1],s=10,
                   #用两种不同颜色进行分别
                    color=colors[(y_pred+1)//2])
        ax.set_xlim(-7,7);ax.set_ylim(-7,7)
        ax.set_xticks([]);ax.set_yticks([])

结果：

从代码与最后的可视化情况来看，我们了解到为同意样本数据由三种不同方法进行处理。

拆分数据

简单介绍：

1. 在机器学习中数据集分成两种一是训练集，二是测试集。
2. 下面使用鸢尾花数据来实现数据的拆分。

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import seaborn as sns

X,y=load_iris(return_X_y=True)

X_train,X_test,y_train,y_test = train_test_split(
    X,y,test_size=0.2)#将数据集分别分成训练集和测试集

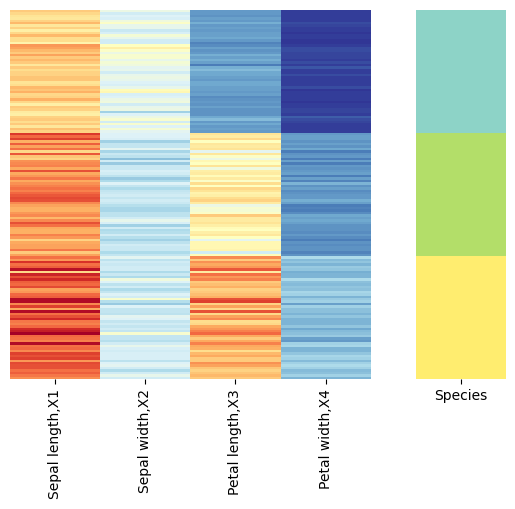
#可视化函数
def visualize(df):
    fig,axs=plt.subplots(1,2,
            #设置宽度比例，要求第一图宽度比例是二图的4倍
            gridspec_kw={'width_ratios':[4,1]})
    sns.heatmap(df.iloc[:,0:-1],
                cmap='RdYlBu_r',yticklabels=False,
                cbar=False,ax=axs[0])
    sns.heatmap(df.iloc[:,[-1]],
                cmap='Set3',yticklabels=False,
                cbar=False,ax=axs[1])

columns=['Sepal length,X1','Sepal width,X2',
         'Petal length,X3','Petal width,X4',
         'Species']
df_full=pd.DataFrame(np.c_[X,y],columns=columns)
visualize(df_full)

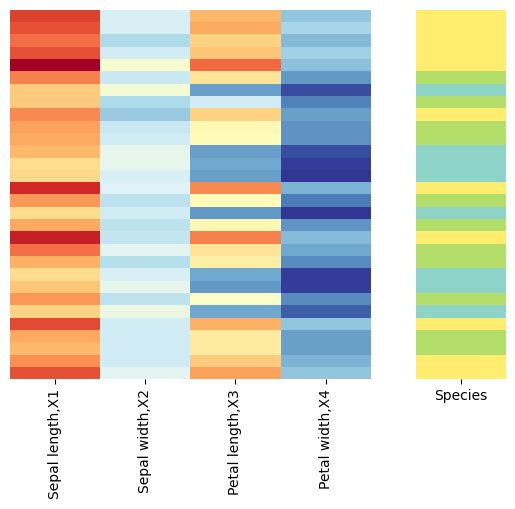
df_train=pd.DataFrame(np.c_[X_train,y_train],columns=columns)
df_test=pd.DataFrame(np.c_[X_test,y_test],columns=columns)

visualize(df_test)

结果：

多项式回归

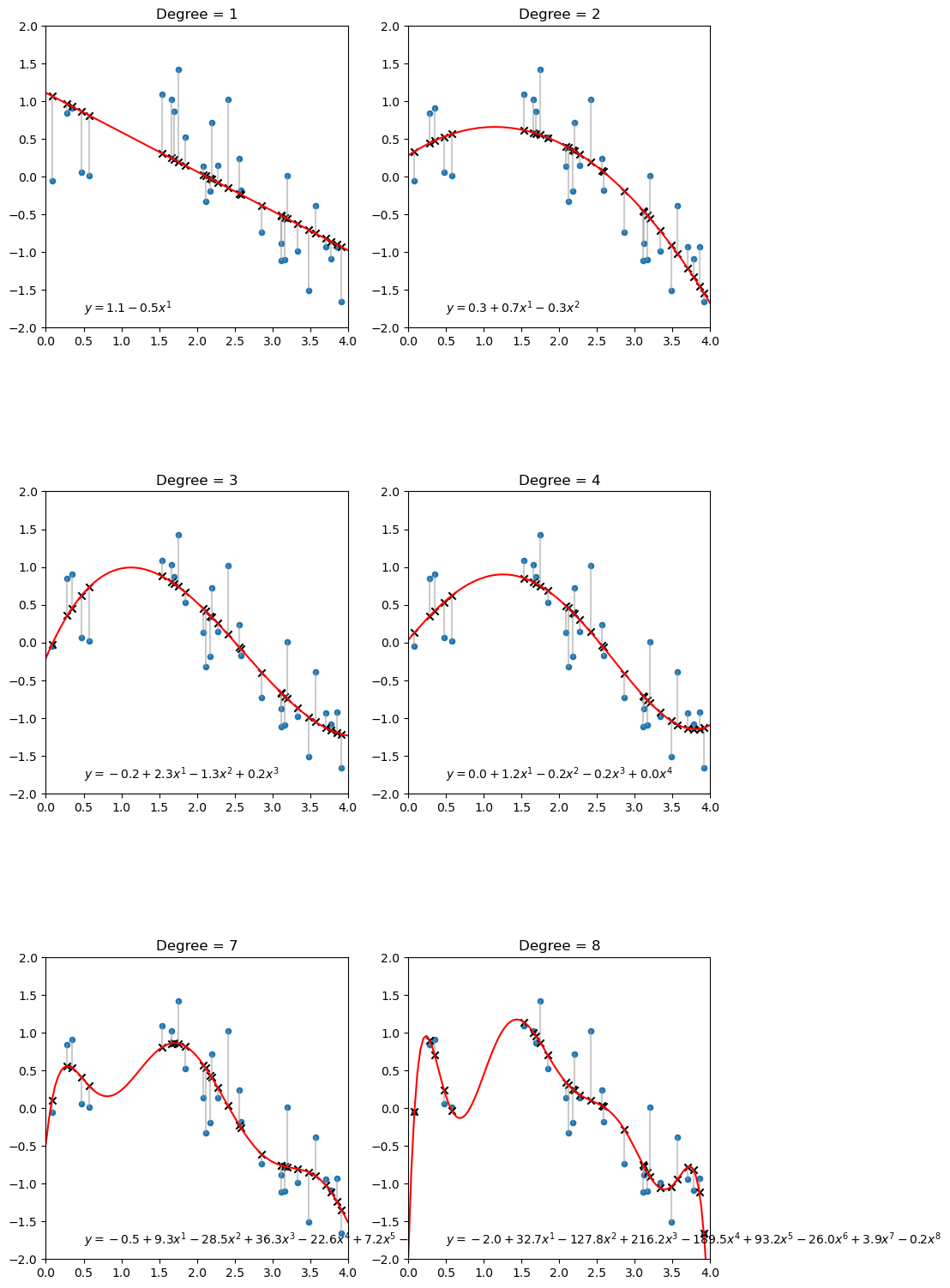
简单介绍

1. 是一种线性回归的扩展，允许我们通过引入多项式来建模非线性关系。
2. 从数据角度看，原本单一特征数据，利用简单数学运算，便能获得多特征数据。
3. 从函数角度看，多项式回归模型好比若干曲线叠加的结果。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
#PolynomialFeatures 通过设置特定的阶数来生成不同阶数的多项式特征
from sklearn.linear_model import LinearRegression

#生成随机数
np.random.seed(0)
num=30
X = np.random.uniform(0,4,num)
y = np.sin(0.4*np.pi*X) + 0.4 * np.random.randn(num)
data = np.column_stack([X,y])

x_array = np.linspace(0,4,101).reshape(-1,1)
degree_array = [1,2,3,4,7,8]
fig,axes=plt.subplots(3,2,figsize=(10,20))
axes=axes.flatten()

for ax,degree_idx in zip(axes,degree_array):
    #生成多项式回归的最高阶数
    poly = PolynomialFeatures(degree = degree_idx)
    #这里将一维数据X进行形状变换，转换成一个二位数组。列数为1，每行一个样本，每列一个特征
    X_poly = poly.fit_transform(X.reshape(-1,1))

    #训练线性回归模型
    poly_reg = LinearRegression()
    #开始加载数据，进行训练
    poly_reg.fit(X_poly,y)

    #进行预测
    y_poly_pred = poly_reg.predict(X_poly)
    data_ = np.column_stack([X,y_poly_pred])
    
    #主要对x_array运用模型进行预测
    y_array_pred = poly_reg.predict(poly.fit_transform(x_array))

    #绘制散点图
    ax.scatter(X,y,s=20)
    ax.scatter(X,y_poly_pred,marker='x',color='k')
    ax.plot(([i for (i,j) in data_ ],[i for (i,j) in data]),
            ([j for (i,j) in data_ ],[j for (i,j) in data]),
                c=[0.6,0.6,0.6],alpha = 0.5)
    ax.plot(x_array,y_array_pred,color='r')
    ax.set_title('Degree = %d'% degree_idx)

    #提取参数
    coef = poly_reg.coef_
    intercept = poly_reg.intercept_
    #回归解析式
    equation = '$y={:.1f}'.format(intercept)
    for j in range(1,len(coef)):
        equation += ' + {:.1f}x^{}'.format(coef[j],j)
    equation += '$'
    equation = equation.replace("+ -","-")
    #标注位置，使用text()函数其中参数为坐标
    ax.text(0.5,-1.8,equation)
    ax.set_aspect('equal',adjustable='box')
    ax.set_xlim(0,4)
    ax.grid(False)
    ax.set_ylim(-2,2)

结果：

正则化：抑制过度拟合

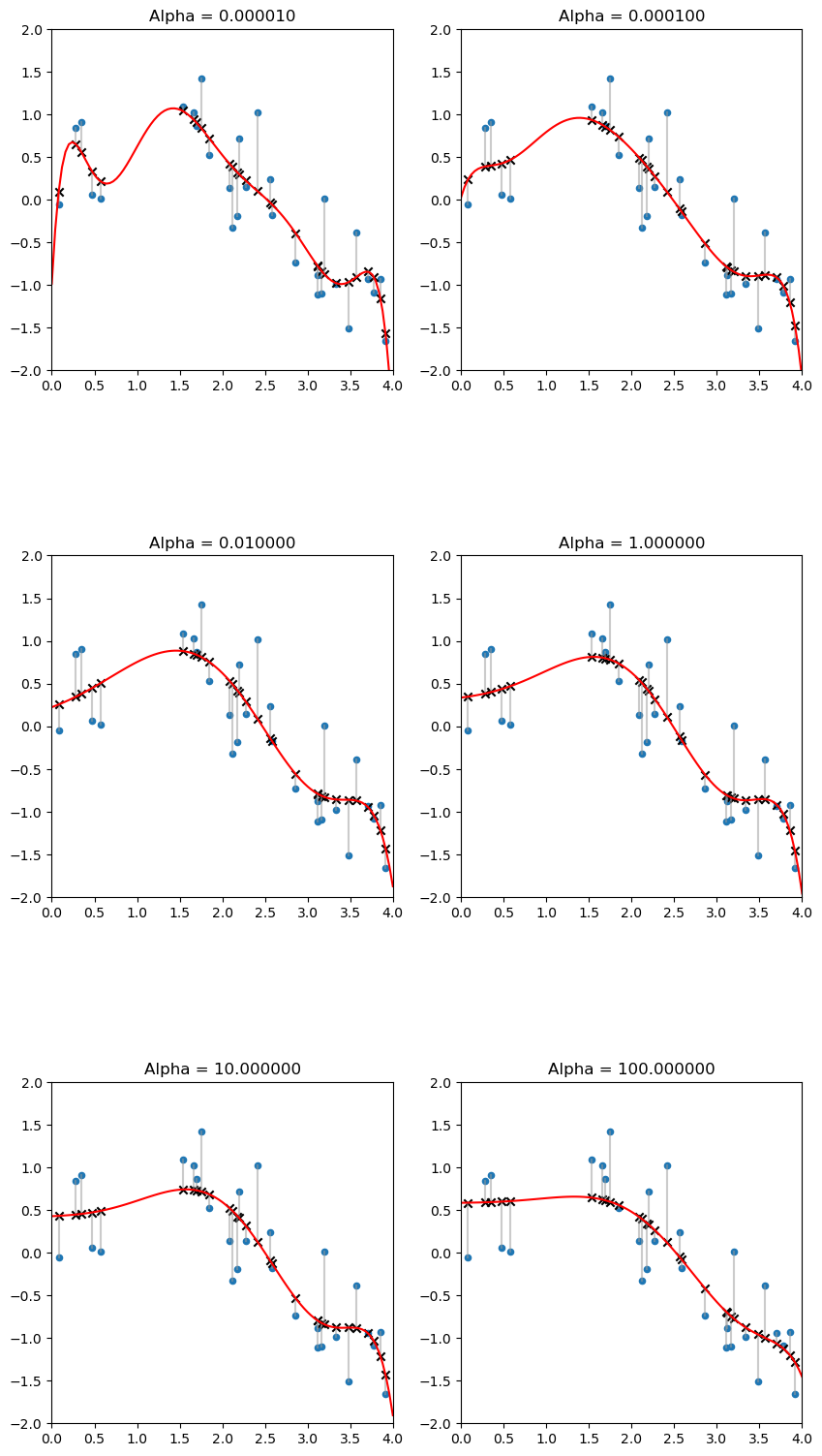
简单介绍

1. 正则化可以用来抑制过度拟合，正则项加在目标函数当中，让估计参数变小。
2. 正则化有两种，一种L2正则化，也叫岭正则化；还有一种是L1正则化叫做索套正则化。其中L2有助于减小模型参数大小，L1会将某些参数缩减为零。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import Ridge
#Ridge可用来完成岭回归

#生成随机数
np.random.seed(0)
num=30
X=np.random.uniform(0,4,num)
y=np.sin(0.4*np.pi*X) + 0.4 * np.random.randn(num)
data=np.column_stack([X,y])
x_array=np.linspace(0,4,101).reshape(-1,1)

#产生Polynomialfeatures对象用来进行多项式特征扩展
degree=8
ploy = PolynomialFeatures(degree = degree)
X_ploy=ploy.fit_transform(X.reshape(-1,1))

fig,axes=plt.subplots(3,2,figsize=(10,20))
axes=axes.flatten()

#惩罚因子
alpha_array = [0.00001,0.0001,0.01,1,10,100]
for ax,alpha_idx in zip(axes,alpha_array):
    #训练岭回归模型
    ridge=Ridge(alpha=alpha_idx)
    ridge.fit(X_poly,y.reshape(-1,1))

    #开始预测
    y_array_pred = ridge.predict(poly.fit_transform(x_array))
    y_poly_pred = ridge.predict(X_poly)
    data_ = np.column_stack([X,y_poly_pred])

    #绘制散点图
    ax.scatter(X,y,s=20)
    ax.scatter(X,y_poly_pred,marker='x',color='k')
    #绘制残差
    ax.plot(([i for (i,j) in data_],[i for (i,j) in data]),
            ([j for (i,j) in data_],[j for (i,j) in data]),
            c=[0.6,0.6,0.6],alpha=0.5)
    ax.plot(x_array,y_array_pred,color='r')
    ax.set_title('Alpha = %f'% alpha_idx)

    #提取参数
    coef = ridge.coef_[0]
    intercept = ridge.intercept_[0]
    ax.set_aspect('equal',adjustable='box')
    ax.set_xlim(0,4);ax.set_ylim(-2,2);ax.grid(False)

结果：