ZCMU-1051

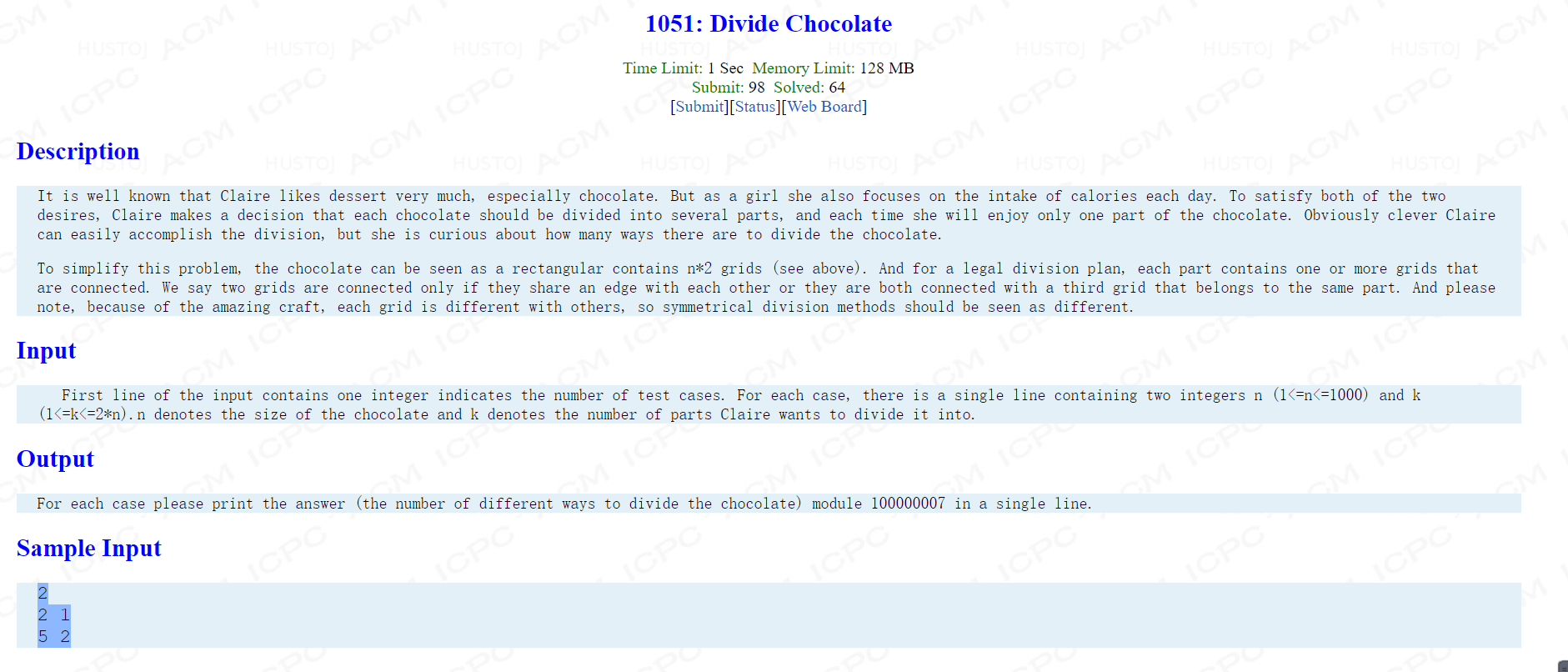
比较来说不太难其实,当然找到一定的公式这与前面的1033相识，都会用到f(i,j)=f(i-1,j)+f(i-1,j-1)

我们可以先从小部分看出来，一层可以整体或者两部分，在面对第i层看前面i-1层中分成j-1分和j分,但是又因为自己可以分成分开与不分开所以要用到三维数组，分别放置不分开与分开

---

我觉得比较难的点在于讨论i-1层与i层相连接的就是f(i,j)=g(f(i-1,j),f(i-1,j-1)),后面还要讨论一下j-2；对这样问题可以画出i-1的情况,与i层其余不看。以小看大。

---

#include<stdio.h>
#define mod 100000007
int dp[1002][2002][2]={0};
//对i列分成j部分的数组表示操作
//dp这类问题表示i中找j; 
void init(){
    int i,j,k;
    //其中又可以分成两部分，当前要不要分开
       
    dp[1][1][0]=1;
    dp[1][2][1]=1;
    //一行下分开后只能是2；
    for(i=2;i<1002;i++){
        dp[i][1][0]=1;
        //一个整体
         
        //因为分个数且每层两份，且题目也告诉了要2*n 
        for(j=2;j<2002;j++){
            dp[i][j][0] += dp[i-1][j][0];
            dp[i][j][0] %= mod;
            //表示在前面已经分号j分 
            dp[i][j][0] += dp[i-1][j-1][0];
            dp[i][j][0] %= mod;
            //分好j-1分，加上自己 
            dp[i][j][0] += 2*dp[i-1][j][1];
            dp[i][j][0] %= mod;
            //因为当前没分成两份，前一行分成两个，所以
            //i行怼上去后要乘以2； 
            dp[i][j][0] += dp[i-1][j-1][1];
            dp[i][j][0] %= mod;
            //虽然分成两行但只是j-1分 
            dp[i][j][1] += 2*dp[i-1][j-1][0];
            dp[i][j][1] %= mod;
            //当前分开不同怼上去 
            dp[i][j][1] += 2*dp[i-1][j-1][1];
            dp[i][j][1] %= mod;
            //一个怼（因为前面只有j-1） 
            dp[i][j][1] += dp[i-1][j][1];
            dp[i][j][1] %= mod;
            //因为要相对不会出现交叉 
            dp[i][j][1] += dp[i-1][j-2][0];
            dp[i][j][1] %= mod;
            //自己提供两种 
            dp[i][j][1] += dp[i-1][j-2][1];
            dp[i][j][1] %= mod;
        }
    }
}
 
int main(){
    int k,n,t;
    scanf("%d",&t);
    init();
    while(t--){
        scanf("%d%d",&n,&k);
        printf("%d\n",(dp[n][k][0]+dp[n][k][1])%mod);
    }
    return 0; 
}

借鉴观看代码