二叉搜索树

树

二叉搜索树
AVL树
红黑树
线段树 - with min/max/sum range queries examples
芬威克树/Fenwick Tree (Binary Indexed Tree)

 

在计算机科学中, 树(tree) 是一种广泛使用的抽象数据类型(ADT)— 或实现此ADT的数据结构 — 模拟分层树结构, 具有根节点和有父节点的子树,表示为一组链接节点。

树可以被(本地地)递归定义为一个(始于一个根节点的)节点集, 每个节点都是一个包含了值的数据结构, 除了值,还有该节点的节点引用列表(子节点)一起。 树的节点之间没有引用重复的约束。

一棵简单的无序树; 在下图中:

标记为7的节点具有两个子节点, 标记为2和6; 一个父节点,标记为2,作为根节点, 在顶部,没有父节点。

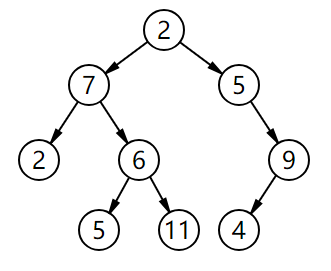
二叉搜索树

在计算机科学中，二叉树（BST）有时也被叫做有序二叉树或者排序二叉树是一种特别的容器类型：是一种储存数据到内存中的数据结构。二叉树允许快速查找，添加和删除元素，而且不仅可以被用于实现动态数据集，而且在查找数据表的时候可以允许通过key来查找一个元素。

二叉查找树会保持节点的key是排好序的，因此做查找或者其他操作的时候可以使用二分法：当在树中查找一个key的时候（或者插入一个新key），从根节点到叶子结点遍历一遍，对于节点中的key做比较，基于比较的结果，来决定在左或右子树中继续查找。平均情况下，这就意味着每一次比较都跳过了树结构的一半节点，所以每一次查找，插入或者删除所消耗的时间都和树中储存的数据量成対数关系。这样查找数据比在没有排序的数组中线性查找要快得多，但是比哈希表中相应的操作要慢。

一个有9个节点3层的二叉查找树，8是根节点。叶子节点没有画出来。

基础操作的伪代码

插入

insert(value)
  Pre: value has passed custom type checks for type T
  Post: value has been placed in the correct location in the tree
  if root = ø
    root ← node(value)
  else
    insertNode(root, value)
  end if
end insert

下面是注释：

insert(value)
  Pre: value has passed custom type checks for type T
  Post: value has been placed in the correct location in the tree
  //value事先已经通过自定义类型检测
  //然后value值被插入到树中正确的位置
  if root = ø//如果根节点是空节点
    root ← node(value)//将value新建的新节点直接赋给根节点
  else//调用insertNode将value插入树中
    insertNode(root, value)
  end if
end insert

insertNode：

insertNode(current, value)
  Pre: current is the node to start from
  Post: value has been placed in the correct location in the tree
  if value < current.value
    if current.left = ø
      current.left ← node(value)
    else
      InsertNode(current.left, value)
    end if
  else
    if current.right = ø
      current.right ← node(value)
    else
      InsertNode(current.right, value)
    end if
  end if
end insertNode

下面是注释：

insertNode(current, value)
  Pre: current is the node to start from
  Post: value has been placed in the correct location in the tree
  //current是根节点
  //value会被插入到树中正确位置
  if value < current.value//如果value小于当前节点的value
    if current.left = ø//如果当前节点的左子节点为空节点
      current.left ← node(value)//将value对应的新节点赋值给当前节点的左子节点
    else//如果当前节点的左子节点不为空，就递归调用InsertNode继续处理
      InsertNode(current.left, value)
    end if
  else//如果value大于或等于当前节点的value
    if current.right = ø//如果当前节点的右子节点为空节点
      current.right ← node(value)//将value对应的新节点赋值给当前节点的右子节点
    else//如果当前节点的右子节点不为空
      InsertNode(current.right, value)//递归调用InsertNode继续处理
    end if
  end if
end insertNode

查找

contains(root, value)
  Pre: root is the root node of the tree, value is what we would like to locate
  Post: value is either located or not
  if root = ø
    return false
  end if
  if root.value = value
    return true
  else if value < root.value
    return contains(root.left, value)
  else
    return contains(root.right, value)
  end if
end contains

下面是注释

contains(root, value)
  Pre: root is the root node of the tree, value is what we would like to locate
  Post: value is either located or not
  //root一开始是根节点，value是要查找的节点的值
  //结果返回是否包含value对应节点的真假值
  if root = ø//如果root是空节点，返回false
    return false
  end if
  if root.value = value//如果root的value与value相等，返回true
    return true
  else if value < root.value//如果value小于root.value，那就递归调用contains继续查询root的左子树
    return contains(root.left, value)
  else//如果value大于等于root.value，递归调用contains继续查询root的右子树
    return contains(root.right, value)
  end if
end contains

删除

remove(value)
  Pre: value is the value of the node to remove, root is the node of the BST
      count is the number of items in the BST
  Post: node with value is removed if found in which case yields true, otherwise false
  nodeToRemove ← findNode(value)
  if nodeToRemove = ø
    return false
  end if
  parent ← findParent(value)
  if count = 1
    root ← ø
  else if nodeToRemove.left = ø and nodeToRemove.right = ø
    if nodeToRemove.value < parent.value
      parent.left ←  nodeToRemove.right
    else
      parent.right ← nodeToRemove.right
    end if
  else if nodeToRemove.left = ø and nodeToRemove.right = ø
   if nodeToRemove.value < parent.value
     parent.left ←  nodeToRemove.left
   else
     parent.right ← nodeToRemove.left
   end if
  else
   largestValue ← nodeToRemove.left
   while largestValue.right = ø
     largestValue ← largestValue.right
   end while
   findParent(largestValue.value).right ← ø
   nodeToRemove.value ← largestValue.value
  end if
  count ← count - 1
  return true
end remove

下面是注释：

remove(value)
  Pre: value is the value of the node to remove, root is the node of the BST
      count is the number of items in the BST
  Post: node with value is removed if found in which case yields true, otherwise false
  //value是需要被删除的节点的值，root一开始是根节点，count是整个树的节点个数
  //如果找到了value对应的节点就删除然后返回true，否则false
  nodeToRemove ← findNode(value)//调用findNode找到要删除的节点存为nodeToRemove
  if nodeToRemove = ø//如果要删除的节点是空节点，删除失败，返回false
    return false
  end if
  parent ← findParent(value)//找到value值的父节点
  if count = 1//如果树只有一个节点，就把根节点赋值为空节点
    root ← ø
  else if nodeToRemove.left = ø and nodeToRemove.right = ø//如果要删除的节点是叶子结点
    if nodeToRemove.value < parent.value//如果要删除节点的值小于父节点的值，说明是父节点的左子节点
      parent.left ←  nodeToRemove.right//父节点的左子节点赋值为空节点
    else//如果要删除节点是父节点的右子节点，就将父节点的右子节点赋值为空节点
      parent.right ← nodeToRemove.right
    end if
  else if nodeToRemove.left = ø and nodeToRemove.right = ø//如果要删除的节点是叶子结点
   if nodeToRemove.value < parent.value
     parent.left ←  nodeToRemove.left
   else
     parent.right ← nodeToRemove.left
   end if
  else//如果要删除的节点既不是根节点也不是叶子节点
   largestValue ← nodeToRemove.left//要删除节点的左子节点
   while largestValue.right = ø
   //如果要删除节点的左子节点的右子节点不为空节点，就循环，一直找到nodeToRemove的左子树的最大节点
     largestValue ← largestValue.right
   end while
   findParent(largestValue.value).right ← ø//nodeToRemove的左子树的最大节点的父节点的右子节点赋值为空节点
   nodeToRemove.value ← largestValue.value//让后将nodeToRemove的左子树的最大节点赋值给要删除的节点
  end if
  count ← count - 1//树的长度减1
  return true//删除成功，返回true
end remove

查找节点的父节点

findParent(value, root)
  Pre: value is the value of the node we want to find the parent of
       root is the root node of the BST and is != ø
  Post: a reference to the prent node of value if found; otherwise ø
  if value = root.value
    return ø
  end if
  if value < root.value
    if root.left = ø
      return ø
    else if root.left.value = value
      return root
    else
      return findParent(value, root.left)
    end if
  else
    if root.right = ø
      return ø
    else if root.right.value = value
      return root
    else
      return findParent(value, root.right)
    end if
  end if
end findParent

下面是注释：

findParent(value, root)
  Pre: value is the value of the node we want to find the parent of
       root is the root node of the BST and is != ø
  Post: a reference to the prent node of value if found; otherwise ø
  //value是想要找到对应节点的父节点的那个节点的值，root是根节点
  //如果找到了给定值对应节点的父节点就返回那个父节点的引用，否则返回空节点
  if value = root.value//如果value对应节点是根节点，根节点没有父节点，所以返回空节点
    return ø
  end if
  if value < root.value//如果value小于根节点value，说明value对应节点在根节点的左子树
    if root.left = ø//如果根节点的左子节点为空节点，那什么都找不到，返回空节点
      return ø
    else if root.left.value = value//如果根节点的左子节点的值和value相等，说明value对应节点的父节点就是根节点，返回根节点
      return root
    else//否则递归调用继续往下寻找
      return findParent(value, root.left)
    end if
  else//value大于根节点value，value对应节点在根节点的右子树
    if root.right = ø//如果根节点的右子节点为空节点，那什么都找不到，返回空节点
      return ø
    else if root.right.value = value//如果根节点的右子节点的值和value想的，说明value对应节点的父节点就是根节点，直接返回根节点
      return root
    else//否则，递归调用继续往下寻找
      return findParent(value, root.right)
    end if
  end if
end findParent

查找节点

findNode(root, value)
  Pre: value is the value of the node we want to find the parent of
       root is the root node of the BST
  Post: a reference to the node of value if found; otherwise ø
  if root = ø
    return ø
  end if
  if root.value = value
    return root
  else if value < root.value
    return findNode(root.left, value)
  else
    return findNode(root.right, value)
  end if
end findNode

下面是注释

findNode(root, value)
  Pre: value is the value of the node we want to find the parent of
       root is the root node of the BST
  Post: a reference to the node of value if found; otherwise ø
  //value是想要查找的节点的值，root是根节点
  //返回找到的节点的引用，否则返回空节点
  if root = ø//如果根节点是空节点，直接返回空节点
    return ø
  end if
  if root.value = value//如果根节点的值和value相等，返回根节点
    return root
  else if value < root.value//如果value小于根节点value，说明value在左子树
    return findNode(root.left, value)//递归调用查找左子树
  else//如果value大于根节点value，说明value在左子树
    return findNode(root.right, value)//递归调用查找右子树
  end if
end findNode

查找最小节点

findMin(root)
  Pre: root is the root node of the BST
    root = ø
  Post: the smallest value in the BST is located
  if root.left = ø
    return root.value
  end if
  findMin(root.left)
end findMin

下面是注释

findMin(root)
Pre: root is the root node of the BST
  root = ø
Post: the smallest value in the BST is located
//root是二叉树的根节点
//返回二叉树的最小值
if root.left = ø//如果当前节点的左子节点是空节点，返回当前节点的值
  return root.value
end if
findMin(root.left)//否则递归调用findMin继续往左子树寻找s
end findMin

查找最大节点

findMax(root)
  Pre: root is the root node of the BST
    root = ø
  Post: the largest value in the BST is located
  if root.right = ø
    return root.value
  end if
  findMax(root.right)
end findMax

下面是注释

findMax(root)
  Pre: root is the root node of the BST
    root = ø
  Post: the largest value in the BST is located
  //root起始值是根节点
  //返回二叉树最大节点
  if root.right = ø//如果当前节点的右子树为空节点，返回当前节点的值
    return root.value
  end if
  findMax(root.right)//否则递归调用findMax继续查找右子树
end findMax

遍历

中序遍历

inorder(root)
  Pre: root is the root node of the BST
  Post: the nodes in the BST have been visited in inorder
  if root = ø
    inorder(root.left)
    yield root.value
    inorder(root.right)
  end if
end inorder

下面是注释

inorder(root)
  Pre: root is the root node of the BST
  Post: the nodes in the BST have been visited in inorder
  //root起始值是二叉树的根节点
  //中序遍历

  if root = ø//如果当前根节点是空节点
    inorder(root.left)//递归调用inorder遍历左子树
    yield root.value//生成当前节点的值
    inorder(root.right)//递归调用inorder遍历右子树
  end if
end inorder

前序遍历

preorder(root)
  Pre: root is the root node of the BST
  Post: the nodes in the BST have been visited in preorder
  if root = ø
    yield root.value
    preorder(root.left)
    preorder(root.right)
  end if
end preorder

下面是注释

preorder(root)
  Pre: root is the root node of the BST
  Post: the nodes in the BST have been visited in preorder
  //root是当前根节点
  //前序遍历
  if root = ø//如果当前根节点是空节点
    yield root.value//生成当前节点的值
    preorder(root.left)//递归调用preorder遍历左子树
    preorder(root.right)//递归调用preorder遍历右子树
  end if
end preorder

后序遍历

postorder(root)
  Pre: root is the root node of the BST
  Post: the nodes in the BST have been visited in postorder
  if root = ø
    postorder(root.left)
    postorder(root.right)
    yield root.value
  end if
end postorder

下面是注释

postorder(root)
  Pre: root is the root node of the BST
  Post: the nodes in the BST have been visited in postorder
  //root是当前根节点
  //后序遍历
  if root = ø//如果当前根节点是空节点
    postorder(root.left)//递归调用后序遍历当前节点的左子树
    postorder(root.right)//递归调用后序遍历当前节点的右子树
    yield root.value//生成当前根节点的值
  end if
end postorder

复杂度

时间复杂度

获取：O(log(n))

查询：O(log(n))

插入：O(log(n))

删除：O(log(n))

空间复杂度

O(n)

代码实现

BinaryTreeNode.js

import Comparator from '../../utils/comparator/Comparator';
import HashTable from '../hash-table/HashTable';

export default class BinaryTreeNode {//二叉树节点类
  /**
   * @param {*} [value] - node value.
   */
  constructor(value = null) {//构造函数，value是新节点的值
    this.left = null;//新节点的左子节点是null
    this.right = null;//新节点的右子节点是null
    this.parent = null;//新节点的父节点是null
    this.value = value;//新节点的值

    // Any node related meta information may be stored here.
    this.meta = new HashTable();
    //节点相关联的原信息存储在meta里，是一个哈希表

    // This comparator is used to compare binary tree nodes with each other.
    this.nodeComparator = new Comparator();
    //比较工具方法
  }

  /**
   * @return {number}
   */
  get leftHeight() {//leftHeight属性的getter
    if (!this.left) {//如果没有左子节点，返回0
      return 0;
    }

    return this.left.height + 1;//否则返回左子节点的height加1
  }

  /**
   * @return {number}
   */
  get rightHeight() {//rightHeight属性的getter
    if (!this.right) {//如果没有右子节点，返回0
      return 0;
    }

    return this.right.height + 1;//否则返回右子节点的height加1
  }

  /**
   * @return {number}
   */
  get height() {//height属性的getter
    return Math.max(this.leftHeight, this.rightHeight);
    //返回leftHeight和rightHeight中最大的那个值
  }

  /**
   * @return {number}
   */
  get balanceFactor() {//balanceFactor平衡因子属性的getter
    //平衡因子等于leftHeight减去rightHeight
    return this.leftHeight - this.rightHeight;
  }

  /**
   * Get parent's sibling if it exists.
   * @return {BinaryTreeNode}
   */
  get uncle() {//获取父节点的兄弟节点如果存在的话
    // Check if current node has parent.
    if (!this.parent) {//如果当前节点没有父节点，返回undefined
      return undefined;
    }

    // Check if current node has grand-parent.
    if (!this.parent.parent) {//如果当前节点没有爷爷节点，如果没有，返回undefined
      return undefined;
    }

    // Check if grand-parent has two children.
    //判断爷爷节点有没有两个子节点，如果没有就返回undefined
    if (!this.parent.parent.left || !this.parent.parent.right) {
      return undefined;
    }

    // So for now we know that current node has grand-parent and this
    // grand-parent has two children. Let's find out who is the uncle.
    if (this.nodeComparator.equal(this.parent, this.parent.parent.left)) {
      //用比较工具方法比较，如果父节点是爷爷节点的左子节点，就返回爷爷节点的右子节点
      // Right one is an uncle.
      return this.parent.parent.right;
    }

    // Left one is an uncle.
    return this.parent.parent.left;//否则返回爷爷节点的左子节点
  }

  /**
   * @param {*} value
   * @return {BinaryTreeNode}
   */
  setValue(value) {//设置当前节点的值
    this.value = value;

    return this;
  }

  /**
   * @param {BinaryTreeNode} node
   * @return {BinaryTreeNode}
   */
  setLeft(node) {//设置当前节点的左子节点
    // Reset parent for left node since it is going to be detached.
    if (this.left) {//如果有左子节点，左子节点的parent设置为null
      this.left.parent = null;
    }

    // Attach new node to the left.
    this.left = node;//设置新的左子节点

    // Make current node to be a parent for new left one.
    if (this.left) {//新左子节点的parent赋值
      this.left.parent = this;
    }

    return this;
  }

  /**
   * @param {BinaryTreeNode} node
   * @return {BinaryTreeNode}
   */
  setRight(node) {//设置当前节点的右子节点
    // Reset parent for right node since it is going to be detached.
    if (this.right) {//如果有右子节点，右子节点的parent设置为null
      this.right.parent = null;
    }

    // Attach new node to the right.
    this.right = node;//设置新的右子节点

    // Make current node to be a parent for new right one.
    if (node) {//新右子节点的parent赋值
      this.right.parent = this;
    }

    return this;
  }

  /**
   * @param {BinaryTreeNode} nodeToRemove
   * @return {boolean}
   */
  removeChild(nodeToRemove) {//删除子节点
    if (this.left && this.nodeComparator.equal(this.left, nodeToRemove)) {
      //如果左子节点是要删除的节点，this.left设置为null
      this.left = null;
      return true;
    }

    if (this.right && this.nodeComparator.equal(this.right, nodeToRemove)) {
      //如果右子节点是要删除的节点，this.right设置为null
      this.right = null;
      return true;
    }

    return false;
  }

  /**
   * @param {BinaryTreeNode} nodeToReplace
   * @param {BinaryTreeNode} replacementNode
   * @return {boolean}
   */
  replaceChild(nodeToReplace, replacementNode) {//替换子节点
    if (!nodeToReplace || !replacementNode) {//缺少参数，返回false
      return false;
    }

    if (this.left && this.nodeComparator.equal(this.left, nodeToReplace)) {//替换左子节点
      this.left = replacementNode;
      return true;
    }

    if (this.right && this.nodeComparator.equal(this.right, nodeToReplace)) {//替换右子节点
      this.right = replacementNode;
      return true;
    }

    return false;
  }

  /**
   * @param {BinaryTreeNode} sourceNode
   * @param {BinaryTreeNode} targetNode
   */
  static copyNode(sourceNode, targetNode) {//复制源节点到目标节点
    //调用目标节点的setValue，setLeft，setRight分别设置值，左子节点，和右子节点
    targetNode.setValue(sourceNode.value);
    targetNode.setLeft(sourceNode.left);
    targetNode.setRight(sourceNode.right);
  }

  /**
   * @return {*[]}
   */
  traverseInOrder() {//中序遍历，左 => 根 => 右，所有节点的值连接成一个数组返回
    let traverse = [];

    // Add left node.
    if (this.left) {//左子节点
      traverse = traverse.concat(this.left.traverseInOrder());
    }

    // Add root.
    traverse.push(this.value);//根节点

    // Add right node.
    if (this.right) {//右子节点
      traverse = traverse.concat(this.right.traverseInOrder());
    }

    return traverse;
  }

  /**
   * @return {string}
   */
  toString() {//中序遍历返回的数组字符串化
    return this.traverseInOrder().toString();
  }
}

BinarySearchTreeNode.js

import BinaryTreeNode from '../BinaryTreeNode';
import Comparator from '../../../utils/comparator/Comparator';

export default class BinarySearchTreeNode extends BinaryTreeNode {//二叉搜索树节点类，继承自二叉树节点类
  /**
   * @param {*} [value] - node value.
   * @param {function} [compareFunction] - comparator function for node values.
   */
  constructor(value = null, compareFunction = undefined) {
    super(value);//调用父类构造函数

    // This comparator is used to compare node values with each other.
    this.compareFunction = compareFunction;//自定义比较方法
    this.nodeValueComparator = new Comparator(compareFunction);//比较工具类
  }

  /**
   * @param {*} value
   * @return {BinarySearchTreeNode}
   */
  insert(value) {//插入指定值的节点
    if (this.nodeValueComparator.equal(this.value, null)) {
      //如果当前节点的值等于null，就把新value赋值给this.value
      this.value = value;

      return this;//返回当前二叉搜索树节点
    }

    if (this.nodeValueComparator.lessThan(value, this.value)) {
      //如果新value值小于大当前节点value值，那么新value值应该插入到左子树中
      // Insert to the left.
      if (this.left) {//如果当前节点有左子树，那么递归调用insert往左子树插入新value
        return this.left.insert(value);
      }

      const newNode = new BinarySearchTreeNode(value, this.compareFunction);
      //如果当前节点没有左子树，那么新建二叉搜索树节点，然后调用setLeft将新节点插入作为当前节点的左子节点
      this.setLeft(newNode);

      return newNode;
    }

    if (this.nodeValueComparator.greaterThan(value, this.value)) {
      //如果新value值大于当前节点value值，那么新value值应该插入到右子树中
      // Insert to the right.
      if (this.right) {//如果当前节点有右子树，那么递归调用insert往右子树插入新value
        return this.right.insert(value);
      }

      const newNode = new BinarySearchTreeNode(value, this.compareFunction);
      //如果当前节点没有右子树，那么新建二叉搜索树节点，然后调用setRight将新节点插入作为当前节点的右子节点
      this.setRight(newNode);

      return newNode;
    }

    return this;
  }

  /**
   * @param {*} value
   * @return {BinarySearchTreeNode}
   */
  find(value) {//查找指定值对应节点
    // Check the root.
    if (this.nodeValueComparator.equal(this.value, value)) {//如果指定值和当前节点值相等，返回
      return this;
    }

    if (this.nodeValueComparator.lessThan(value, this.value) && this.left) {
      //如果指定值小于当前节点值，且当前节点有左子树，就递归调用find去左子树查询
      // Check left nodes.
      return this.left.find(value);
    }

    if (this.nodeValueComparator.greaterThan(value, this.value) && this.right) {
      //如果指定值大于当前节点值，且当前节点有右子树，就递归调用find去右子树查询
      // Check right nodes.
      return this.right.find(value);
    }

    return null;
  }

  /**
   * @param {*} value
   * @return {boolean}
   */
  contains(value) {//判断是否当前节点包含了指定值对应的节点，也就是说是当前节点的子节点
    return !!this.find(value);
  }

  /**
   * @param {*} value
   * @return {boolean}
   */
  remove(value) {//删除指定值对应的节点
    const nodeToRemove = this.find(value);//找到要删除的节点

    if (!nodeToRemove) {//如果没有找到对应节点，抛出错误
      throw new Error('Item not found in the tree');
    }

    const { parent } = nodeToRemove;//要删除的节点的父节点

    if (!nodeToRemove.left && !nodeToRemove.right) {//如果要删除的节点是叶子节点，没有左右子节点
      // Node is a leaf and thus has no children.
      if (parent) {//如果要删除的节点有父节点，就让父节点删除掉这个子节点即可
        // Node has a parent. Just remove the pointer to this node from the parent.
        parent.removeChild(nodeToRemove);
      } else {//如果要删除的节点没有父节点，就将它的值赋为undefined
        // Node has no parent. Just erase current node value.
        nodeToRemove.setValue(undefined);
      }
    } else if (nodeToRemove.left && nodeToRemove.right) {
      //如果不是叶子节点，有左右子节点
      //那就在右子树中找到下一个大于当前节点的值然后替换
      // Node has two children.
      // Find the next biggest value (minimum value in the right branch)
      // and replace current value node with that next biggest value.
      const nextBiggerNode = nodeToRemove.right.findMin();//在当前节点的右子树中找到最小节点
      if (!this.nodeComparator.equal(nextBiggerNode, nodeToRemove.right)) {
        //如果右子树的最小节点和要删除的节点的右子节点不是同一个节点，那么就删掉右子树最小节点的值，给要删除节点赋值
        this.remove(nextBiggerNode.value);
        nodeToRemove.setValue(nextBiggerNode.value);
      } else {//如果右子树最小节点就是要删除的节点的右子节点，那么就直接将要删除的节点替换为其右子节点
        // In case if next right value is the next bigger one and it doesn't have left child
        // then just replace node that is going to be deleted with the right node.
        nodeToRemove.setValue(nodeToRemove.right.value);
        nodeToRemove.setRight(nodeToRemove.right.right);
      }
    } else {//如果不是叶子节点，只有一个子节点
      //就设置要删除节点的这个唯一的子节点为要删除节点的父节点的直接子节点
      // Node has only one child.
      // Make this child to be a direct child of current node's parent.
      /** @var BinarySearchTreeNode */
      const childNode = nodeToRemove.left || nodeToRemove.right;//要删除节点的唯一子节点

      if (parent) {//如果要删除节点有父节点
        parent.replaceChild(nodeToRemove, childNode);//直接替换成要删除节点的唯一子节点
      } else {//否则将唯一子节点复制到要删除节点的位置
        BinaryTreeNode.copyNode(childNode, nodeToRemove);
      }
    }

    // Clear the parent of removed node.
    nodeToRemove.parent = null;//断开被删除节点的父节点指针

    return true;
  }

  /**
   * @return {BinarySearchTreeNode}
   */
  findMin() {//找到当前节点的子节点中最小的节点，遍历左子树寻找
    if (!this.left) {
      return this;
    }

    return this.left.findMin();
  }
}

BinarySearchTree.js

import BinarySearchTreeNode from './BinarySearchTreeNode';

export default class BinarySearchTree {//二叉搜索树类
  /**
   * @param {function} [nodeValueCompareFunction]
   */
  constructor(nodeValueCompareFunction) {
    this.root = new BinarySearchTreeNode(null, nodeValueCompareFunction);//根节点

    // Steal node comparator from the root.
    this.nodeComparator = this.root.nodeComparator;//比较工具方法
  }

  /**
   * @param {*} value
   * @return {BinarySearchTreeNode}
   */
  insert(value) {//从根节点开始判断，插入新节点
    return this.root.insert(value);
  }

  /**
   * @param {*} value
   * @return {boolean}
   */
  contains(value) {//从根节点开始寻找是否包含某个节点
    return this.root.contains(value);
  }

  /**
   * @param {*} value
   * @return {boolean}
   */
  remove(value) {//从根节点开始寻找删除某个值对应节点
    return this.root.remove(value);
  }

  /**
   * @return {string}
   */
  toString() {//中序遍历后存入的数组字符串化
    return this.root.toString();
  }
}