零群论基础理解置换群、Pólya 定理和 Burnside 引理

2024/5/27 upd1: latex 修了。

2024/5/27 upd2: \(MSET_3\) 算错了 /(ㄒoㄒ)/~~，已修。

同步发表于校 OJ。

讲道理，这些东西是能用自然语言讲清楚的，搭配自然语言和公式能起到很好的理解效果。

本篇的主旨是通过简单形象的描述说清楚这两个巨头说的是什么东西，怎么直观较严谨证明。

同时使用的符号不是使人晕头转向的 \(A,B,X,Y\)，具有一致性和可读性。

或许需要的前置知识是一些生成函数的东西，会更加融会贯通一些。

建议先翻到最后阅读一下后记，了解你需要掌握什么之后再接着看。同时浏览文章长度以确定是否接着看。

群论

零群论基础，所以要补充一些群论知识，很合理吧！

其实只是稍微提一些概念，毕竟我们不需要晦涩难懂的证明。虽然下面或许有些东西无关，但是作为了解没有坏处。

而且也没有什么复杂的东西，连子群都讲不到。

一个群（group）是一个二元组 \((G,\cdot)\)，其中 \(\cdot\) 是一个定义在集合 \(G\) 上的二元运算，并满足以下性质：

• 封闭性（totality）：\(\forall a,b\in G, a\cdot b \in G\)。
• 结合律（associativity）：\(\forall a,b,c\in G, (a\cdot b)\cdot c=a\cdot(b\cdot c)\)。
• 单位元（identity）：\(\exists e\in G~~s.t.~~ \forall a\in G, e\cdot a=a\cdot e=a\)。单位元也叫幺元。
• 逆元（divisibility）：\(\forall a\in G,\exists b\in G ~~s.t.~~ a\cdot b=b\cdot a=e\)。此处 \(b\) 也记作 \(a^{-1}\)。

（\(s.t.\) 意为 such that，使得。）

这几条的指向都应该很明确，不用作过多解释。不是很理解的话有如下举例：

\((\mathbb Z,+)\) 是群，其中任意两个整数相加还是整数，加法具有结合律。单位元是 \(0\)，逆元为相反数。

\((\mathbb R,\times)\) 不是群，唯一不满足条件的是 \(0\) 没有逆元。

\((\{f(z)\in\mathbb F_n\mid[z^0]f(z)\not=0\},\times\pmod{z^n})\) 是群。其中任意两个 \(n\) 阶多项式乘起来取模还是一个 \(n\) 阶多项式，这一运算具有结合律，单位元是 \(1\)，逆元为多项式求逆。

然后有两个性质：

• 单位元唯一。考虑反证：设有两个不等单位元 \(e_1,e_2\)，则 \(e_1\cdot e_2=e_1=e_2\)，导出矛盾。

• 逆元唯一。考虑反证：设 \(x\) 有两个不等逆元 \(y_1,y_2\)，则 \((y_1\cdot x)\cdot y_2=y_1\cdot(x\cdot y_2)\Rightarrow e\cdot y_2=y_1\cdot e\Rightarrow y_1=y_2\)，导出矛盾。

• 除法：有且仅有一个 \(x~s.t.~x\cdot y=z\)。此时 \(x=z\cdot y^{-1}\)。

还有一些其他的或许没用的定义：

半群（semigroup）：只满足封闭性和结合律。

幺半群（monoid）：只满足封闭性、结合律和单位元。

阿贝尔群（Abelian group）：除了上述四条外还满足交换律（commutativity）

线段树所维护的内容是一个半群信息和一个幺半群懒标以及他们之间的运算。通过自定义结构体与其上的 operators 的方式可以得到一个「真·线段树模板」。详细解读参见这个 blog。

还有更多种类的群定义如下：

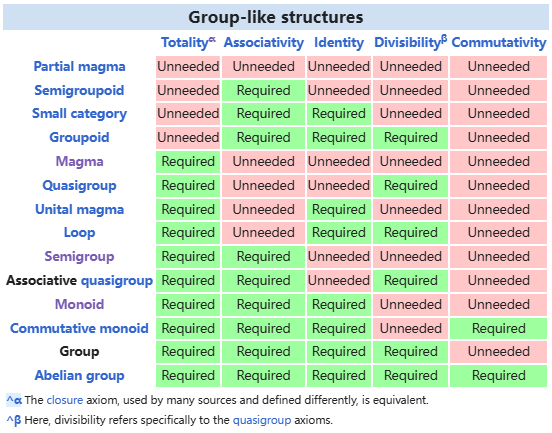
图源维基百科。颜色表示我在截图之前是否打开过这个页面（

群往上叠附加条件还有环域等定义，不过离题过远，不作介绍。感兴趣可以自行阅读维基。

到这里应该都是 naïve 的。

置换群

首先有一个大小为 \(m\) 的集合 \(M\)，定义一个置换是一个 \(M\to M\) 的双射。

双射，如果有人不知道的话，意思是函数（映射）的每一个因变量的值能唯一对应一个自变量的值。

我们可以直接把 \(M\) 看成集合 \(\{1,2,\dots,m\}\)，对于一个排列 \(\{a_m\}\)，一个置换可以表示为函数（映射） \(f(1)=a_1,\dots,f(m)=a_m\)。因为 \(a\) 是排列，所以 \(f\) 是双射，满足条件。

如果不想把置换看作一些元素的映射，也可以直接看作一个序列的变换，这一理解当然更直观：\([1,2,\dots,m]\to[a_1,a_2,\dots,a_m]\)。

这两种表示是等价的。

从上面的内容里不难看出，置换符合我们脑中对排列的理解，表示的就是对一系列元素的重排。

这里我没有使用那个复杂且吓人的两排括号记号，因为他没有意义。

我们定义两个置换之间的复合 \(f\circ g=g(f)\) 直接表示两个函数（映射）的复合，或者两个排列的复合，分别对应两种理解。注意到复合能成立 iff 两个置换的集合相同。

然后我们定义置换群。一个置换群就是一系列集合相同的置换和它们之间的复合构成的群。

结合律是显然的。

因为需要有单位元，所以一个置换群里必然包含恒等变换 \(f(x)=x\) 或排列 \([1,2,\dots,m]\)。

你还需要保证封闭性与逆元。（其实这里如果保证了封闭性就必然会有逆元，不深究。）

很多东西都是置换群。置换群用以描述同构关系。

这里千万不要单纯的把 \(M\) 看成那个 \(\mathbb Z~\cap~[1,m]\)，他可以是任何元素，也可以再映射回那个整数集合。

当然这两段话本身很抽象，可以看一些例子。

有 \(\circledR\triangle\aleph\) 三种形状排列在一个圆排列上，那么同构情况可以表示为

\[\newcommand{\sa}{\circledR} \newcommand{\sb}{\triangle} \newcommand{\sc}{\aleph} [\sa,\sb,\sc]=[\sb,\sc,\sa]=[\sc,\sa,\sb];\\ [\sa,\sc,\sb]=[\sc,\sb,\sa]=[\sb,\sa,\sc]; \]

你会发现这每一组对应置换群\(\left(\{[1,2,3],[2,3,1],[3,1,2]\},\circ\right)\)。

有 \(♠♣♡♢\) 四种形状排列在一个正方形的四个角上，那么有

\[\newcommand{\sa}{♠} \newcommand{\sb}{♣} \newcommand{\sc}{♡} \newcommand{\sd}{♢} ~~~~[\sa,\sb,\sc,\sd]=[\sb,\sc,\sd,\sa]=[\sc,\sd,\sa,\sb]=[\sb,\sc,\sd,\sa]\\ =[\sd,\sc,\sb,\sa]=[\sc,\sb,\sa,\sd]=[\sb,\sa,\sd,\sc]=[\sc,\sb,\sa,\sd] \]

以及另外两种不同的情况。可以发现这是两个顺序颠倒的圆排列的并。

有同学到这里可能还是云里雾里的。

解释上面的例子：

\[\newcommand{\sa}{♠} \newcommand{\sb}{♣} \newcommand{\sc}{♡} \newcommand{\sd}{♢} \begin{matrix} \sa & - & \sb & ~ & \sd & - & \sc \\ | & ~ & | & = & | & ~ & | \\ \sd & - & \sc & ~ & \sa & - & \sb \end{matrix} \]

易知上面两个正方形（虽然不太正）其实是同一个东西，只是沿水平轴翻转了 \(180^\circ\)，现在如果我们都用 左上-右上-右下-左上 的顺序提取出形状，可以得到 \(\newcommand{\sa}{♠} \newcommand{\sb}{♣} \newcommand{\sc}{♡} \newcommand{\sd}{♢}[\sa,\sb,\sc,\sd]=[\sd,\sc,\sb,\sa]\)。

同一个东西，同一个外观，不同的顺序，同构的来源。

置换群是对对称性的描述。

上面八种等价其实分别对应

• 不变
• 逆时针旋转 \(90^\circ\)
• 逆时针旋转 \(180^\circ\)
• 逆时针旋转 \(270^\circ\)
• 沿水平轴翻转 \(180^\circ\)
• 沿水平轴翻转 \(180^\circ\) 并逆时针旋转 \(90^\circ\)
• 沿水平轴翻转 \(180^\circ\) 并逆时针旋转 \(180^\circ\)
• 沿水平轴翻转 \(180^\circ\) 并逆时针旋转 \(270^\circ\)

另一种理解方式是，我们有两个“基操作”：沿水平轴翻转 \(180^\circ\) 和 逆时针旋转 \(90^\circ\)。为了满足封闭性，对他们进行线性组合，从 \((0,0)\) 到 \((1,3)\) 正好八种情况。

再之前那个例子也是一样，基操作只有一个：向右循环移位一次。

关于这个对称性更深入更形象的理解可以去看看 3b1b 的这个视频，有些内容是无关的，择优录取。

相信看完这个视频之后你能更加理解关于置换群和对称性的相关内容并领会数学之美。

总结：

1. 置换就是排列作用。
2. 置换群就是一系列置换的集合。
3. 置换群通常都描述了一种对称性。

有一点需要注意：以正方体的 3d 旋转为例，它的顶点、棱和面各自的对称关系是三个不同的置换群。我们的对称性实际上保证的是各个元素之间存在固定的关系，是超出几何关系之上的。

再多定义一个概念：对称群（symmetric group）。一个 \(n\) 阶对称群 \(S_n\) 包含了所有大小为 \(n\) 的置换，是一种特殊的置换群。

还有一个惊人的数学事实：凯莱定理（Cayley's theorem），说的是所有群都同构于置换群，这也是为什么那个视频一直在用置换群举例子。有兴趣的话可以去了解，这边也跳过。

Pólya 定理

为什么先讲这个？因为这个理解了之后 Burnside 引理就很好理解了。

注意这里的 Pólya 定理与大家所或许知道的那个不太一样。

下面的内容 powered by x义x 的 符号化方法相关笔记，另外这是神文。

前置概念

我们还是有之前那个集合 \(M=\{1,\dots,m\}\) 以及一个其上的置换群 \(G\)。取一个组合类 \(\mathcal B\)，我们将要研究集合 \(\mathcal B^M\)，即所有 \(M\to\mathcal B\) 的映射组成的集合。

什么是组合类？

这是符号化方法的基础。一个组合类（combinatorial class）是一个可数集合 \(\mathcal A\)，里面的元素是一些组合对象，比如有标号树，烯烃，被染色的环。

同时这个集合有一个附带的大小函数（size function） \(f:\mathcal A\to\mathbb N\)。比如节点数，序列长度或者碳原子个数等等说的就是大小函数。记 \(f(x)=|x|\)，或者，在某些需要指明组合类的场合下， \(|x|_{\mathcal A}\)。

对于自然数 \(n\)，再定义计数序列（counting sequence）\(A_n=|\{x\in\mathcal A,|x|=n\}|\)，意思是大小为 \(n\) 的元素数量。在此基础上可以定义这个组合类的 OGF 等。

更详细的理解可参考 x义x 那个文章的 20 页往后的内容。

在这里也可以简单地理解为一个集合，包含了组合对象的枚举。

回到上文。怎么理解这里的 \(\mathcal B^M\) 呢？我们称一个 \(M\to\mathcal B\) 的映射为一个染色方案。

这个名字的来历是 \(\mathcal B\) 为颜色集合的情形。容易知道这相当于给 \(M\) 中的每个元素分配一个 \(\mathcal B\) 中的颜色。

那么对于一般的情况，这个映射就是给 \(M\) 中的元素分别分配一个组合对象。

当然这么说不太好懂，我们来看两个例子。

无标号有根树计数。

设所有无标号有根树构成的组合类为 \(\mathcal T\)，其中大小函数定义为树的大小。计数时首先钦定根，然后枚举根节点出边数量设为 \(s\)，依次编号 \(1,\dots,s\)，为构成一棵树，每一个出边上都需要挂一棵无标号有根树。于是能自然定义 \(M=\{1,\dots,s\},\mathcal B=\mathcal T\)，而 \(G\) 表示的是 \(M\) 中元素的等价关系，这里由于子树间是无序的，于是 \(G\) 为 \(s\) 阶对称群 \(S_s\)。

再次强调，为什么这里一会赋编号一会又说等价，是因为实际的情况是这是相同对象的不同摆放方式用同样方法提取顺序得到的。而这里的提取顺序是编号 \(1,\dots,s\)，无论子树之间顺序怎么调换都从左往右提取，但是它们都是一棵树，于是全排列都与 \([1,\dots,s]\) 等价。

无标号基环树计数。

假如我们已经知道了所有无标号有根树构成的组合类为 \(\mathcal T\)，那么考虑基环树的生成方式：若干棵无标号有根树排列在一个环上。于是先枚举环大小设为 \(s\)，那么我们所需要的是给环上 \(M={1,\dots,s}\) 中的每一个元素赋一棵树，所以 \(\mathcal B=\mathcal T\)，而因为它们排列在环上，所以所有的旋转和翻转都对应同一种情况，有 \(G\) 为全部的长为 \(s\) 的循环移位与其逆序。

通过这两个例子应该能理解 \(\mathcal B\) 与 \(G\) 的意义。

为什么例子不放有标号的呢？有标号的情况我们可以通过钦定按编号顺序排列等方式容斥掉相同方案，那么 \(G\) 就是只包含恒等变换的 trivial 的情况，无法帮助理解。

我们称两个染色方案 \(\phi_1,\phi_2\) 本质相同，如果 \(\exists g\in G,\phi_1\circ g=\phi_2\)。称染色方案的等价类集合为 \(\mathcal B^M/G\)。

怎么理解呢？最直观的方法仍是将 \(\mathcal B\) 视为颜色集合 \(\{{\color{red}\bullet},{\color{blue}\bullet}\}\)。那么对于 \(G=S_3\)，有等价类

\[\newcommand{\q}{{\color{red}\bullet}} \newcommand{\b}{{\color{blue}\bullet}} \begin{aligned} &\q\q\q\\ &\b\q\q=\q\b\q=\q\q\b\\ &\b\b\q=\b\q\b=\q\b\b\\ &\b\b\b \end{aligned} \]

注：这里对映射的表示不直接。 \({\color{red}\bullet}{\color{blue}\bullet}{\color{red}\bullet}\) 应当表示映射 \(\phi(1)={\color{red}\bullet},\phi(2)={\color{blue}\bullet},\phi(3)={\color{red}\bullet}\)。

再比如 \(\mathcal B=\{{\color{red}\bullet},{\color{blue}\bullet},{\color{green}\bullet}\}\)，对于上面 T2 的 \(G|_{s=4}\)，染色方案 \({\color{red}\bullet}{\color{red}\bullet}{\color{green}\bullet}{\color{blue}\bullet}\) 所属的等价类为

\[\newcommand{\q}{{\color{red}\bullet}} \newcommand{\b}{{\color{blue}\bullet}} \newcommand{\f}{{\color{green}\bullet}} ~~~~\q\q\f\b=\q\f\b\q=\f\b\q\q=\b\q\q\f\\ =\b\f\q\q=\f\q\q\b=\q\q\b\f=\q\b\f\q \]

而染色方案 \({\color{red}\bullet}{\color{blue}\bullet}{\color{red}\bullet}{\color{blue}\bullet}\) 所属的等价类为

\[{\color{red}\bullet}{\color{blue}\bullet}{\color{red}\bullet}{\color{blue}\bullet} ={\color{blue}\bullet}{\color{red}\bullet}{\color{blue}\bullet}{\color{red}\bullet} \]

\(\mathcal B\) 中的每一个元素 \(\beta\) 有个权重 \(w(\beta)\)，一个映射（染色方案）的权重 \(w(\phi):=\prod_{k\in M}w(\phi(k))\)，显然同一个等价类中的映射权重都一样，不然不会等价，称为这个等价类的权重。

注意这里定义了两个函数，勿混淆。

注意这个权重函数没说值域，所以可以是一些奇怪的东西，比如一个幂级数。

而 Pólya 定理所计算的是每一个等价类的权重之和。这个该怎么理解呢？

每一个等价类的权重之和就是所有本质不同染色方案的权重之和。

回到刚才那个无标号有根树问题，我们定义 \(w(\beta)=z^{|\beta|}\)，那么 \(w(\phi)\) 的指数就是所有子树大小之和。我们会发现，每一种元素的组合对总大小贡献一次，每一个等价类的权重之和是幂级数 \(F\)，它的 \(z^n\) 项系数就是不重不漏所有整棵树大小为 \(n+1\)（加上根）的无标号有根树数量。

理解了这个例子，可以说你就理解了 Pólya 定理的目的。

Pólya 定理

Pólya 定理的内容如下：

\[\boxed{\sum_{\phi\in(\mathcal B^M/G)}w(\phi)=Z\left(G;\sum_{\beta\in\mathcal B}w(\beta),\dots,\sum_{\beta\in\mathcal B}w^m(\beta)\right)} \]

其中

\[\boxed{Z(G;x_1,\dots,x_m)=\dfrac 1{|G|}\sum_{g\in G}x_1^{j_1(g)}\dots x_m^{j_m(g)}} \]

其中 \(j_k(g)\) 表示 \(g\) 中大小为 \(k\) 的循环个数。（应该都知道循环吧。排列里面也叫置换环。对于 \(g=[1,3,2],j_1(g)=1,j_2(g)=1,j_3(g)=0\)。）

这个式子是易读的，仍不理解可以看看后面例子怎么运用的。

证明我们放到最后面。

也能合起来写作

\[\sum_{\phi\in(\mathcal B^M/G)}w(\phi)=\dfrac 1{|G|}\sum_{g\in G}\prod_{k=1}^m\left(\sum_{\beta\in\mathcal B}w^k(\beta)\right)^{j_k(g)} \]

但是这个就很丑了。

然后有几个特殊情形如下：

特殊情形 1

如果取 \(w(\beta)=1\)，那么有 OI-wiki 上的 Pólya 定理形式（这是普通计数题里常用的形式）

\[|\mathcal B^M/G|=\dfrac1{|G|}\sum_{g\in G}|\mathcal B|^{c(g)},~~c(g)=\sum j_k(g) \]

\(c(g)\) 也可以理解为 \(g\) 的循环数量。

因为 \(w\equiv1\) 所以所有 \(x_i=|B|\)，合并同类项易证。

特殊情形 2

如果取 \(w(\beta)=z^{|\beta|}\)，有（这是在生成函数里易用的形式）

\[\sum_{\phi\in(\mathcal B^M/G)}z^{|\phi|}=Z(G;B(z),\dots,B(z^m)) \]

其中 \(B(z)\) 表示组合类 \(\mathcal B\) 的（计数序列的）OGF。

代入易证。

特殊情形 3

如果取 \(G=S_m\)，有

\[\sum_{i=0}^\infty\sum_{\phi\in(B^{M_i}/S_i)}w(\phi)=\exp\left(\sum_{i=0}^\infty\dfrac{\sum_{\beta\in\mathcal B}w^i(\beta)}i\right)=\exp\left(\sum_{i=0}^\infty\dfrac{x_i}i\right) \]

其中 \(M_i\) 说的是集合 \(\{1,\dots,i\}\)。

证明我们放到最后面。

例题讲解

P4980 【模板】Polya 定理

有 \(n\) 个点 \(n\) 条边的环，有 \(n\) 种颜色，给每个顶点染色，问有多少种本质不同的染色方案，答案对 \(10^9+7\) 取模。

本质不同定义为不能通过旋转与别的染色方案相同。

\(n\leq10^9\)，多组数据。

求的是特殊情形 1 的 \(|\mathcal B^M/G|\)。\(\mathcal B\) 是全部 \(n\) 种颜色，\(G\) 是所有 \(n\) 个循环移位。易知，对于循环移 \(i\) 位，\(g_i\) 能分解为 \(\gcd(i,n)\) 个长为 \(n/\gcd(i,n)\) 的循环。也即 \(c(g_i)=\gcd(n,i)\)。

代入特殊情形 1，有

\[|\mathcal B^M/G|=\dfrac1{|G|}\sum_{g\in G}|\mathcal B|^{c(g)}=\dfrac1n\sum_{g\in G}n^{\gcd(i,n)} \]

后面是简单的数论处理，直接略过。

P2561 [AHOI2002] 黑白瓷砖

描述起来有点麻烦，直接看题面。

很容易发现这个的行为等价于对称群 \(S_3\)，因为 \(S_3\) 里面的三个元素任意排列就对应三角形的旋转翻转组合共六种操作（好像 3b1b 那个视频里面有这个动画）。

虽然是六种置换，但是是 \(N=n(n+1)/2\) 个元素进行置换，所以环的数量不是简单的 1/2/3。

分类讨论如下：

• 恒等变换 \([1,2,3]\)，此时所有元素不动，\(c(g)=N\)。
• 旋转变换 \([2,3,1],[3,1,2]\)，此时除了在 \(n=3k+1\) 时会存在的中心点外，每三元组都会轮换位置，贡献一个三元环，共计 \(c(g)=\lceil N/3\rceil\)。
• 翻转变换 \([1,3,2],[3,2,1],[2,1,3]\)，此时除了中心点每三元组贡献一个一元环和一个二元环，共计 \(c(g)=\lceil2N/3\rceil\)

可能有人不知道那个三元组是啥。就是关于中心，旋转 \(120^\circ\) 和 \(240^\circ\) 对应到的两个位置，可以结合题图理解。在一个变换里一个三元组是一个亚基，所有三元组以相同模式变换。

于是有答案为 \(\dfrac16(2^N+2\cdot2^{\lceil N/3\rceil}+3\cdot2^{\lceil2N/3\rceil})\)

相信通过这两道题能对特殊情形 1 建立出一些理解。接下来我们关注情形 2，涉及一些生成函数相关内容。

关于欧拉变换 / Pólya Exp / MSET 构造

OGF 的欧拉 \(\mathcal E\) 变换，Pólya \(\text{Exp}\) 运算，组合类的 \(\text{MSET}\) 构造。它的其中两个定义式如下：

\[\boxed{\mathcal E(F)=\prod_{k=1}^\infty\dfrac1{(1-z^k)^{[z^k]F(z)}}} \]

\[\boxed{\text{MSET}(\mathcal F)=\prod_{\alpha\in\mathcal F}\dfrac1{1-z^{|\alpha|}}} \]

容易看出它们等价。很好理解这个式子说了什么：对于一个大小为 \(k\) 的组合对象，选择任意次，导出的 OGF 为 \(1/(1-z^k)\)，全部相乘即可得到上二式。组合意义是 \(\text{MSET}(\mathcal F)\) 里每一个元素是 \(\mathcal F\) 中若干（可不选）元素的无序组合，\([z^k]\mathcal E(F)\) 就是所有总大小为 \(k\) 的无序组合总数。

补充：这个是在 OGF（无标号）体系下的。在 EGF（有标号）体系下相同组合意义的运算为函数 \(\exp\)。可以想一想造成这样区别的原因是什么。

但是这个式子并不 practical。我们固然可以使用简单的代数技巧把它化简，但是这里是例题。所以考虑通过 Pólya 定理进行计算。

关注组合意义：枚举选择组合对象数量 \(s\)，\(\mathcal B=\mathcal F\)，所有位置等价 \(\Rightarrow G=S_m\)，同时有权重 \(w(\beta)=z^{|\beta|}\)（为什么是 \(z^{|\beta|}\) 可以参考前面有根树那个例子）。

然后我们会发现，该情况同时满足情形 2 和情形 3，经过简单的代入，有

\[\boxed{\mathcal E(F)=\exp\sum_{k=1}^\infty\dfrac{F(z^k)}k} \]

然后这里有个简单的应用：

无标号有根树计数

See you again。设全部无标号有根树组成的组合类是 \(\mathcal T\)，对应 OGF \(T(z)\)。注意到：根节点的每一个儿子都可以是 \(\mathcal T\) 中的任意元素，儿子数量任意且互相不可区分。于是直接有

\[T(z)=z\cdot\mathcal E(T) \]

其中多出来的那个 \(z\) 表示根节点自己。

另外多说一句，关于拿到这个方程之后怎么办的问题，其实是可以牛顿迭代的。 \(\mathcal E(F)\) 中的项 \(F(z^2),F(z^3),\dots\) 在牛顿迭代时都是可以看作常数的，原因是求到 \(\pmod{z^{2n}}\) 时后面的东西都已知了。注意看作常数不代表就是常数，它们跟 \(F(z)\) 是有关的，然后还为什么能看作常数可以观察我那篇牛顿迭代的博客，类比 \(z\) 为啥可以看作常数。但是那篇文章有些与主旨无关的理解错误我没修，注意自行判断。总之就是说

\[z\cdot\mathcal E(T)=z\exp(T+\sum_{k=2}^\infty\dfrac{F(z^k)}k)=\exp T\cdot\color{b1518c}{z\exp\sum_{k=2}^\infty\dfrac{F(z^k)}k} \]

其中那一坨标紫色的求导时直接看作为 \(c\)。然后就是方程 \(T-c\exp T=0\)，易于迭代了。

而另一个解法是分治 FFT。严谨且易懂，但是我不会。

LOJ6538 烷基计数

每个点儿子数量不超过 \(3\) 的无标号有根树计数。

设它对应的组合类叫 \(\mathcal R\)，OGF 为 \(R(z)\)。（相信学过化学的同学知道为什么时这个字母。）

如果根节点有 \(0,1,2,3\) 个儿子的烷基分别叫做 \(\mathcal R_{0,1,2,3}\)，易知有 \(R(z)=R_0(z)+\dots+R_3(z)\)。那么考虑分别求出这四段。易知：

\[R_0(z)=z \]

\[R_1(z)=zR(z) \]

\(R_2\)：此时这两个儿子可交换，对应 \(G=S_2\)，有

\[R_2(z)/z=Z(G;x_1,x_2)=1/2\cdot(x_1^2+x_2)=\dfrac {R^2(z)}2+\dfrac{R(z^2)}2 \]

\(R_3\)：此时这三个儿子可任意交换，对应 \(G=S_3\)，有

\[R_3(z)/z=1/6\cdot(x_1^3+3x_1x_2+2x_3)=\dfrac{R^3(z)}6+\dfrac{R(z)R(z^2)}2+\dfrac{R(z^3)}3 \]

然后四部分加起来的方程直接牛顿迭代 / 分治 FFT 就好了。

Burnside 引理

我们仍然定义 \(M,m,G,\mathcal B,w\) 如上文。

Burnside 是干什么的呢？注意 Pólya 只能处理所有染色方案是全集 \(\mathcal B^M\) 时的问题。那么如果染色方案只有其中一部分的时候应该如何呢？

我们设有染色方案集合 \(\Phi\subseteq\mathcal B^M\) 使得 \(\forall \phi\in\Phi,g\in G,\phi\circ g\in\Phi\)，即保证 \(\Phi\) 在 \(g\) 作用下封闭。一般的问题应该都是满足的，因为普通的限制都是关于颜色数量的。

然后有 Burnside 引理：

\[\boxed{\sum_{\phi\in\Phi/G}w(\phi)=\dfrac1{|G|}\sum_{g\in G}\sum_{\phi\in\Phi}[\phi\circ g=\phi]w(\phi)} \]

这个式子应该也很易懂。

注意这个式子只涉及 \(w(\phi)\)（而非 \(w(\beta)\)），可能会有只定义关于 \(\phi\) 的 \(w\) 函数的情况。但是这时候还是需要保证 \(\forall \phi_1\sim\phi_2,w(\phi_1)=w(\phi_2)\)。其中 \(\sim\) 表示等价。

证明我们放到最后面。

取 \(w\equiv1\) 有（这个是平时见到的版本）

\[|\Phi/G|=\dfrac1{|G|}\sum_{g\in G}\sum_{\phi\in\Phi}[\phi\circ g=\phi] \]

注意求和的顺序是可以交换的。

例题讲解

UVA 10601 Cubes

12 根给定颜色的木棍拼正方体，问本质不同正方体数量。

正方体的旋转方式有 24 种，你都知道么？

每个置换能拆成若干环，那么一个 \(\phi ~s.t.~ \phi\circ g=\phi\) 就只需要保证每个环里颜色一样。那么简单组合一下就好了。

未知来源题

给一个 \(\mathcal B\) 上的置换 \(p\)，对于 \(\Phi\) 与 \(G\) 求 \(G\) 下所有本质不同的好的染色方案的个数。称一个染色方案是好的当且仅当 \(p(\phi)\sim\phi\)。

定义 \(w(\phi)=[p(\phi)\sim\phi]\)。由上文，我们需要验证该定义的合法性：

对于 \(\phi_0\sim\phi_1\)，即 \(\exists f\in G,f(\phi_0)=\phi_1\)。 若 \(w(\phi_0)=1\)，则有 \(\exists g\in G,g(\phi_0)=p(\phi_0)\)。所以 \(p(\phi_1)={\color{red}p(f(\phi_0))=f(p(\phi_0))}=f(g(\phi_0))=(f\circ g)(\phi_0)\Rightarrow p(\phi_1)\sim \phi_0\sim\phi_1\Rightarrow w(\phi_1)=1\)。\(w(\phi_0)=0\) 时类似。

注意 \(p(f(\phi_0))=f(p(\phi_0))\) 是因为 \(f\) 作用于 \(\phi_0\) 的定义域 \(M\)，而 \(p\) 作用于 \(\phi_0\) 的值域 \(\mathcal B\)，所以可以交换。

问题是，\(w(\phi)\) 该怎么快速计算呢？我们把这个问题放到证明之后。

证明

上文共出现了三个“证明我们放到最后面”，让我们证明之。

Burnside 引理

\[\sum_{\phi\in\Phi/G}w(\phi)=\dfrac1{|G|}\sum_{g\in G}\sum_{\phi\in\Phi}[\phi\circ g=\phi]w(\phi) \]

\(w(\phi)\) 这个东西在不等价的 \(\phi\) 之间是没有关系的，这启发我们分别对每个等价类计算之。

设有一等价类 \(\Phi_0\) 与其中一个染色方案 \(\phi_0\)。称 \(\Phi_0\) 为 \(\phi_0\) 的轨道（orbit）。注意由 \(\Phi\) 的封闭性，\(\Phi_0\) 里实际包含了 \(\mathcal B^M\) 里全部的与 \(\phi_0\) 等价的染色方案。易知 \(\Phi_0\) 在 \(g\) 作用下也封闭，于是将 \(\Phi_0\) 应用 burnside 引理有

\[w(\phi_0)=\dfrac1{|G|}\sum_{g\in G}\sum_{\phi\in\Phi_0}[\phi\circ g=\phi]w(\phi) \]

右边的 \(w(\phi)\) 实则全部是 \(w(\phi_0)\)，化简得

\[|G|=\sum_{\phi\in\Phi_0}\sum_{g\in G}[\phi\circ g=\phi] \]

对于 \(\phi\)，称集合 \(G_\phi=\{g|\phi\circ g=\phi\}\) 为 \(\phi\) 的稳定集（stablizer）。就是那些作用在 \(\phi\) 上使 \(\phi\) 不变的 \(g\)。

即证上面这个：每个等价染色方案稳定集大小之和等于置换群大小。

我们先来感受一下：

设一个大小为 \(m=4k\) 的圆上旋转+翻转的置换群 \(G\)，则 \(|G|=2m\)。设有如下染色方案：

易知等价染色方案共 \(m/2\) 种（\(180^\circ\) 范围内任意旋转），而对于每一种染色方案，稳定集都有 不变 / 旋转 \(180^\circ\) / 沿橙色中垂线翻转 / 沿蓝色中垂线翻转 四种置换。然后 \(m/2 \times 4=2m\)。

而如果置换群只有旋转，\(|G|=m\)，等价染色方案数不变为 \(m/2\)，而每个染色方案的稳定集就只有 不变 和 旋转 \(180^\circ\) 两种了。还是有 \(m/2\times2=m\)。

对于 \(\phi_0\)，我们可以通过所有 \(g\in G\) 将它变成某个 \(\phi\in\Phi_0\)。设能使 \(\phi_0\) 置换为某个 \(\phi_1\) 的全部 \(g\in G\) 组成的集合称为 \(K(\phi_1)\)，取其中一个置换 \(k_1\in K(\phi_1)\)。

\(\forall k\in K(\phi_1)\)，由群的除法性质，有且仅有一个 \(g_k\) 使 \(k_1\circ g_k=k\)。

让我们看看这相当于干了什么：对于一个染色方案 \(\phi_1\)，给出 \(k_1\) 使 \(\phi_0\circ k_1=\phi_1\)，然后又枚举了所有 \(g_k\) 使 \(\phi_0\circ(k_1\circ g_k)=\phi_1\)。又由群运算的结合律，\(\phi_1=\phi_0\circ(k_1\circ g_k)=(\phi_0\circ k_1)\circ g_k=\phi_1\circ g_k\)。也就是说，\(g_k\) 枚举了 \(\phi_1\) 的整个稳定集。

这段不是很理解可以转一转上面那个环。

如果觉得一堆复合看起来很晕也可以写成函数嵌套来看。

同时，对于每个 \(\phi_1\)，\(|G_{\phi_1}|\) 就是所有的 \(g_k\) 数量就是所有 \(k\) 的数量，也就是 \(|K(\phi_1)|\)。又因为枚举每一个 \(g\) 都将 \(\phi_0\) 置换为某一个 \(\phi_1\)，这也就是说 \(\sum_{\phi_1\in\Phi_0}|K(\phi_1)|=|G|\)。也就是 \(\sum_{\phi_1\in\Phi_0}|G_{\phi_1}|=|G|\)。证毕。

还能发现的一点是，\(\Phi_0\) 中每一个 \(|G_{\phi_1}|\) 其实是相等的。因为我们可以通过作变换 \(k_1^{-1} \circ k_2\) 的方式将每一个 \(K(\phi_1)\) 中的置换变换为 \(K(\phi_2)\) 中的置换。这推出 \(|K(\phi_1)|\leq|K(\phi_2)|\)。同理通过变换 \(k_2^{-1}\circ k_2\) 有 \(|K(\phi_1)|\geq|K(\phi_2)|\)。于是 \(|K(\phi_1)|=|K(\phi_2)|\)，即 \(|G_{\phi_1}|=|G_{\phi_2}|\)。

再代入 \(\sum_{\phi_1\in\Phi_0}|G_{\phi_1}|=|G|\)，有轨道-稳定集定理（Orbit-stabilizer theorem）：\(\forall \Phi_0, |\Phi_0||G_{\phi_0}|=|G|\)。

Pólya 定理

\[\sum_{\phi\in(\mathcal B^M/G)}w(\phi)=\dfrac 1{|G|}\sum_{g\in G}\prod_{k=1}^m\left(\sum_{\beta\in\mathcal B}w^k(\beta)\right)^{j_k(g)} \]

很好理解。令 \(\Phi=\mathcal B^M\)，代入 Burnside 引理有

\[\sum_{\phi\in(\mathcal B^M/G)}w(\phi)=\dfrac1{|G|}\sum_{g\in G}\sum_{\phi\in\mathcal B^M}[\phi\circ g=\phi]w(\phi) \tag 1 \]

对于 \(g\) 中每一个环，需要使它们都只含一种颜色才能让 \(\phi\circ g=\phi\)。将 \(w(\phi)=\prod_{k\in M}w(\phi(k))\) 拆解为每个环上权值的乘积，而一个环的权值为其上所有颜色权值乘积。设一个环长度为 \(k\)，颜色为 \(\beta\in\mathcal B\)，那么它有权值 \(\prod_{i=1}^kw(\beta)=w^k(\beta)\)。将一个 \(\phi\) 对于 \(g\) 分解为（环长，颜色）二元组可重集 \(L\)，则 \(w(\phi)\) 为

\[\prod_{(k,\beta)\in L}w^k(\beta)=\prod_{k=1}^m\left(w^k(\beta)\right)^{j_k(g)} \]

每个环都能取遍全部颜色集合。于是对于一个 \(g\)：

\[\sum_{\phi\in\mathcal B^M}[\phi\circ g=\phi]w(\phi)=\prod_{k=1}^m\left(w^k(\beta_1)+w^k(\beta_2)+\dots\right)^{j_k(g)}=\prod_{k=1}^m\left(\sum_{\beta\in\mathcal B}w^k(\beta)\right)^{j_k(g)} \]

然后将这个等式代入式 \((1)\) 即证。

提供如下理解：

拆出每个环，上式

\[=\prod_{k\in L}(w^k\left(\beta_1)+w^k(\beta_2)+\dots\right) \]

也就是对于每个环，取其中一项 \(w^k(\beta_i)\) 乘起来，相当于就对全部环的染色方案枚举了。

Pólya 定理 · 特殊情形 3

\[\sum_{i=0}^\infty\dfrac1{i!}\sum_{g\in S_i}\prod_{k=1}^ix_k^{j_k(g)}=\exp\left(\sum_{i=0}^\infty\dfrac{x_i}i\right) \]

这个证明偏组合一点。

由长度为 \(\{l_1,l_2,\dots,l_t\}(\sum l=i)\) 的环构成的 \(g\) 共有

\[\binom i{l_1,l_2,\dots,l_t}\cdot\prod_k(l_k-1)! \]

个。这是因为：首先枚举每个环是哪些元素，然后环内部圆排列。

原式可改写为

\[=\sum_{i=0}^\infty\dfrac1{i!}\cdot\sum_{t,\{l_j\},\Sigma l=i}\binom i{l_1,l_2,\dots,l_t}\cdot\prod_k x_{l_k}^{l_k}(l_k-1)! \]

后面部分两个连乘合起来了。然后拆开多重集组合有

\[=\sum_{i=0}^\infty\sum_{t,\{l\},\Sigma l=i}\prod_k x_{l_k}^{l_k}/l_k \]

拆出来的分子和前面抵消了，分母和后面抵消了。

注意枚举无序多重集 \(\{l\}\) 相当于枚举序列 \(l\) 再乘 \(1/t!\)。注意枚举 \(i\) 其实无意义，分步得

\[=\sum_{i=0}^\infty\sum_{t,l_j,\Sigma l=i}\dfrac1{t!}\prod_k x_{l_k}^{l_k}/l_k= \sum_{t,l_j}\dfrac1{t!}\prod_k x_{l_k}^{l_k}/l_k \]

再考虑右式，展开 \(\exp\) 得

\[\sum_{t=0}^\infty\dfrac{(\sum_{l=0}^\infty x_l/l)^t}{t!} \]

再展开那个 \(t\) 次方，跟上面 Pólya 定理最后那步相似，枚举这 \(t\) 项里每一项的 \(l(l_k)\) 分别是谁，再乘起来。于是二式一样，证毕。

回音

回到之前那题。

由 Burnside 引理的证明，我们知道若 \(\phi_1\sim\phi_0\)，则恰有 \(|G_{\phi_0}|\) 个 \(g\in G\) 使 \(\phi_0\circ g=\phi_1\)。于是

\[w(\phi)=[\phi\sim p(\phi)]=[\exists g\in G,g(\phi)=p(\phi)]=\dfrac1{|G_{\phi}|}\sum_{g\in G}[g(\phi)=p(\phi)] \]

这样再套用 Burnside 引理，有

\[\begin{aligned} &\dfrac1{|G|}\sum_{g\in G}\sum_{\phi\in\Phi}[g(\phi)=\phi]w(\phi)\\ =&\dfrac1{|G|}\sum_{g\in G}\sum_{\phi\in\Phi}[g(\phi)=\phi]\dfrac1{|G_\phi|}\sum_{f\in G}[f(\phi)=p(\phi)]\\ =&\dfrac1{|G|}\sum_{\phi\in\Phi}\sum_{f\in G}[f(\phi)=p(\phi)]\dfrac1{|G_\phi|}\sum_{g\in G}[g(\phi)=\phi]\\ =&\dfrac1{|G|}\sum_{\phi\in\Phi}\sum_{f\in G}[f(\phi)=p(\phi)]\\ \end{aligned} \]

很神奇吧，因为还由于刚刚那句话，倒数第二步比最后一步多出来的那一坨是 \(1\)。然后就易于计算了。

后记

这篇文章 markdown 源码有 20K，（莫名其妙恰好）666 行。断断续续写了一周才写完。

那几个证明本来不打算写的，因为不知道怎么证的，但是后来在文化课上给整出来了，没有使用恼人的群论定义。十分高兴且骄傲。

后半部分对 \(f\circ g\) 和 \(g(f)\) 的混用导致不太易于阅读，Burnside 引理证明那块写的更是更是。

从第三个大标题开始，我假设了读者已经建立了对置换群的完整认知，所以对置换群内容没有详细描述。

更后面不是很 visualized 和 delicated 也是出于相同的原因。

有任何文章的问题可以提出。应当会有笔误的。

有任何看不懂的直接评论。

最后仍然需要感谢 @PWT 的大力支持。