洛谷题单指南-组合数学与计数-CF1332E Height All the Same

原题链接：https://www.luogu.com.cn/problem/CF1332E

题意解读：n*m二维矩阵中，每个位置有一个数字a_ij∈[L,R]，有两种操作：

1、将相邻两个数字各加1

2、将一个数字加2

问有多少种初始状态，使得通过以上操作将所有数变成相同。

解题思路：

1、问题分析

  最终要使得所有数相同，也就是同奇同偶，而操作2无法改变奇偶性，操作1可以改变奇偶性，因此只要通过操作1将所有数改成同奇同偶，

再通过操作2即可将数字变为相同。

2、条件约束

  什么状态通过操作1能改为同奇同偶呢？需要深入理解操作1的两个重要性质：

性质一：对一奇一偶两个数进行操作1，两数奇偶互换，在二维矩阵中起到了将一个奇数或者偶数移动的效果。

性质二：对两奇或两偶的数进行操作1，两数奇偶变化，起到了将数据往同一个奇偶性改变的效果。

因此，要通过操作1将所有数改为同奇同偶，初始状态中必须有偶数个奇数或者偶数。

如何理解？通过操作1可以将某种数（奇或偶）移动到矩阵的一侧，然后再通过操作1可以将所有一侧的数改变奇偶性，由于一次操作2个数，

必须要有偶数个同奇偶性的数才行。

3、分类讨论

设size=n*m，len = R - L + 1，矩阵中奇数个数为odd，偶数个数为even，size = odd + even

当size是奇数时，odd和even中必然有一个是偶数，因此这样的初始状态都是满足要求的，一共有len^size个；

当size时偶数时，odd和even必须都是偶数才行，两个都是奇数的情况则不行，这样的状态数量可以通过枚举odd累加：

  odd取0、2、4...size/2，L~R中奇数的个数为o，偶数的个数为e

  e = R/2 - (L+1)/2 + 1

  o = len - e

  总的数量为

4、公式推导

上面的式子很像二项式定理，我们知道根据二项式定理有

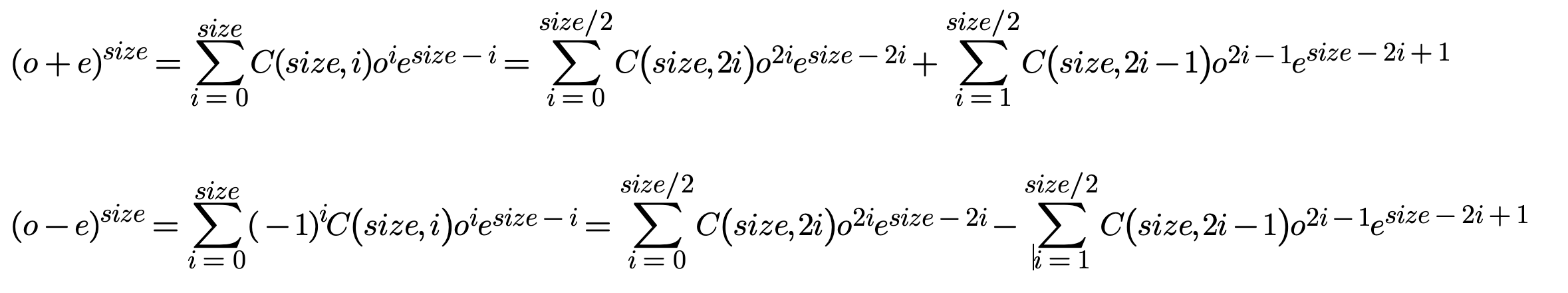
由以上两式相加可推导出：

5、算法求解

对于以上两种情况，通过快速幂和逆元求解。

100分代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;

const int MOD = 998244353;
LL n, m, L, R;

LL ksm(LL a, LL b, LL mod)
{
    LL res = 1;
    while(b)
    {
        if(b & 1) res = res * a % mod;
        a = a * a % mod;
        b >>= 1;
    }
    return res;
}

int main()
{
    cin >> n >> m >> L >> R;
    LL size = n * m, len = R - L + 1;
    LL o = R / 2 - (L + 1) / 2 + 1; //区间内偶数个数
    LL e = len - o; //区间内奇数个数
    LL ans = 0;
    if(size % 2 == 1) //总数为奇数
    {
        ans = ksm(len, size, MOD);
    }
    else //总数为偶数
    {
        ans = (ksm(o + e, size, MOD) + ksm(abs(o - e), size, MOD)) % MOD;
        ans *= ksm(2, MOD - 2, MOD); //除以2变成乘以2的逆元
        ans %= MOD;
    }
    cout << ans;
    return 0;
}