洛谷题单指南-图论之树-P3384 【模板】重链剖分/树链剖分
原题链接:https://www.luogu.com.cn/problem/P3384
题意解读:对树上某条最短路径(u到v的最短路径就是u-lca(u,v)-v)上的点修改(给每个点增加值)和查询(路径上所有点的和);对子树所有点修改(子树每个点增加值)和查询(子树所有点的和)。
解题思路:
暴力做法:路径修改和求和可以通过LCA得到路径,枚举路径上所有点即可;子树修改和求和也可以通过DFS枚举实现,每一次操作都是O(n),n次操作需要O(n^2)。
重链剖分:重链剖分,也叫树链剖分,是一种将树结构转化为线性结构的算法技巧,主要用于高效处理树上路径的修改和查询问题。通过将树剖分成若干条重链,能把树上路径问题转化为区间问题,进而借助线段树、树状数组等高效的数据结构来解决。
对于树上路径的修改和查询,可以将任意路径拆分成若干"重链",只要使得每条重链在DFS中是有序的,即可将重链转换为区间,进而将问题转换为区间修改和查询问题,可以借助线段树解决。
对于子树的修改和查询,只要子树所有节点在DFS中是有序的,即可将子树转换为区间,同样可以将问题转换为区间修改和查询问题,借助线段树解决。
下面介绍具体如何做,先介绍几个基本概念:
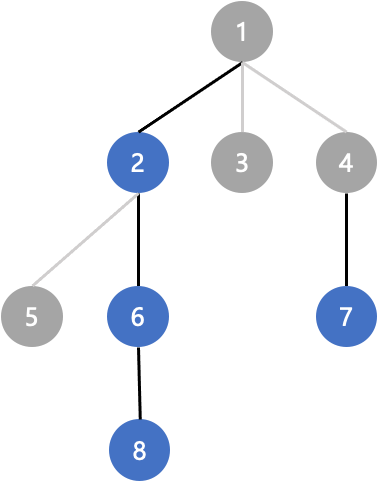
节点 1:子节点有 2、3、4。以 2 为根的子树节点数为 4(包含 2、5、6、8),以 3 为根的子树节点数为 1(只有 3),以 4 为根的子树节点数为 2(包含 4、7)。所以节点 1 的重儿子是 2,(1, 2) 是重边,(1, 3) 和 (1, 4) 是轻边。
节点 2:子节点有 5、6。以 5 为根的子树节点数为 1(包含 5),以 6 为根的子树节点数为 2(6、8)。所以节点 2 的重儿子是 6,(2, 6) 是重边,(2, 5) 是轻边。
节点 4:子节点有 7,所以节点 4 的重儿子是 7,(4, 7) 是重边。
重链 1:1 - 2 - 6 - 8
重链 2:5
重链 3:3
重链 4:4 - 7
下面看一下树中节点在搜索中的顺序:
DFS序:DFS 序(Depth-First Search Order)是对树或图进行深度优先搜索(DFS)时,记录节点被访问的先后顺序所得到的序列。
比如上图中,进行DFS节点遍历的顺序为:1 2 5 6 8 3 4 7,如果要修改和查询的路径是8到7,中间涉及节点1 2 6 8和4 7两条重链,但是1 2 6 8在DFS序中不是连续的,无法转换为序列区间问题。
如果在DFS的过程中,优先处理重儿子,那么这样进行DFS节点遍历的顺序变为:1 2 6 8 5 3 4 7,可以看出,1 2 6 8和4 7两条重链在此时的DFS序中是连续的,可以分别对这两个区间[1,4], [7,8]进行修改和查询即可,用线段树来维护DFS出来的序列即可。
问题的关键,就变成了如何标识出所有的重链,以及如何将一条路径剖分成多条重链,并且要证明任意路径剖分出的重链条数是足够少的,这样用线段树操作才不至于超时。
关键的性质证明
轻边性质: 从任意节点u到根节点的路径上,轻边的数量不超过logn条。
证明:对于轻边(u,v)(v是u的轻儿子),有sz(v)<sz(u)/2。因为如果sz(v)>=sz(u)/2,那么v就会是u的重儿子。每经过一条轻边,子树大小至少减半,而树的节点总数为n,所以从任意节点到根节点经过的轻边数量最多为logn条。
重链性质: 从任意节点u到根节点的路径上,重链的数量不超过logn条。
证明:重链的切换必然要经过一条轻边。设从节点u到根节点的路径上重链数量为k,重链切换次数为k-1,而重链切换次数等于轻边数量。由于轻边数量不超过logn条,所以k-1<=logn,即k<=logn+1,在复杂度分析中可认为重链数量不超过logn条。
接下来看重链剖分的实现步骤:
重点说明dfs2(v, v)这句的含义:
在 dfs2 函数里,dfs2(v, v) 这行代码用于处理节点 u 的轻儿子 v。下面详细分析其意义:
开启新的重链:当遇到轻儿子 v 时,意味着要开启一条新的重链。由于轻儿子 v 是这条新重链的起始节点,所以将 v 作为这条重链的顶端节点,也就是把 top[v] 设为 v。因此,调用 dfs2(v, v) 能确保 top[v] 被正确设置为 v,从而开启一条以 v 为顶端节点的新重链。
递归处理子树:调用 dfs2(v, v) 还会递归地处理以 v 为根的子树。在递归过程中,重链上的节点编号会依次递增,保证同一条重链上的节点编号连续。
下面详细描述如何将树上任意两点u和v之间的路径拆分为若干条重链:
步骤 1:确定两点所在重链的顶端节点
通过重链剖分的预处理,我们已经记录了每个节点所在重链的顶端节点 top[u] 和 top[v]。
步骤 2:比较顶端节点的深度
比较 top[u] 和 top[v] 的深度,选择深度较大的那个节点(假设为u)进行操作。
步骤 3:处理当前重链
将从u到 top[u] 这一段重链加入到路径拆分结果中。由于重链上的节点编号是连续的,我们可以将这一段重链看作一个区间,利用线段树等数据结构对该区间进行查询或修改操作。
步骤 4:跳到上一条重链
将u更新为 fa[top[u]],即跳到当前重链顶端节点的父节点,从而进入上一条重链。
步骤 5:重复步骤 2 - 4
不断重复上述步骤,直到 top[u] 和 top[v] 相同,此时u和v位于同一条重链上。
步骤 6:处理最后一条重链
当u和v位于同一条重链上时,将从u到v这一段重链加入到路径拆分结果中。
代码示例
// 树上路径剖分成重链
void getPath(int u, int v) {
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) swap(u, v);
// 从 u 到 top[u] 这一段重链的信息
// 对应dfs序列中的节点:dfn[top[u]] ~ dfn[u],对其进行线段树区间操作即可
u = fa[top[u]]; // 跳到上一条重链
}
if (dep[u] > dep[v]) swap(u, v);
// 从 u 到 v 这一段重链的信息
// 对应dfs序列中的节点:dfn[u] ~ dfn[v],对其进行线段树区间操作即可
}示例说明
假设有如下一棵树:
1
/ | \
2 3 4
/| |
5 6 7
/
8经过重链剖分后,重链有:
- 重链 1:1 - 2 - 5 - 8
- 重链 2:6
- 重链 3:3
- 重链 4:4 - 7
现在要查询节点 u=6 到节点 v=7 之间路径上的节点权值之和。
通过这种方式,我们将树上路径拆分为若干条重链,利用线段树对每条重链进行查询或修改操作,从而高效地解决树上路径问题。由于重链的数量不超过 条,每次操作线段树的时间复杂度为O(logn),所以总的时间复杂度为O(lognlogn),如果一共进行n次操作,复杂度为O(nlognlogn)。
应用场景:
详细解释:
updateSubtree 函数:由于子树内节点的编号是连续的,以节点 u 为根的子树节点编号范围是 [dfn[u], dfn[u] + sz[u] - 1],因此直接对该区间进行修改。
querySubtree 函数:同理,查询以节点 u 为根的子树节点编号范围 [dfn[u], dfn[u] + sz[u] - 1] 的区间和。
基于以上介绍,本题就是重链剖分的典型模版题,下面给出完整代码。
100分代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 100005;
vector<int> g[N]; //领接表
int a[N]; //节点上初始值
int sz[N]; //子树大小
int fa[N]; //父节点
int depth[N]; //深度
int son[N]; //重儿子
int dfn[N], cnt; //节点的dfs序号
int rk[N]; //dfs序号对应的节点
int top[N]; //节点所在重链的顶端节点
struct Node
{
int l, r; //节点的区间
LL sum, add; //sum是区间和,add是懒标记表示所有子节点要增加的值
} tr[N * 4]; //线段树
int n, m, r, p;
void addtag(int u, int tag)
{
tr[u].sum += (tr[u].r - tr[u].l + 1) * tag;
tr[u].sum %= p;
tr[u].add += tag;
tr[u].add %= p;
}
void pushup(int u)
{
tr[u].sum = (tr[u << 1].sum + tr[u << 1 | 1].sum) % p;
}
void pushdown(int u)
{
if(tr[u].add)
{
addtag(u << 1, tr[u].add);
addtag(u << 1 | 1, tr[u].add);
tr[u].add = 0;
}
}
void build(int u, int l, int r)
{
tr[u] = {l, r};
if(l == r) tr[u].sum = a[rk[l]];
else
{
int mid = l + r >> 1;
build(u << 1, l, mid);
build(u << 1 | 1, mid + 1, r);
pushup(u);
}
}
void update(int u, int l, int r, int val)
{
if(tr[u].l >= l && tr[u].r <= r) addtag(u, val);
else if(tr[u].l > r || tr[u].r < l) return;
else
{
pushdown(u);
update(u << 1, l, r, val);
update(u << 1 | 1, l, r, val);
pushup(u);
}
}
LL query(int u, int l, int r)
{
if(tr[u].l >= l && tr[u].r <= r) return tr[u].sum;
else if(tr[u].l > r || tr[u].r < l) return 0;
else
{
pushdown(u);
return (query(u << 1, l, r) + query(u << 1 | 1, l, r)) % p;
}
}
void dfs1(int u, int p, int d)
{
sz[u] = 1; //初始化子树大小
fa[u] = p; //更新父节点
depth[u] = d; //更新深度
for(auto v : g[u])
{
if(v == p) continue;
dfs1(v, u, d + 1);
sz[u] += sz[v]; //更新子树大小
if(sz[v] > sz[son[u]])
{
son[u] = v; //更新重儿子
}
}
}
void dfs2(int u, int t)
{
top[u] = t; //更新u所在重链的顶点
dfn[u] = ++cnt; //更新u的dfs序号
rk[cnt] = u; //更新序号cnt对应的节点
if(son[u]) dfs2(son[u], t); //优先遍历重儿子
for(auto v : g[u])
{
if(v == fa[u] || v == son[u]) continue;
dfs2(v, v); //轻儿子v一定是一条重链的顶点
}
}
void updatePath(int u, int v, int val)
{
while(top[u] != top[v]) //如果所在重链顶端不相等
{
if(depth[top[u]] < depth[top[v]]) swap(u, v); //使得u所在重链顶端深度更大
update(1, dfn[top[u]], dfn[u], val); //取top[u] ~ u之间的重链序列进行更新
u = fa[top[u]]; //u跳到所在重链顶端的父节点,也就是上一条重链末尾
}
if(depth[u] > depth[v]) swap(u, v); //使得u深度比v小
update(1, dfn[u], dfn[v], val); //取u ~ v之间的重链序列进行更新
}
int queryPath(int u, int v)
{
LL res = 0;
while(top[u] != top[v]) //如果所在重链顶端不相等
{
if(depth[top[u]] < depth[top[v]]) swap(u, v); //使得u所在重链顶端深度更大
res += query(1, dfn[top[u]], dfn[u]); //取top[u] ~ u之间的重链序列进行更新
u = fa[top[u]]; //u跳到所在重链顶端的父节点,也就是上一条重链末尾
}
if(depth[u] > depth[v]) swap(u, v); //使得u深度比v小
res += query(1, dfn[u], dfn[v]); //取u ~ v之间的重链序列进行更新
return res % p;
}
void updateSubtree(int u, int val)
{
//以u为根的子树dfs序的起始序号是dfn[u],结束序号是dfn[u] + sz[u] - 1
update(1, dfn[u], dfn[u] + sz[u] - 1, val);
}
int querySubtree(int u)
{
//以u为根的子树dfs序的起始序号是dfn[u],结束序号是dfn[u] + sz[u] - 1
return query(1, dfn[u], dfn[u] + sz[u] - 1) % p;
}
int main()
{
int op, x, y, z;
cin >> n >> m >> r >> p;
for(int i = 1; i <= n; i++) cin >> a[i];
for(int i = 1; i < n; i++)
{
cin >> x >> y;
g[x].push_back(y);
g[y].push_back(x);
}
dfs1(r, 0, 0);
dfs2(r, r);
build(1, 1, n);
while(m--)
{
cin >> op;
if(op == 1)
{
cin >> x >> y >> z;
updatePath(x, y, z);
}
else if(op == 2)
{
cin >> x >> y;
cout << queryPath(x, y) << endl;
}
else if(op == 3)
{
cin >> x >> z;
updateSubtree(x, z);
}
else
{
cin >> x;
cout << querySubtree(x) << endl;
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号