2025年 蓝桥杯省赛C++A组题解
一、寻找质数
题目大意:找出第 2025 个质数。
【题解】:\(\pi(x)\)~\(\frac{x}{lnx}\),当 x 取到 30000 时,\(\frac{x}{lnx} \ge 2025\),用 欧拉筛 或者 埃氏筛\(O(n)\)算一下即可。
code:
#include <iostream>
using namespace std;
const int N = 3e5 + 10;
bool st[N];
bool is_prime[N];
typedef long long LL;
void f()
{
for(int i = 2; i < N; i+ )
{
if(!st[i])
{
is_prime[i] = true;
for(LL j = (LL)i * i; j < N; j + = i)
st[j] = true;
}
}
}
int main()
{
f();
int cnt = 2025;
for(int i = 1; i < N; i+ )
{
if(is_prime[i])
{
cnt--;
if(cnt == 0)
{
cout << i << endl;
break;
}
}
}
return 0;
}
二、黑白棋
题目大意:6 * 6 的棋盘,每个位置填黑白棋,填满的棋盘需要满足以下条件:
- 黑白棋子数量均等:
在每一行和每一列中,黑色棋子和白色棋子的数量必须相等。 - 相邻棋子限制:
在棋盘的任何一行或一列中,不能有超过两个相同颜色的棋子连续排列(即不允许出现“黑黑黑”或“白白白”的情况)。 - 行列唯一性:
每一行的棋子排列方式必须是唯一的,不能与棋盘中的任何其他行完全相同。
每一列的棋子排列方式必须是唯一的,不能与棋盘中的任何其他列完全相同。
行与列之间的棋子排列不作比较,即行可以与列相同,无需满足行列间的唯一性。
现在已经给定了初始的棋局状态,按照以上规定填满棋盘,答案唯一。
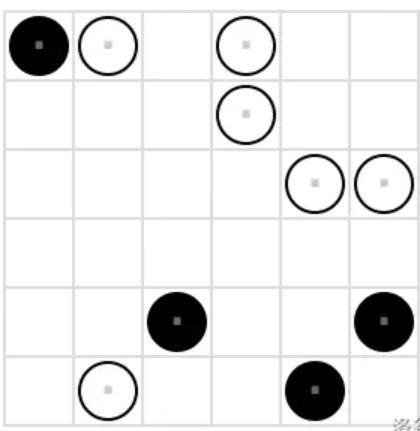
【题解】:暴力搜索
枚举每一行的状态,一共枚举 6 行,共有\(2^{36}\)种棋局,但因为初始给定的棋局可以剪枝、枚举每一行的过程中,行需要满足的相关性质可以剪枝,实际经过剪枝完成后到达最后去检查列相关性质的仅有 1296 种,暴力搜索时间完全够用,暴搜的具体细节看代码。
code:
#include <iostream>
#include <vector>
using namespace std;
const int N = 10;
int cnt = 0;
// 黑 -> 1, 白 -> 0, 2 -> 未知
int a[N][N] =
{
{1, 0, 2, 0, 2, 2},
{2, 2, 2, 0, 2, 2},
{2, 2, 2, 2, 0, 0},
{2, 2, 2, 2, 2, 2},
{2, 2, 1, 2, 2, 1},
{2, 0, 2, 2, 1, 2}
};
vector<vector<int>> path;
bool vis[N * N];
void dfs(int pos)
{
if(pos >= 6)
{
// cnt+ ;
// 1.列唯一性检查
for(int i = 0; i < 6; i+ )
{
for(int j = i + 1; j < 6; j+ )
{
bool flag = true;
for(int k = 0; k < 6; k+ )
{
if(path[k][i] != path[k][j])
{
flag = false;
break;
}
}
// 出现两列相同
if(flag) return;
}
}
// 2. 列相邻限制检查
for(int j = 0; j < 6; j+ )
{
for(int i = 0; i < 6; i+ )
{
int cnt = 0;
int k = i;
while(k < 6 && path[k][j] == path[i][j])
{
cnt+ ;
k+ ;
}
if(cnt > 2) return;
i = k - 1;
}
}
// 3. 列数量相同检查
for(int j = 0; j < 6; j+ )
{
int cnt0 = 0, cnt1 = 0;
for(int i = 0; i < 6; i+ )
{
if(path[i][j] == 0) cnt0+ ;
else cnt1+ ;
}
if(cnt0 != cnt1) return;
}
// 答案合法
for(auto& x : path)
for(auto& y : x)
cout << y;
// exit(0); // 答案唯一,其实也不需要退出,只会有一个合法答案
}
for(int st = 0; st < (1 << 6); st+ )
{
// 1.检查该列是否满足初始格子限制
vector<int> cur(6, 0);
for(int j = 0; j < 6; j+ ) cur[j] = (st >> j) & 1;
bool flag = true;
for(int j = 0; j < 6; j+ )
{
if(a[pos][j] == 2) continue; // 2 随便填
if(a[pos][j] != cur[j])
{
flag = false;
break;
}
}
if(!flag) continue;
// 2. 行数量相同检查
int cnt0 = 0, cnt1 = 0;
for(int j = 0; j < 6; j+ )
{
if(cur[j] == 0) cnt0+ ;
else cnt1+ ;
}
if(cnt0 != cnt1) continue;
// 3.行唯一性检查
int val = 0;
for(int j = 0; j < 6; j+ ) val |= (cur[j] << (5 - j));
if(vis[val]) continue;
// 4.相邻限制检查
flag = true;
for(int j = 0; j < 6; j+ )
{
int cnt = 0;
int k = j;
while(k < 6 && cur[k] == cur[j])
{
cnt+ ;
k+ ;
}
if(cnt > 2)
{
flag = false;
break;
}
j = k - 1;
}
if(!flag) continue;
// 5.合法,继续下一行
vis[val] = true;
path.push_back(cur);
dfs(pos + 1);
vis[val] = false;
path.pop_back();
}
}
int main()
{
dfs(0);
// cout << endl << cnt << endl;
return 0;
}
【题解】:推理
当个推理小游戏玩了,下面的推理流程种\((i, j)\)代表填入位置的行号和列号。
- \((1, 3)\)位置填白棋会违反相邻棋子限制,因此该位置填黑棋。
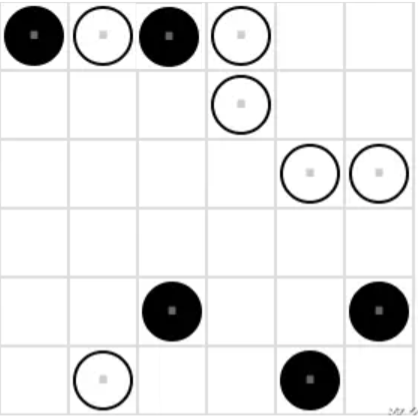
- \((3, 4)\)位置填白棋会违反相邻棋子限制,因此该位置填黑棋。
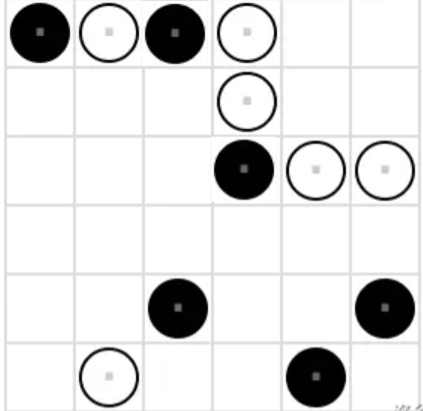
- \((3, 1)\)位置如果填白棋,3 行剩下位置只能填黑棋,违反相邻棋子限制,因此该位置填黑棋。
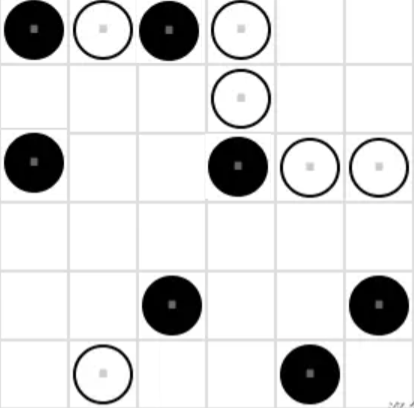
- \((2, 1)\)位置填黑棋违反相邻棋子限制,因此该位置填白棋。
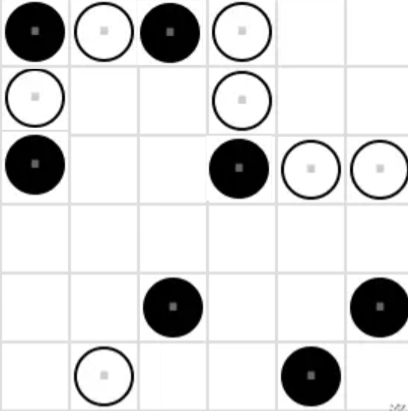
- \((6, 4)\)位置填白棋,4 列其余位置只能填黑棋,违反相邻棋子限制,因此该位置填黑棋。
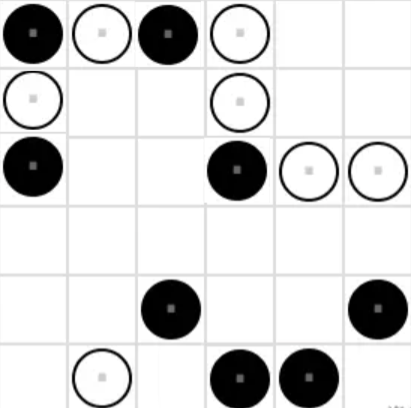
- \((6, 3)\)和\((6, 6)\)位置填黑棋会违反相邻棋子限制,因此填白棋。根据行列棋子数相同,6 行可以填完。
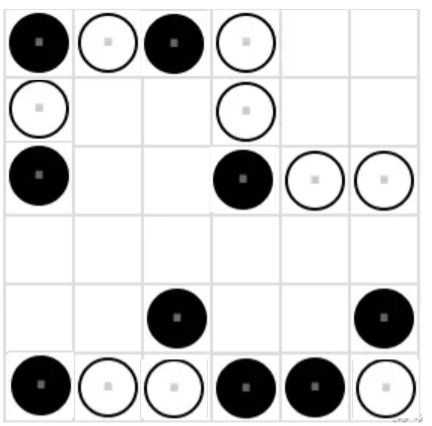
- 根据行列棋子数相同,1 列可以填完。
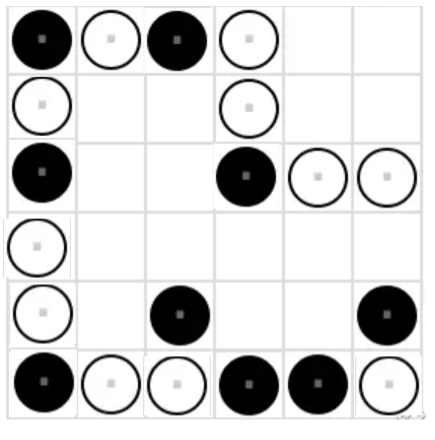
- \((5, 2)\)和\((2, 2)\)位置填白棋,2 列剩余位置只能填黑棋,违反相邻棋子限制,因此该位置只能填黑棋。

- 剩余位置同理,棋盘本身不大,直接填要不去暴搜简单不少。

三、抽奖
题目大意:3 个转盘,每个转盘上面有 n 个数,三个转盘转动,得到三个数字,满足以下条件的对应的分数。
- 三个相同的图案,积分 + 200;
- 两个相同的图案,积分 + 100;
- 三个数字图案,从左到右连续(例如 1,2,3),积分 + 200;
- 三个数字图案,经过顺序调整后连续(例如 2,1,3 或 3,2,1),积分 + 100;
抽奖机处于初始状态,三个转轮都处于第一个位置。每次开始抽奖,都会产生三个对应的随机数 xi1,xi2,xi3,表示第 j 个转轮会向后转动 xij 次停下。下次抽奖时,转轮会从上一次转动后的位置开始继续转动。
问 m 次执行后的分数。
【题解】:模拟
这个真没什么好说的,直接模拟吧。
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 1e3 + 10;
int n;
int a[N], b[N], c[N];
int m; int x, y, z;
bool check(vector<int>& val)
{
if(val[0] + 1 == val[1] && val[1] + 1 == val[2]) return true;
return false;
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i+ ) cin >> a[i];
for(int i = 1; i <= n; i+ ) cin >> b[i];
for(int i = 1; i <= n; i+ ) cin >> c[i];
int pos1 = 1, pos2 = 1, pos3 = 1;
cin >> m;
int ans = 0;
while(m--)
{
cin >> x >> y >> z;
pos1 = (pos1 + x) % n;
pos2 = (pos2 + y) % n;
pos3 = (pos3 + z) % n;
if(pos1 == 0) pos1 = n;
if(pos2 == 0) pos2 = n;
if(pos3 == 0) pos3 = n;
// cout << a[pos1] << " " << b[pos2] << " " << c[pos3] << endl;
int X = a[pos1], Y = b[pos2], Z = c[pos3];
if(X == Y && Y == Z) ans + = 200;
else if(X == Y || Y == Z || Z == X) ans + = 100;
vector<int> val = {X, Y, Z};
if(check(val))
{
ans + = 200;
continue;
}
sort(val.begin(), val.end());
if(check(val)) ans + = 100;
}
cout << ans << endl;
return 0;
}
四、红黑树
题目大意:根据下列规则构建满二叉红黑树。
- 根结点是一个红色结点;
- 如果当前结点 curNode 是红色结点,那么左子结点 curNode.left 是红色结点,右子结点 curNode.right 是黑色结点;
- 如果当前结点 curNode 是黑色结点,那么左子结点 curNode.left 是黑色结点,右子结点 curNode.right 是红色结点;
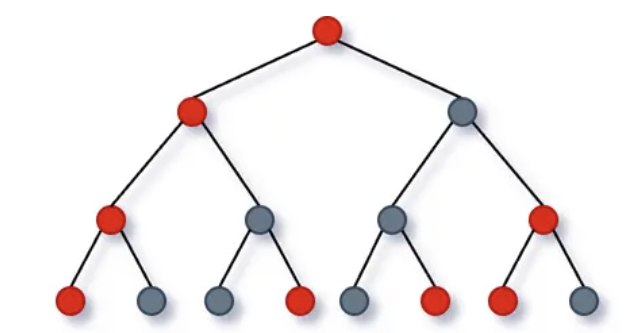
m次询问,对于每次询问回答结点颜色。
【题解】:模拟
n 最多会到 30 层,共\(2^{30}-1\)结点,预处理构建即可。
code:
#include <iostream>
#include <vector>
using namespace std;
const int N = 30;
vector<vector<int>> res;
int m;
// 红 -> 1, 黑 -> 0
void dfs(int pos)
{
if(pos > N) return;
vector<int> cur;
for(int i = 0; i < res[pos - 1].size(); i+ )
{
if(res[pos - 1][i] == 1)
{
cur.push_back(1);
cur.push_back(0);
}
else
{
cur.push_back(0);
cur.push_back(1);
}
}
res.push_back(cur);
}
int main()
{
cin >> m;
res.push_back(vector<int>{0});
res.push_back({1});
dfs(2);
while(m--)
{
int n, k;
cin >> n >> k;
cout << (res[n][k - 1] == 1 ? "RED" : "BLACK") << endl;
}
return 0;
}
五、黑客
题目大意:输入一个整数代表 n * m + 2 的值,后给出 n * m + 2 个数,你需要从中找出两个数 n 和 m 代表矩阵的行和列,剩余的数随便填,构成一个矩阵, 问不同矩阵的总个数。
【题解】:组合数学 数论
ps:做到这里有点怀疑 25 年的A,B 组是不是出反了,前面四道题个人感觉都没1200,这一题虽然洛谷给了绿色难度,但我感觉来也就1400的样子。
选定 n,m 之后,假定 x 这个数出现的次数为 mp[x](注意这里是除掉 n 和 m 之后的数的出现次数),剩余的数为 t 个,因为矩阵的行列都已经确定,所以可以把矩阵每行拉出来放一起组成一个以为的数组,总的填法显然是 t 的全排列,因为 t 中可能存在相同的数,所以 t 的全排列要除掉所有 x 的 mp[x] 的全排列之积。
倘若 n 和 m 不相同,那么矩阵转置之后必然不相等,此时 n,m 由上述算法算出来的答案需要乘 2。
反之 n 和 m 相同,矩阵转置后,数填的位置也必然是 t 的一种全排列,包含在上述算法的解中,因此不需要乘 2。
下面来明确一下代码的细节:
- \(fac[i]\):i 的阶乘。
- \(inv[i]\):i 的阶乘的逆元。
- \(s\_inv = \pi({mp[x]}!)\)这里的 mp[x] 并没有去除 n,m。
- 选定 n,m 之后,将\(s\_inv\)除掉 mp[n],mp[m],即乘两者的逆元。(如果 n = m,需乘 mp[n],mp[n] - 1 的逆元)。
code:
#include <iostream>
#include <unordered_map>
#include <cmath>
using namespace std;
typedef long long LL;
const LL MOD = 1e9 + 7;
const int N = 5e5 + 10;
LL fac[N], inv[N];
int n, a[N];
unordered_map<int, int> mp;
LL qpow(LL a, LL b)
{
LL res = 1;
while(b)
{
if(b & 1) res = res * a % MOD;
a = a * a % MOD;
b >>= 1;
}
return res;
}
void init()
{
fac[0] = 1;
for(int i = 1; i < N; i+ ) fac[i] = fac[i - 1] * i % MOD;
inv[N - 1] = qpow(fac[N - 1], MOD - 2);
for(int i = N - 2; i >= 0; i--) inv[i] = inv[i + 1] * (i + 1) % MOD;
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i+ )
{
cin >> a[i];
mp[a[i]]+ ;
}
init();
LL ans = 0;
int t = n - 2;
LL s_inv = 1;
for(auto& [x, y] : mp) s_inv = s_inv * fac[y] % MOD;
for(int x = 1; x <= sqrt(t); x+ )
{
if(!mp.count(x)) continue;
if(t % x != 0) continue;
if(!mp.count(t / x)) continue;
int y = t / x;
LL tmp1 = fac[t];
// tmp1 / tmp2
if(x != y)
{
LL tmp2 = s_inv * qpow(mp[x], MOD - 2) % MOD * qpow(mp[y], MOD - 2) % MOD;
LL tmp = tmp1 * qpow(tmp2, MOD - 2) % MOD * 2 % MOD;
ans = (ans + tmp) % MOD;
}
else
{
LL tmp2 = s_inv * qpow(mp[x], MOD - 2) % MOD * qpow(mp[x] - 1, MOD - 2) % MOD;
LL tmp = tmp1 * qpow(tmp2, MOD - 2) % MOD;
ans = (ans + tmp) % MOD;
}
}
cout << ans << endl;
return 0;
}
六、好串的数目
题目大意:给定一个数字字符串,求它的子串中满足下列条件之一的数目:
- 子串长度为 1。
- 长度为 1 且可以拆分成两个连续非递减子串。
【题解】:组合数学
- 连续非递减子串的所有子串一定满足条件。
- 两个相邻不同组的连续非递减子串通过组合也一定满足条件。
- 可以证明,满足条件的类别仅有上述两种。
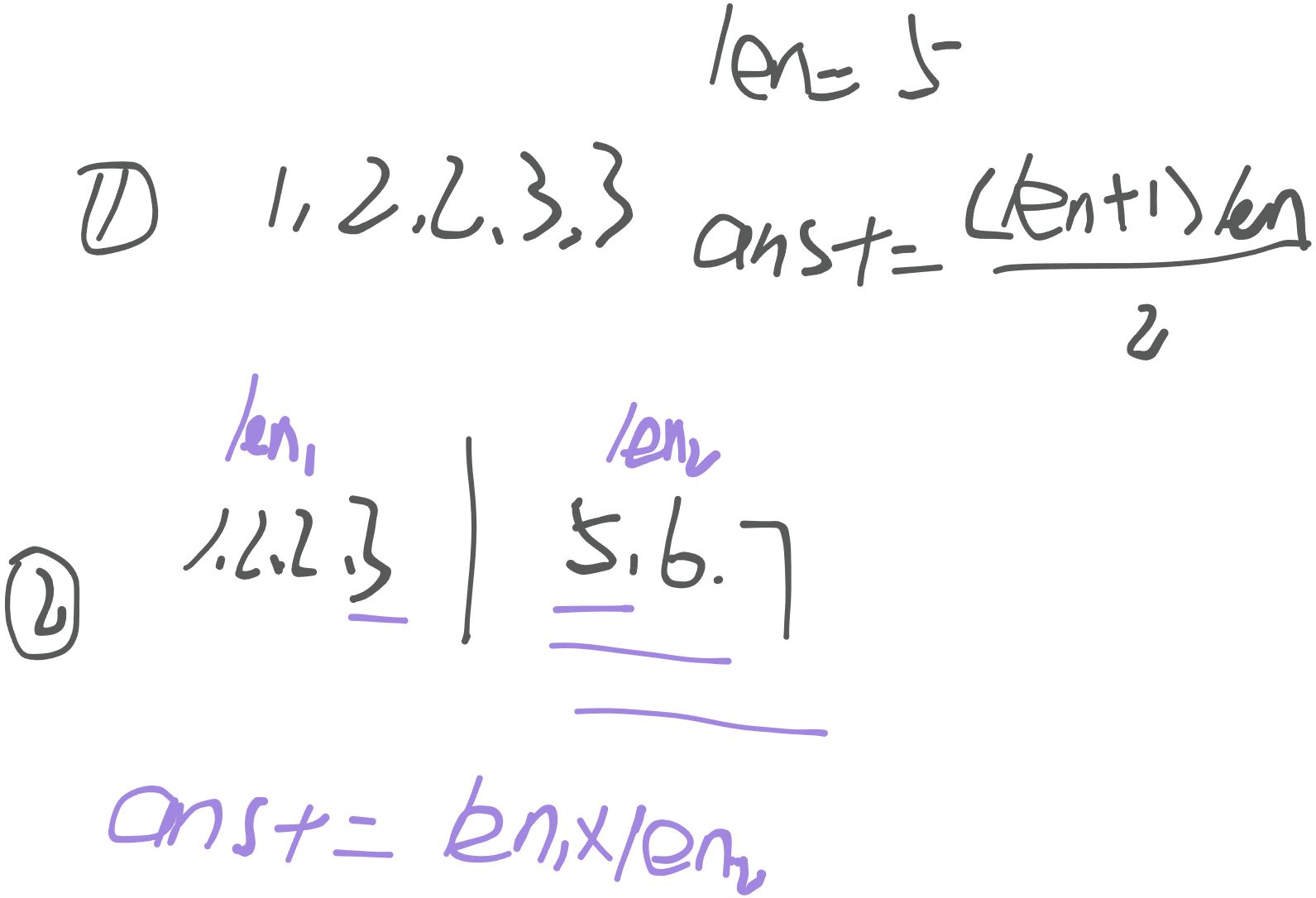
code:
#include <iostream>
#include <vector>
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 1e5 + 10;
string s;
int n;
int main()
{
cin >> s;
n = s.size();
s = " " + s;
vector<PII> t;
for(int l = 1; l <= n; l+ )
{
int r = l + 1;
while(r <= n && s[r] == s[r - 1] || s[r] - 1 == s[r - 1]) r+ ;
t.push_back({l, r - 1});
l = r - 1;
}
if(t.size() == 1)
{
cout << (LL)n * (n + 1) / 2 << endl;
return 0;
}
LL ans = 0;
for(int i = 0; i < t.size() - 1; i+ )
{
int l1 = t[i].first, r1 = t[i].second;
int l2 = t[i + 1].first, r2 = t[i + 1].second;
LL len1 = r1 - l1 + 1, len2 = r2 - l2 + 1;
ans + = len1 * len2;
}
for(int i = 0; i < t.size(); i+ )
{
int l = t[i].first, r = t[i].second;
LL len = r - l + 1;
ans + = len * (len + 1) / 2;
}
cout << ans << endl;
return 0;
}
七、地雷阵
题目大意:第一象限中埋有 n 颗地雷,第 i 颗地雷的坐标为$ (x_i,y_i)\(,触发范围为以\) (x_i,y_i)\(为圆心,半径为\)r_i$的圆。一旦小蓝走进圆内,就会触发地雷导致游戏失败。
求在\([0,\frac{\pi}{2}]\)中随机选择一个角度,通关游戏的概率。
【题解】:计算几何
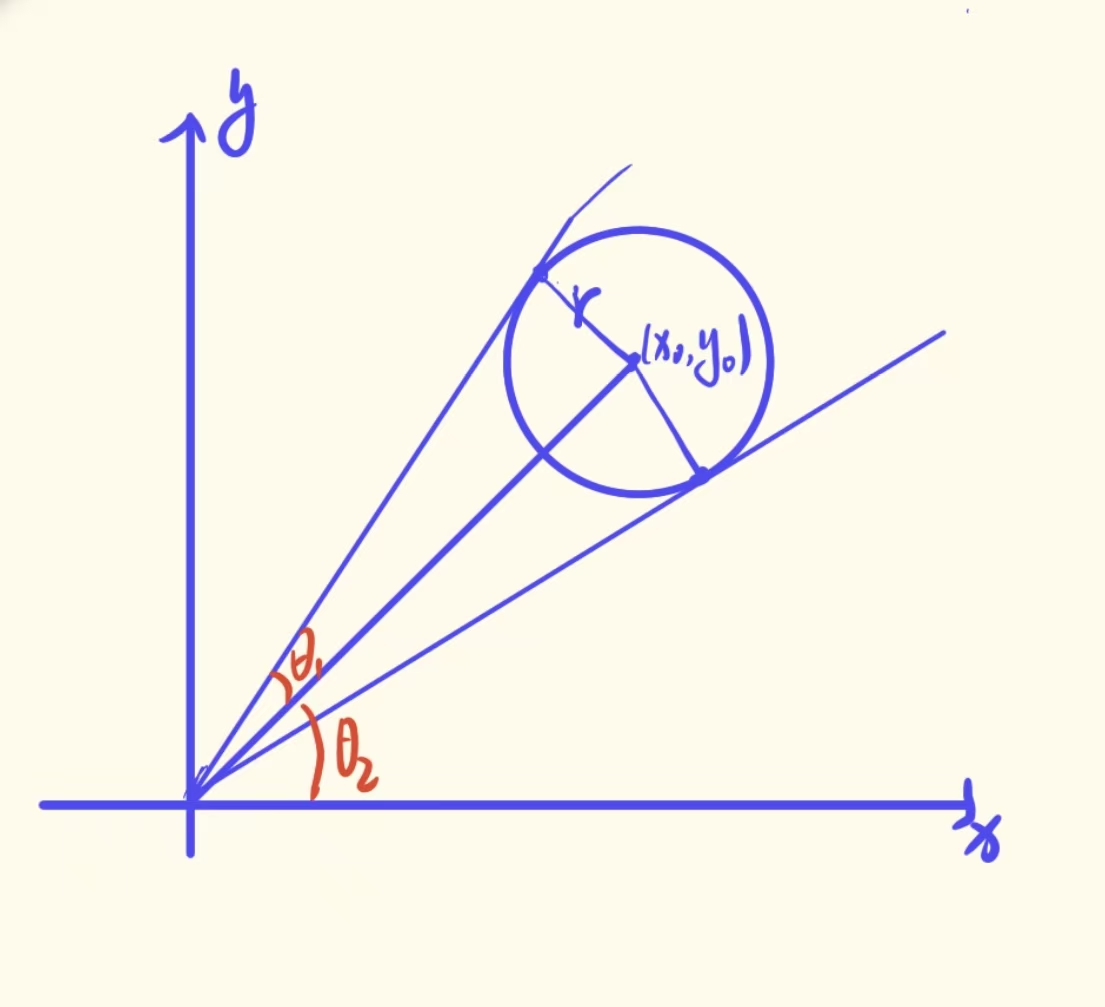
- 一个地雷与从原来的射线的范围为\([\theta_2-\theta_1, \theta_2+ \theta_1]\)。
- \(\sin\theta_1 = \frac{r}{\sqrt{x_0^2+ y_0^2)}}\)。
- \(\tan\theta_2=\frac{y_0}{x_0}\)。
计算出每个地雷的覆盖角度之后,区间合并求出最终覆盖角度,合并逻辑如下:
- 按照区间左端点排序。
- 新来区间的左端点小于等于前面区间的右端点,更新右端点为两者最大值。
- 新来区间的左端点大于前面区间的右端点,新开一段区间,把前面区间范围减掉。
code:
#include <iostream>
#include <cmath>
#include <vector>
#include <algorithm>
using namespace std;
typedef pair<double, double> PDD;
const double PI = 3.14159265358979323846;
const int N = 1e5 + 10;
int n;
double x[N], y[N], r[N];
vector<PDD> edges;
int main()
{
cin >> n;
for(int i = 1; i <= n; i+ ) cin >> x[i] >> y[i] >> r[i];
for(int i = 1; i <= n; i+ )
{
double theta_1 = asin(r[i] / sqrt(x[i] * x[i] + y[i] * y[i]));
double theta_2 = atan(y[i] / x[i]);
double start = theta_2 - theta_1;
double end = theta_2 + theta_1;
edges.push_back({start, end});
}
double rge = PI / 2;
sort(edges.begin(), edges.end());
double l = 0, r = 0;
for(int i = 0; i < edges.size(); i+ )
{
if(edges[i].first > r)
{
rge -= r - l;
l = edges[i].first;
r = edges[i].second;
}
else
{
r = max(r, edges[i].second);
}
}
rge -= r - l;
printf("%.3f\n", rge * 2 / PI);
return 0;
}
八、扫地机器人
题目大意:在一个含有 n 个点 n 条边的无重边无自环的连通无向图中,有一个扫地机器人在执行清扫作业。其中结点 i 的标记 ti∈{0,1}:如果为 1,则说明该结点需要进行清扫,扫地机器人在到达这个结点时会顺便进行清扫工作。机器人想知道,如果选定任意结点出发,每条边只能经过一次的话,最多能清扫多少个待清扫结点?
【题解】:基环树 拓扑排序 树形dp 树的直径 单调队列。
树是一个极小连通子图,在树的基础上连接任意两个节点,会形成一个环,这个结构就是基环树。
题中所说的 n 各节点 n 条边无重边无自环的无向连通图即为基环树。
对于基环树问题一般的思想是先分类讨论解的情况,讨论的思路为解在树中和解在环中或者两者的组合。
分类讨论:
选择一条无重边路径,求这条路径中节点权值为 1 的个数最大值。这很像树的直径问题。
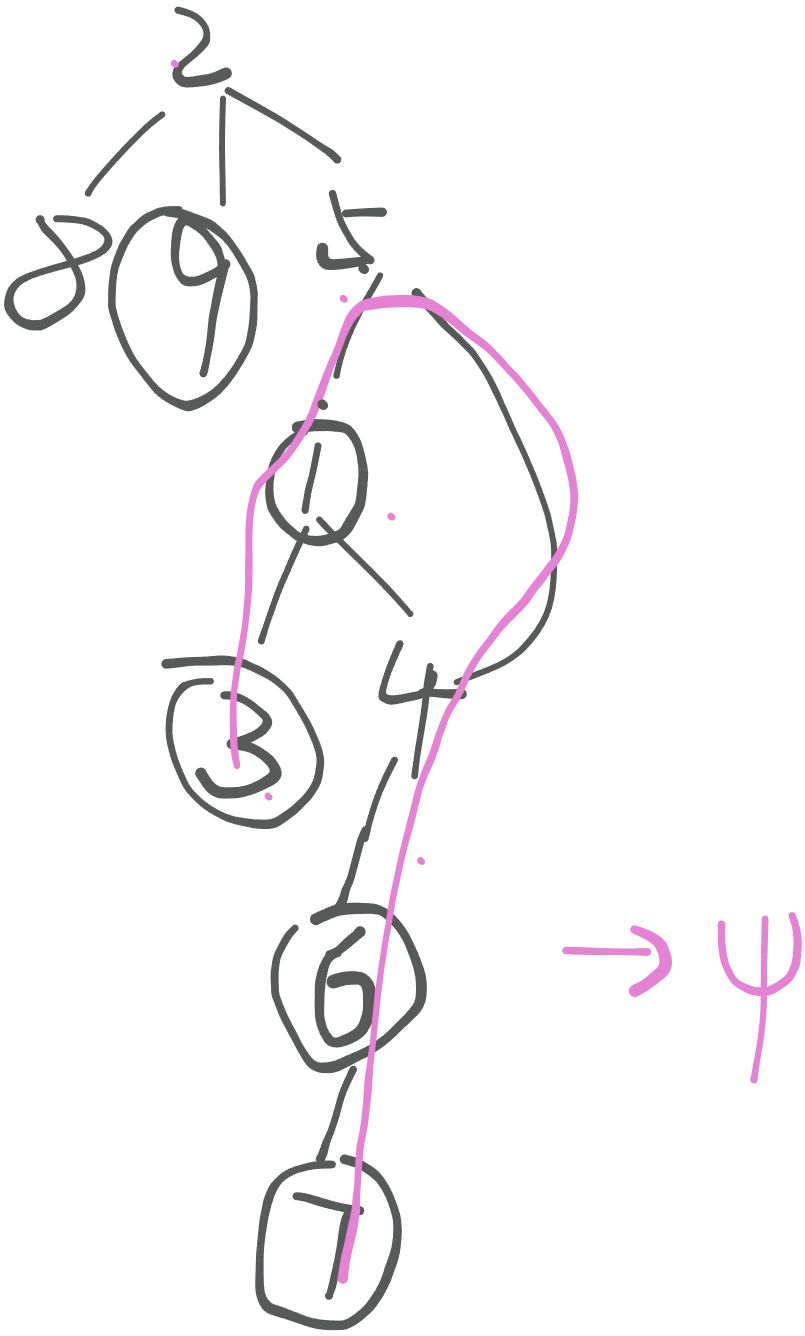
若这个问题单纯在树上,仅仅用树形dp很容易解决这个问题,而基环树对比于树多了一个环,从基环树中的节点往外延伸仅可能为一颗颗树(假设环中有 m 个节点,将环缩成一个点,边减少 m 条,剩余 n - m + 1个节点,n-m条边),因此答案如果仅在树上,和环压根就没有关系,但如果最终答案的路径经过环,必定会从环中节点延伸出去的树中选择两条延伸出去最长的路径(如果答案仅在环中,选择环外两条路径必定不劣),这个路径可能位于同一颗树
- 在做所有的工作之前,找到环是必要的,一般的拓扑排序找的是有向图中的环,所以初始入队列的是入读为 0 的节点,这里是无向图,存的双向边,可以从每个环延伸出去的树的叶结点做拓扑,这样入队列的就是度为 1 的节点,重复把度为 1 的节点入队列即可找到环。
void top_sort()
{
queue<int> q;
for(int i = 1; i <= n; i+ )
{
if(cnt[i] == 1) q.push(i);
}
while(!q.empty())
{
int t = q.front(); q.pop();
st[t] = true;
for(auto& x : edges[t])
{
cnt[x]--;
if(cnt[x] == 1) q.push(x);
}
}
}
- 答案位于仅在树中,不经过环(不考虑环中的节点)。
此时算答案就变成了单纯的树形dp求树的直径:
- 状态表示\(dp_x\):表示从 x 节点到叶结点的最长链。
- 状态转移:\(dp_x=min(dp_y)+ t_x\),y 为 x 的子节点,\(t_x\)为 x 节点的权值。
- 遍历顺序:dfs。
- 初始化:全部为 0 即可。
- 答案:\(dp_x\)为最长链,令该树的最长路径为 tmp,tmp 仅需在用子节点更新每个父节点的 dp 值的同时对所有的\(dp_x + dp_y\)取最大值,因为经过该节点的最长路径可以拆分为节点 x + 一条最长链 + 一条次长链,这么做的本质是在让\(dp_y\)去模拟其中一条链,前面已经算出来的\(dp_x\)模拟另一条链,若\(dp_y\)模拟的是最长链,次长链可能存在与于后面节点,当遍历到后面次长链的时候\(dp_y\)这个最长链将会存在于当前的\(dp_x\)中,更新答案正确,\(dp_x\)模拟的是次长链也是同理。
int dfs(int x, int fa)
{
int tmp = 0;
for(auto& y : edges[x])
{
if(y == fa || !st[y]) continue;
dfs(y, x);
// 更新 dp[x]
dp[x] = max(dp[x], dp[y]);
// 更新 tmp
tmp = max(tmp, dp[y] + dp[x]);
// 更新情况一的 ans
ans = max(ans, tmp + t[x]);
}
dp[x] + = t[x];
return ans;
}
- 答案经过环,延伸出来的两条链位于同一颗树中。
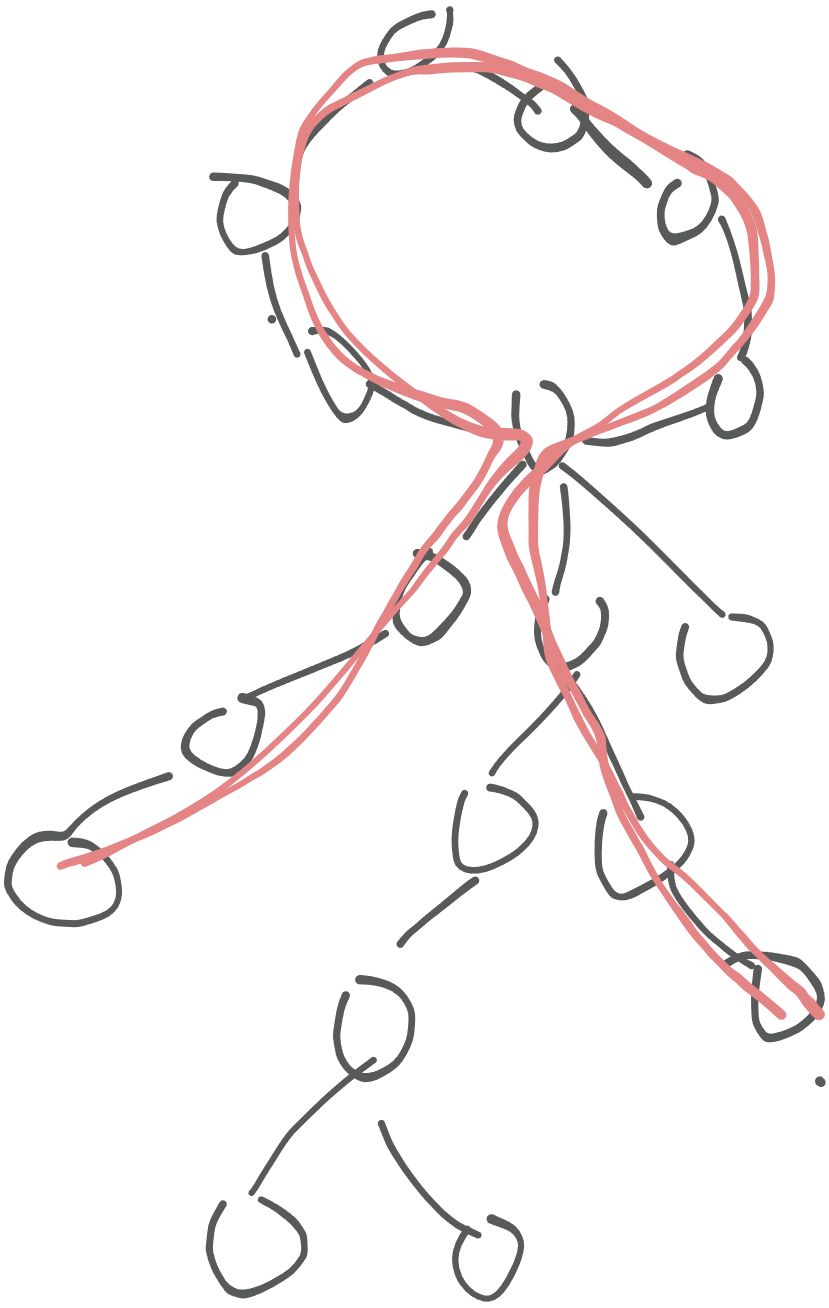
这两条位于同一颗树中的两条链,为以根节点的子节点中的最长的链和次长的链,即两个最大的 dp 值再加上环的长度,这一中情况的答案的第一部分即为上面求的根节点的 tmp 向上返回即可。
if(!st[i])
{
int tmp = dfs(i, 0);
// 答案的第二种情况
ans = max(ans, tmp + len);
}
- 答案经过环,延申的两条链位于不同的树中
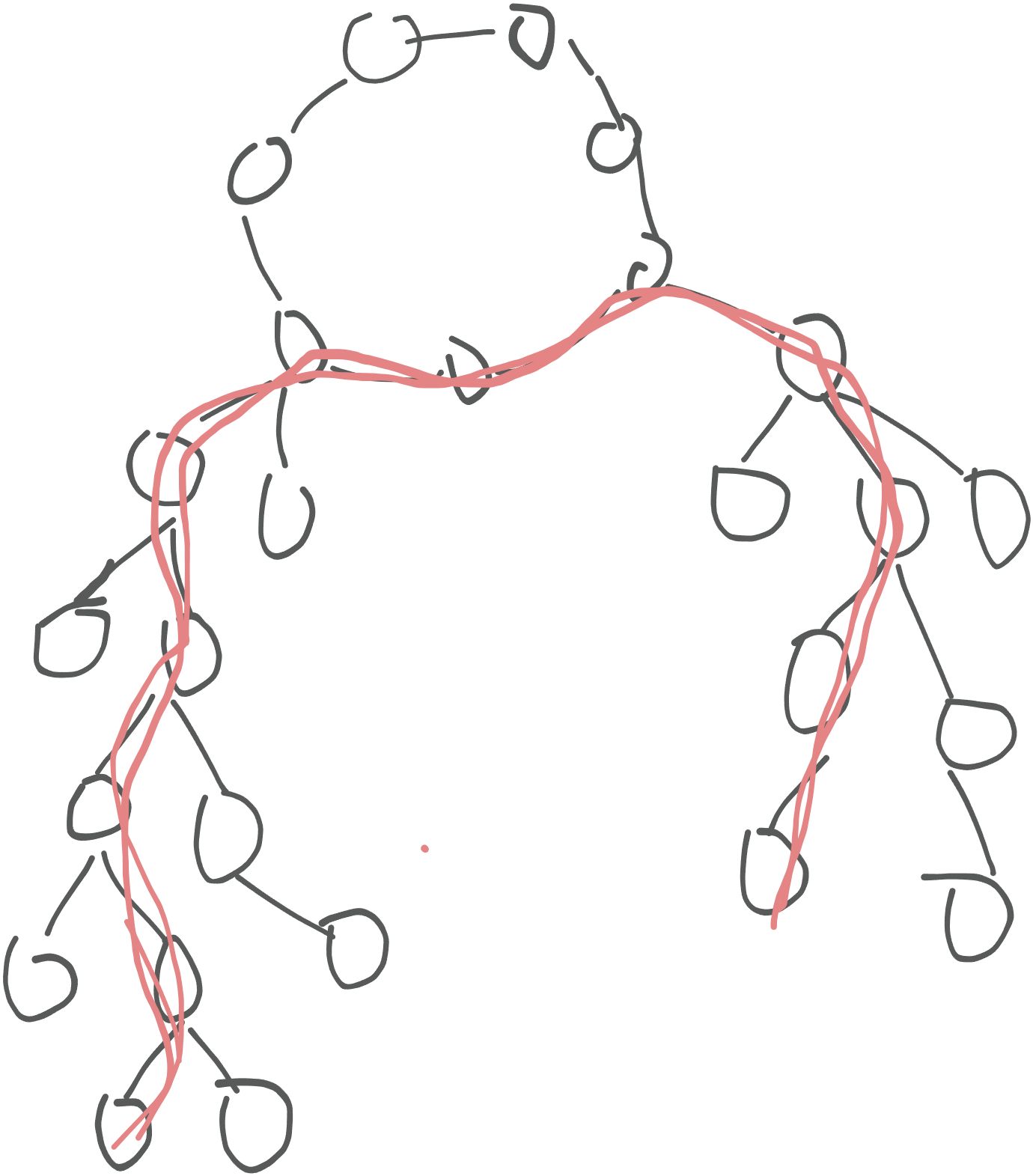
此时答案还是分成两部分:两个子树的最长链 + 环中两点的环中最长距离。
两个子树的最长链通过上面的 dfs 计算都已经知道,环中两点如果枚举的话时间会到\(O(n^2)\)。
优化方案为:把环拆解链,拷贝等长一份,加上上述枚举的两个结点为 x,y,这样在链中就可以用前缀和快速求解 x,y 的环中距离,这个距离为\(sum[y - 1] + dp[y] + (dp[x]-sum[x])\),固定 y ,\(sum[y-1] + dp[y]\)为定值,需要找到最大的\(dp[x]-sum[x]\),x 可能为环中除了 y 的任意一个点,那么选择的范围为 y 往前环的长度个单位,这个区间是一个定长区间,求的是定长区间的一个最大值,采用单调队列快速求解。

code:
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
const int N = 5e5 + 10;
int cnt[N];
bool st[N];
vector<int> edges[N];
int n, t[N], dp[N];
int ans;
vector<int> path;
int cir_len;
void top_sort()
{
queue<int> q;
for(int i = 1; i <= n; i+ )
{
if(cnt[i] == 1) q.push(i);
}
while(!q.empty())
{
int t = q.front(); q.pop();
st[t] = true;
for(auto& x : edges[t])
{
cnt[x]--;
if(cnt[x] == 1) q.push(x);
}
}
}
int dfs1(int x, int fa)
{
int tmp = 0;
for(auto& y : edges[x])
{
if(y == fa || !st[y]) continue;
dfs1(y, x);
// 更新 tmp
tmp = max(tmp, dp[y] + dp[x]);
// 更新 dp[x]
dp[x] = max(dp[x], dp[y]);
// 更新情况一的 ans
ans = max(ans, tmp + t[x]);
}
dp[x] + = t[x];
return tmp;
}
void dfs2(int x)
{
path.push_back(x);
cir_len+ ;
st[x] = true;
for(auto& y : edges[x])
{
if(!st[y]) dfs2(y);
}
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i+ ) cin >> t[i];
for(int i = 1; i <= n; i+ )
{
int x, y; cin >> x >> y;
edges[x].push_back(y);
edges[y].push_back(x);
cnt[x]+ ;
cnt[y]+ ;
}
top_sort();
int len = 0;
for(int i = 1; i <= n; i+ )
if(!st[i])
len + = t[i];
for(int i = 1; i <= n; i+ )
{
if(!st[i])
{
int tmp = dfs1(i, 0);
// 答案的第二种情况
ans = max(ans, tmp + len);
}
}
path.push_back(0);
for(int i = 1; i <= n; i+ )
{
if(!st[i])
{
dfs2(i);
break;
}
}
int m = path.size();
for(int i = 1; i < m; i+ ) path.push_back(path[i]);
// for(auto& x : path) cout << x << " ";
// cout << cir_len << endl;
vector<int> sum(path.size() + 1, 0);
for(int i = 1; i < path.size(); i+ ) sum[i] = sum[i - 1] + t[path[i]];
deque<int> dq; // sum[x - 1] + dp[x]
for(int y = 1; y < path.size(); y+ )
{
while(dq.size() && y - dq.front() + 1 > cir_len) dq.pop_front();
// 答案的第三种情况
if(y > cir_len)
{
int x = dq.front();
ans = max(ans, sum[y - 1] + dp[path[y]] + (dp[path[x]] - sum[x]));
// cout << x << " " << dq.size() << " ";
// cout << y << " " << path[y] << " " << ans << endl;
}
while(dq.size() && dp[path[dq.back()]] - sum[dq.back()] <= dp[path[y]] - sum[y]) dq.pop_back();
dq.push_back(y);
}
cout << ans << endl;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号