25 C++蓝桥杯B组题解
一、移动距离
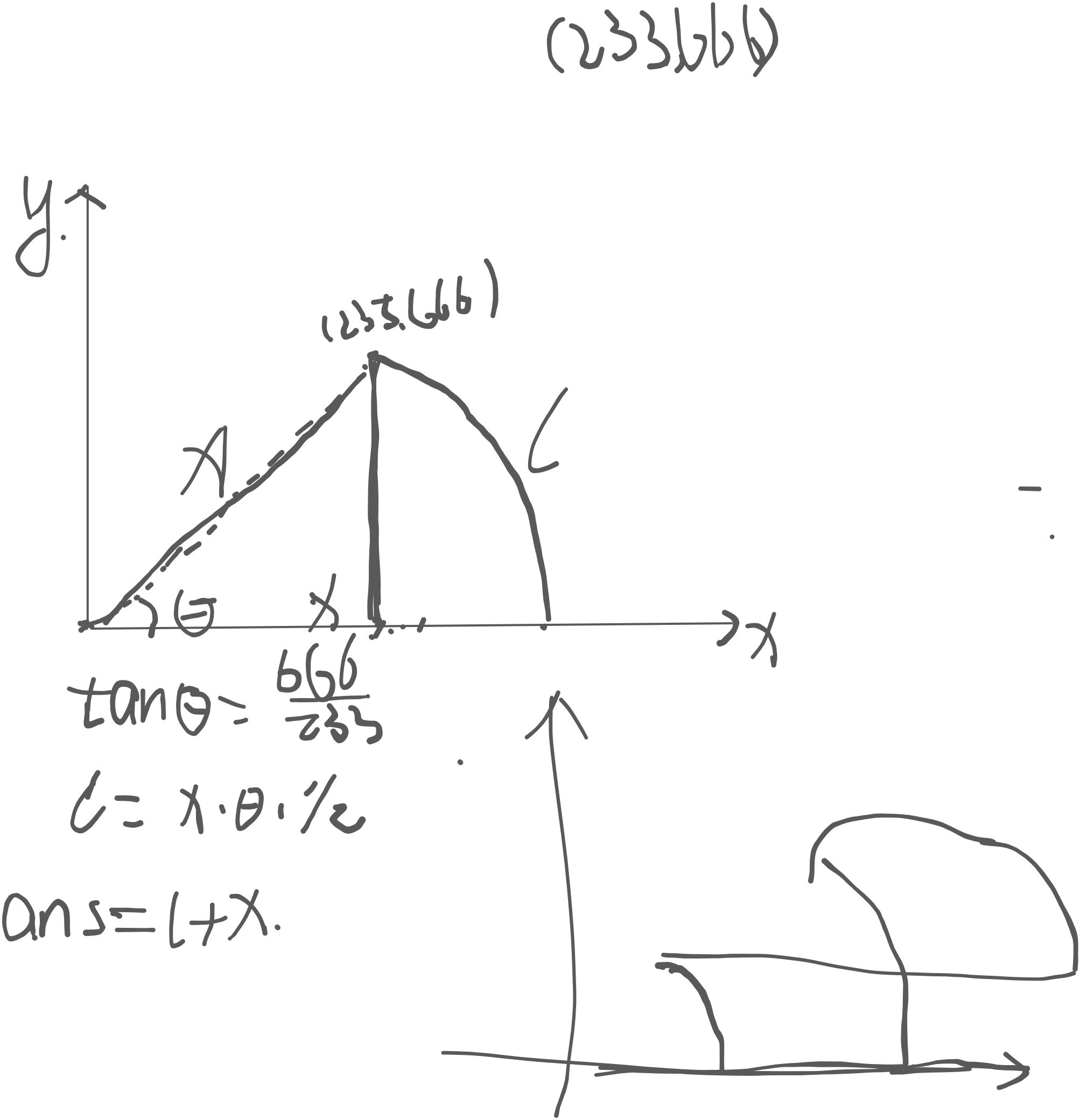
题目大意:小明初始在二维平面的原点 (0,0),他想前往坐标 (233,666)。
现在他有两种移动策略:
- 水平向右移动,即沿着 x 轴正方向移动一定的距离。
- 沿着一个圆心在原点 (0,0)、以他当前位置到原点的距离为半径的圆的圆周移动,移动方向不限(即顺时针或逆时针移动不限)。
【题解】:由于仅仅在水平方向的移动策略仅有 1 ,所以第一步显然只能执行 1 操作,最优操作一定是一次 1 操作然后一次 2 操作。
code:
#include <iostream>
#include <math.h>
using namespace std;
int main()
{
double r = sqrt(233 * 233 + 666 * 666);
double si = atan(666 * 1.0 / 233);
cout << (int)(r + r * si + 0.5) << endl;
return 0;
}
二、客流量上限
题目大意:求 1 - 2025 的排列,满足以下条件:
对于任意位置 i,j,\(i \le j\),选的数为\(A_i,A_j \),\(A_i * A_j \le ij + 2025\)的排列的数量。
【题解】:由于对于一个 i ,j 的取值很多,这种题目暴力搜索显然是不可以的,就去尝试用题目给定的条件去缩小范围。
- 对于 i = j 的情况,\(A_i^2 \le i^2 + 2025\)->\(A_i \le \sqrt{i^2 + 2025}\),其中\(A_i\)为整数。对于这个条件我们可以去进一步缩小\(A_i\)的取值情况。
int main()
{
for(int i = 1; i <= 2025; i++)
{
cout << i << " " << (int)sqrt(i * i + 2025) << endl;
}
return 0;
}

我们会发现,在\(i \ge 1013\),\(A_i \le i\),此时我们把数分为两部分:\(i < 1013\),\(i > 1013\)。根据上述结论,在\(i \ge 1013\)的时候,由于前 1012 个数已经把数都用完了,对于这部分 i ,\(A_i = i\)。
- 现在我们来讨论\(i \le 1012\)的情况,这一部分的取值需要进一步去明确,我们取\(i \le 1012, j \ge 1013\)。
->\(A_i * j \le i * j + 2025\)->\(A_i \le i + \frac{2025}{j} = i+ 1\)。
- 对于\(i= 1,A_i \le 2\)-> 两种选择方案;
- 对于\(i= 2,A_i \le 3\)-> 两种选择方案;
- 对于\(i= 3,A_i \le 4\)-> 两种选择方案;
.... ->\(ans = 2^{1012} \%MOD\)
code:
#include <iostream>
#include <cmath>
using namespace std;
typedef long long LL;
const LL MOD = 1e9 + 7;
LL qpow(LL a, LL b)
{
LL ret = 1;
while(b)
{
if(b & 1) ret = ret * a % MOD;
b >>= 1;
a = a * a % MOD;
}
return ret;
}
int main()
{
cout << qpow(2, 1012) << endl;
return 0;
}
三、可分解的正整数
题目大意:问一个正整数序列能够分解的数的个数,其中分解规则如下:
- 分解成的序列长度要大于等于 3.
- 且分解的序列中的数字是连续递增的整数(可以为负数).
【题解】:显然对于一个非 1 的数都可以分解成 该数 + 一个和为 0 的递增前缀(-2 -1 0 1 2 3)。可以证明 1 不可分解。
code:
#include <iostream>
using namespace std;
int main()
{
int n; cin >> n;
int ans = 0;
for(int i = 1; i <= n; i++)
{
int x; cin >> x;
if(x != 1) ans++;
}
cout << ans << endl;
return 0;
}
四、产值调整
题目大意:对于给定三个初始值 A, B, C,问执行 k 次操作后最后的 A, B, C。
每次操作:\(A^{'} = \frac{B + C}{2}\)\(B^{'} = \frac{A + C}{2}\)\(C^{'} = \frac{A + B}{2}\)。
【题解】:我们可以模拟整个过程,但是 k 很大,会超时,发现在不断平均的过程中,A,B,C 最后会很快趋于一个定值,可以在模拟的时候判断一下。
#include <iostream>
using namespace std;
typedef long long LL;
void solve()
{
LL a, b, c; cin >> a >> b >> c;
LL k; cin >> k;
while(k--)
{
LL A = (b + c) / 2;
LL B = (a + c) / 2;
LL C = (a + b) / 2;
if(A == a && B == b && C == c)
{
break;
}
a = A;
b = B;
c = C;
}
cout << a << " " << b << " " << c << endl;
}
int main()
{
int t; cin >> t;
while(t--) solve();
return 0;
}
五、画展布置
题目描述:给定一个长度为 n 的序列,从中选出 m 个,最小化这选择的 m 个数的\(\sum_{i=1}^{m - 1}\left| B_{i+1}^{2}-B_{i}^{2}\right|\)。
【题解】:显然当序列排序完成后,会包含最优解,此时双指针维护长度为 m 的区间中的上述值。
code:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
typedef long long LL;
int main()
{
int n, k;
cin >> n >> k;
k--;
vector<LL> a(n + 1);
for(int i = 1; i <= n; i++) cin >> a[i];
sort(a.begin(), a.end());
LL ans = 1e18;
LL sum = 0;
int l = 2;
for(int r = 2; r <= n; r++)
{
sum += a[r] * a[r] - a[r - 1] * a[r - 1];
while(r - l + 1 > k)
{
sum -= a[l] * a[l] - a[l - 1] * a[l - 1];
l++;
}
if(r - l + 1 == k)
{
ans = min(ans, sum);
}
}
cout << ans << endl;
return 0;
}
六、水质检测
题目描述:在一个 2 * n 的矩形中,有若干连通块,我们需要找到将这些连通块全部联通的最小路径。
【题解1】:01 BFS ,连接所有的连通块的最短路径,等于从最左边连通块走到最右边连通块的最短路,这是必然的,因为中途的连通块在最初始的连通块经过连通块的字符所在列的时候必然会联通该连通块。
- 当下一个位置是 # 时,路径边权为 0.
- 当下一个位置是 . 时,路径边权为 1.
code:
#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
using namespace std;
const int N = 1e6 + 10;
int dist[2][N];
deque<pair<int, int>> dq;
char g[2][N];
int n;
int dx[] = {0, 0, 1, -1};
int dy[] = {1, -1, 0, 0};
int bfs(int i, int j)
{
dist[i][j] = 0;
dq.push_back({i, j});
int ans = 0;
while(dq.size())
{
auto [x, y] = dq.front(); dq.pop_front();
for(int k = 0; k < 4; k++)
{
int nx = x + dx[k];
int ny = y + dy[k];
if(nx < 0 || nx >= 2 || ny < 0 || ny >= n) continue;
if(g[nx][ny] == '#') ans = max(ans, dist[nx][ny]);
if(dist[nx][ny] != -1) continue;
if(g[nx][ny] == '#')
{
dist[nx][ny] = dist[x][y];
dq.push_front({nx, ny});
}
else
{
dist[nx][ny] = dist[x][y] + 1;
dq.push_back({nx, ny});
}
}
}
return ans;
}
int main()
{
cin >> g[0] >> g[1];
n = strlen(g[0]);
memset(dist, -1, sizeof dist);
for(int j = 0; j < n; j++)
{
if(g[0][j] == '#')
{
cout << bfs(0, j) << endl;
return 0;
}
if(g[1][j] == '#')
{
cout << bfs(1, j) << endl;
return 0;
}
}
return 0;
}
【题解2】:线性dp,本题很像路径类dp,把 # -> 0,. -> 1,就相当于从第一个连通块走到最后一个连通块的最小花费,对于每一个 dp 值,它的值由左侧,上侧\下侧的 dp 值转移,问题在于同列的转移相互依赖,违背了 dp 需要 DAG 的性质,好在本题只有两行,同列的转移可以等效换做前一列的转移。
下面来明确一下 dp 的 状态表示,状态转移方程,初始化,填表顺序,转移方向,答案。
- 状态表示\(dp_{i,j}\):从起始连通块连接到\((i,j)\)位置所需要的最小花费。
- 状态转移方程:
-\(i = 0\),\(dp_{0,j}\)的依赖位置为\((0, j - 1)\)\((1, j-1)\),\(dp_{0,j}=dp_{0,j}+min(dp_{0,j-1}, dp_{1,j-1}+a_{1,j}=='.')\)。
-\(i = 1\),\(dp_{1,j}\)的依赖位置为\((0, j - 1)\)\((1, j-1)\),\(dp_{1,j}=dp_{1,j}+min(dp_{1,j-1}, dp_{0,j-1}+a_{0,j}=='.')\)。
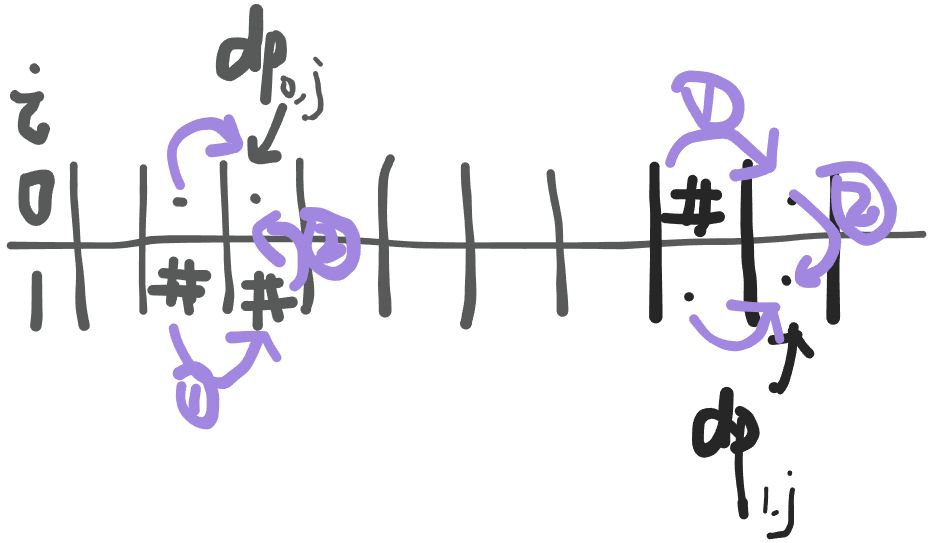
- 初始化:\(a_{i,j} = '.'\)->\(dp_{i,j}=1\),\(a_{i,j} = '\#'\)->\(dp_{i,j}=0\)。
- 转移方式:从最左侧连通块到最右侧连通块,每次转移一列两个值。
- 答案:\(min(dp_{0,j}, dp_{1,j})\),其中 j 为最右连通块所在列(实际上统计最右 # 所在列节即可)。
code:
#include <iostream>
#include <string>
#include <string.h>
using namespace std;
const int N = 1e6 + 10;
char a[2][N];
int dp[2][N];
int main()
{
string s1, s2;
cin >> s1 >> s2;
int n = s1.size();
int r = -1, l = n + 1;
for(int i = 1; i <= n; i++)
{
a[0][i] = s1[i - 1];
a[1][i] = s2[i - 1];
dp[0][i] = a[0][i] == '#' ? 0 : 1;
dp[1][i] = a[1][i] == '#' ? 0 : 1;
if(a[0][i] == '#' || a[1][i] == '#') l = min(l, i), r = max(r, i);
}
if(l > r)
{
cout << 0 << endl;
return 0;
}
for(int j = l + 1; j <= r; j++)
{
dp[0][j] = dp[0][j] + min(dp[0][j - 1], dp[1][j - 1] + (a[1][j] == '#' ? 0 : 1));
dp[1][j] = dp[1][j] + min(dp[1][j - 1], dp[0][j - 1] + (a[0][j] == '#' ? 0 : 1));
}
cout << min(dp[0][r], dp[1][r]) << endl;
return 0;
}
七、生产车间
题目描述:给定一颗 n 个结点的有根树,1 为根节点,对于每个结点有一个权值\(w_i\)
它的涵义为:
- 若 i 为叶子结点,表示该节点能往上提供\(w_i\)的产值。
- 若 i 为非叶节点,表示该节点最多能容纳的产值上限为\(w_i\)。
问根节点最多能收到多少产值?
样例模拟:
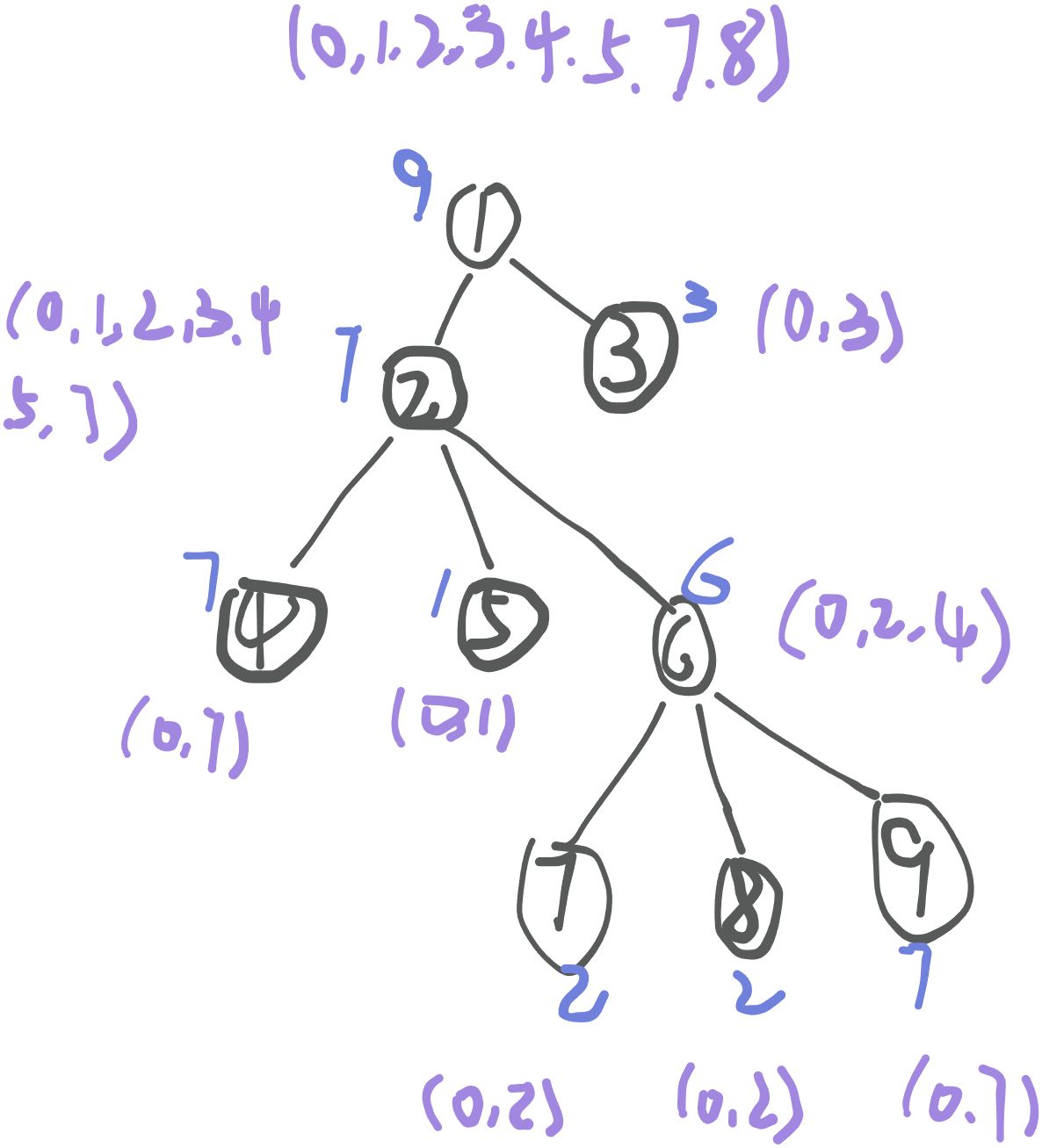
【题解 未优化版本】:树形dp+ 树上(分组)背包。
对于贪心算法,比较容易想到的是,假如对于每一个非叶节点,提供小于等于\(w_i\)最大的权值往上转移,显然这样是不行的,因为这个最大的产值很可能会令根节点的产值溢出,从而把结点答案更新错误。
通过对样例的模拟发现,对于每个结点 i ,更新该节点能得到的最大产值,需要其孩子结点所有的能够提供的产值信息,这显然是一个 树形dp 的过程。因此需要维护每个节点对应的所有能获得所有的产值可能。
转移的过程:每个孩子结点能提供若干个数,从中选择一个,每种选择方案得到一个sum,求出所有的 sum 可能。这是一个分组背包。
到此解法已经很明确了,下面明确以下 dp 的状态表示,状态转移方程,初始化,填表顺序,答案。
对于分组背包:
- 状态表示\(dp_{i,j}\):从前 i 个组中选择,是否能够凑出总产值 j。
- 状态转移方程:\(dp_{i, j} = dp_{i-1,j-k}\),k 去循环 i 组产值的所有可能。
- 初始化:第一个组可能的产值全部设置为 true(由于本题可以选择不选则任何一个产值,\(dp_{1,0} = true\))。
- 填表顺序:i 去循环所有的组,j 去循环\(0\)~\(w_i\),k 去循环每组产值。
对于树上分组背包:
- 状态表示:\(dp_{x,i,j}\):从 x 的子节点所在的可能凑出产值组 i 中选,是否能凑出总产值 j。这样定义的转移方程是 树上dp 和 分组背包 的组合,x 状态属于树形dp,i,j 状态属于分组背包,分组背包可以把 i 这一维度优化掉(如果不优化,后面的转移方程会非常复杂),优化后的状态表示\(dp_{x,j}\):从 x 的子节点所有的可能凑出产值组中选,是否能凑出总产值 j。
- 状态转移方程:\(dp_{x,j}\)=\(dp_{x,j}\)||\((dp_{y,k}\)&&\(dp_{x,j-k})\)。y 为 x 的孩子节点,k 为 y 节点的所有向上提供的可能产值。
- 初始化:
- 对于每个节点可以删除往上提供 0 的产值 ->\(dp_{x,0} = true\)。
- 对于每个叶子节点,往上提供的产值为\(w_i\)->\(dp_{y,w_{y}} = true\),y 为叶结点。
- 转移顺序:树形dp 的用 dfs 去遍历,对于孩子节点的产值,倒序遍历\(w_y\)~ 0 (空间优化)。
- 答案:显然\(dp_x\)中不为 false 的最高位置即是答案。
code:
#include <iostream>
#include <vector>
using namespace std;
const int N = 1e3 + 10;
int n;
int w[N];
bool dp[N][N];
vector<int> edges[N];
void dfs(int x, int fa)
{
for(auto& y : edges[x])
{
if(y == fa) continue;
dfs(y, x);
// 状态转移
for(int j = w[x]; j >= 0; j--)
{
for(int k = 0; k <= min(w[y], j); k++)
{
dp[x][j] = dp[x][j] || (dp[y][k] && dp[x][j - k]);
}
}
}
}
int main()
{
cin.tie(0); cout.tie(0);
ios::sync_with_stdio(false);
cin >> n;
for(int i = 1; i <= n; i++) cin >> w[i];
for(int i = 1; i < n; i++)
{
int x, y; cin >> x >> y;
edges[x].push_back(y);
edges[y].push_back(x);
}
// 初始化dp
for(int i = 1; i <= n; i++)
{
dp[i][0] = true;
if(edges[i].size() == 1 && i != 1) dp[i][w[i]] = true;
}
// 树形dp
dfs(1, 0);
for(int ans = w[1]; ans >= 0; ans--)
{
if(dp[1][ans])
{
cout << ans << endl;
break;
}
}
return 0;
}
时间复杂度:\(O(n^3)\),对于 n = 1000 的规模应该是过不了的,洛谷和蓝桥杯官方的数据有点水。
【题解 优化版本】:bitset 优化。
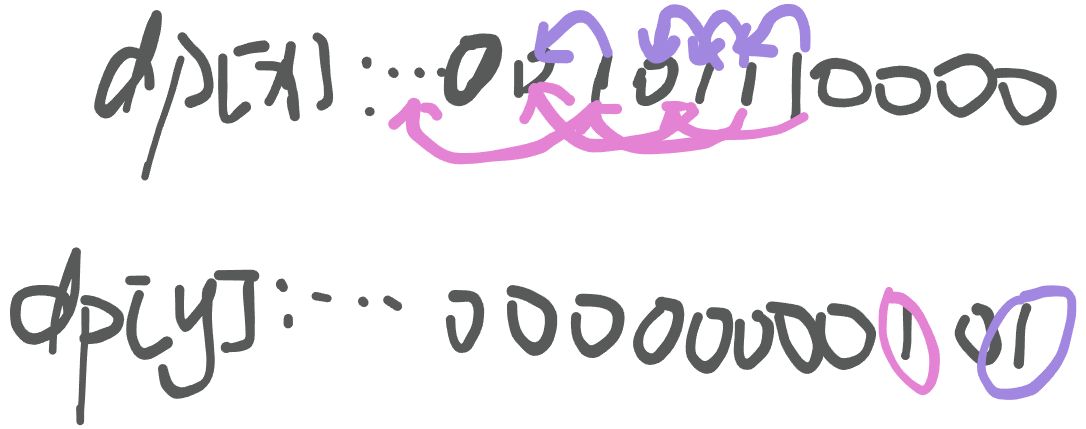
dp 的第二维度表示 j 的产值是否能够凑出来,更新的时候需要同时遍历父节点 x,子节点 y。用 bitset 可以仅仅去遍历 y ,然后打包一次处理父节点 x。
code:
#include <iostream>
#include <vector>
#include <bitset>
using namespace std;
const int N = 1e3 + 10;
int n;
int w[N];
bitset<N> dp[N];
vector<int> edges[N];
void dfs(int x, int fa)
{
for(auto& y : edges[x])
{
if(y == fa) continue;
dfs(y, x);
// for(int j = w[x]; j >= 0; j--)
// {
// for(int k = 0; k <= min(w[y], j); k++)
// {
// dp[x][j] = dp[x][j] || (dp[y][k] && dp[x][j - k]);
// }
// }
// 状态转移
bitset<N> ndp = dp[x];
for(int j = w[y]; j >= 0; j--)
if(dp[y][j])
dp[x] |= ndp << j;
}
}
int main()
{
cin.tie(0); cout.tie(0);
ios::sync_with_stdio(false);
cin >> n;
for(int i = 1; i <= n; i++) cin >> w[i];
for(int i = 1; i < n; i++)
{
int x, y; cin >> x >> y;
edges[x].push_back(y);
edges[y].push_back(x);
}
// 初始化dp
for(int i = 1; i <= n; i++)
{
dp[i][0] = true;
if(edges[i].size() == 1 && i != 1) dp[i][w[i]] = true;
}
// 树形dp
dfs(1, 0);
for(int ans = w[1]; ans >= 0; ans--)
{
if(dp[1][ans])
{
cout << ans << endl;
break;
}
}
return 0;
}
时间复杂度:\(O(\frac{n^3}{64})\)。
八、装修报价
题目大意:给定一个整数序列\(A_1,A_2,A_3,A_4,...,A_n\),在这个整数序列的相邻整数之间插入 -,+,^ 三种运算符中的一个,异或运算优先级最高,其次是加减。问所有可能的组合的和是多少。
样例模拟:
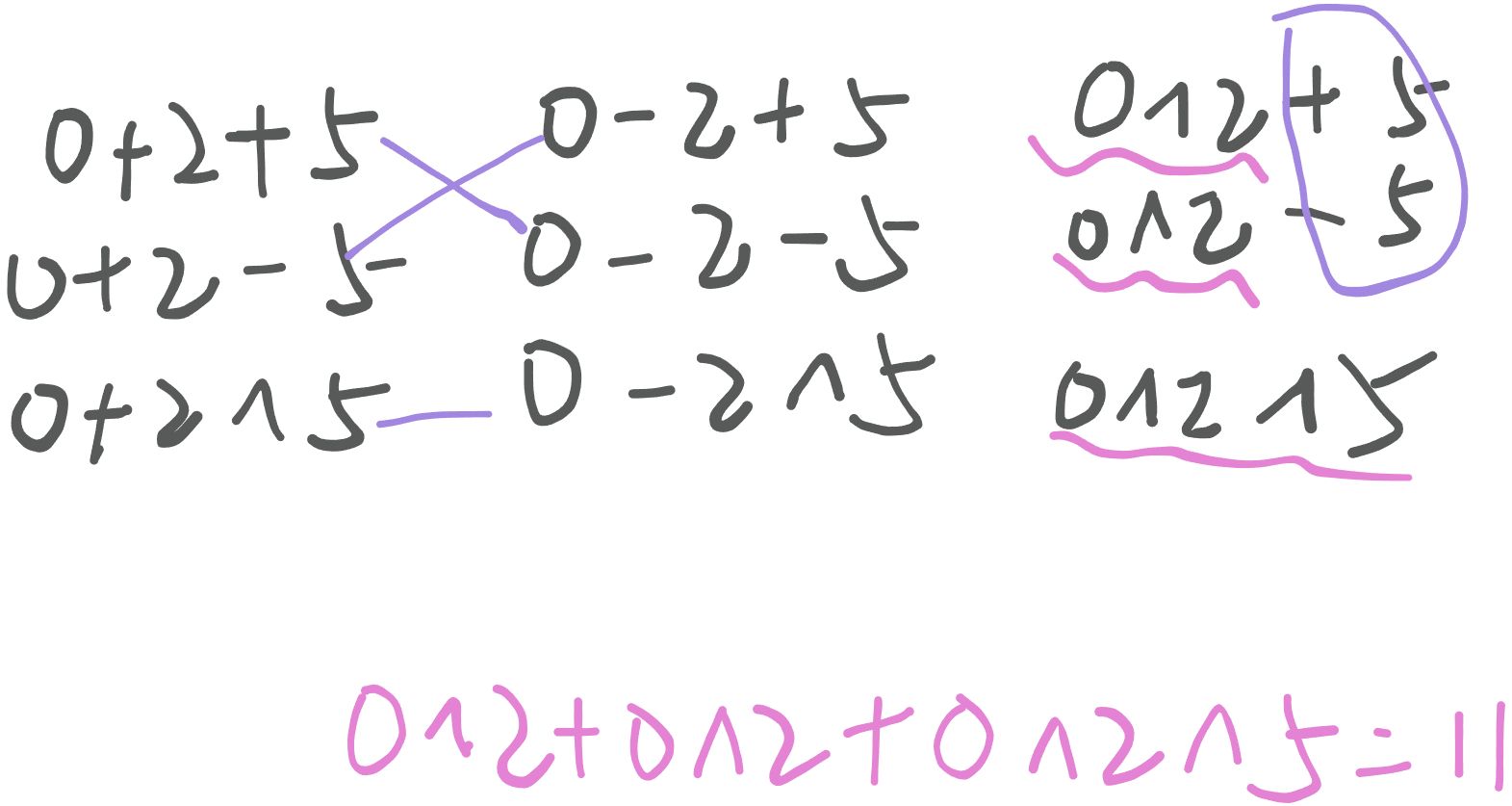
【题解】:
- 对于前缀非 xor 的运算符组合,总有一个组合的结果与之相反,故答案为所有前缀为 xor 的算式之和。
- ans =\(\sum_{i=1}^{n - 1}s_i * 2* 3^{n-i-1}\),\(s_i=A_1\) xor...xor \(A_i\)。
code:
#include <iostream>
using namespace std;
const int MOD = 1e9 + 7;
const int N = 1e5 + 10;
typedef long long LL;
int n;
LL fac[N]; // 3 的幂
LL a[N];
int main()
{
cin >> n;
fac[0] = 1;
for(int i = 1; i <= n; i++) fac[i] = (fac[i - 1] * 3) % MOD;
for(int i = 1; i <= n; i++) cin >> a[i];
LL ans = 0;
LL sn = 0;
for(int i = 1; i < n; i++)
{
sn ^= a[i];
ans = (ans + (sn * 2 % MOD * fac[n - i - 1] % MOD)) % MOD;
}
sn ^= a[n];
ans = (ans + sn) % MOD;
cout << ans << endl;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号