1-5
- 两数之和
给一个数组,和一个target,求数组里两个数字的和为target
一遍哈希表
遍历一遍把值和key放入哈希表中O(n)
查找 target - nums[i] 是否在哈希表中O(1)
vector<int> twoSum(vector<int>& nums, int target) {
unordered_map<int, int> m;
for (int i = 0; i < nums.size(); ++i) {
if (m.count(target - nums[i])) {
return (i, m[target - nums[i]]);
}
m[nums[i]] = i;
}
return {};
}
unorder_map 在 <unorder_map>里
无序查找更快
- 两数相加
给定两个非空链表来表示两个非负整数。位数按照逆序方式存储,它们的每个节点只存储单个数字。将两数相加返回一个新的链表。
很简单的题目
节点忘记new 就直接用构造函数orz
5+5最后一个进位忘记保存
- 无重复字符的最长子串
给定一个字符串,找出不含有重复字符的最长子串长度
输入: "pwwkew"
输出: 3
解释: 无重复字符的最长子串是 "wke",其长度为 3。
请注意,答案必须是一个子串,"pwke" 是一个子序列 而不是子串。
unordered_map<char, int> m;
for (int i = 0; i < len; i++) {
m[s[i]] = i;
cnt = 1;
temp.push_back(s[i]);
for (int j = i + 1; j < len; j++) {
if (m.count(s[j])) break;
else {
m[s[j]] = j;
cnt++;
temp.push_back(s[j]);
}
}
if (cnt > max) {
ans = temp;
max = cnt;
}
temp.clear();
m.clear();
}
s[i]开头的子串寻找,遍历过的进入m,直到找到有重复元素的为止
每换一次开头,清空一次m
大概O(n^2)
(好像用一个普通bool 数组也可以代替map)
- 两个排序数组的中位数
给定两个大小为 m 和 n 的有序数组 nums1 和 nums2 。
请找出这两个有序数组的中位数。要求算法的时间复杂度为 O(log (m+n)) 。
你可以假设 nums1 和 nums2 不同时为空。
方法一:
算法复杂度O(m+n)的方法,很显然是合并两个数组
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
vector<int> num3;
vector<int>::iterator it1, it2;
it1 = nums1.begin();
it2 = nums2.begin();
while (it1 != nums1.end() || it2 != nums2.end()) {
if (it1 != nums1.end() && it2 != nums2.end()) {
if (*it1 < *it2) {
num3.push_back(*it1);
it1++;
}
else {
num3.push_back(*it2);
it2++;
}
}
else if (it1 != nums1.end() && it2 == nums2.end()) {
num3.push_back(*it1);
it1++;
}
else if (it1 == nums1.end() && it2 != nums2.end()) {
num3.push_back(*it2);
it2++;
}
}
double ans;
int len = num3.size();
if (len % 2 == 0) {
ans = (num3[len / 2]* 1.0 +1.0*num3[len / 2 - 1]) / 2;
}
else
ans = num3[int(len / 2)];
return ans;
}
![]()
测试样例也太弱了
方法二
题目要求O(log(m+n))分治
中位数的划分作用是,将一个数组划成两个长度相等子集,一个子集元素总是大于另一个子集元素。
![]()
将AB 划分为连长度相同的两个部分,且其中一部分元素总是大于另一部分元素那么
![]()
就可以求得中位数
要确保这两个条件,只需要
![]()
1的意思是前半部分数量 等于后半部分数量
确保n大于等于m
先不考虑临界值
我们需要在[0,m]上搜索I 使
前半部分最大数可能是A[i - 1] 或 B[j-1] 后半部分最小数可能是A[i]或B[j]
![]()
在[imin, imax]中搜索
![]()
增大i还是减小i的决定条件是
(1)
![]()
找到目标停止搜索
(2)
![]()
意味着A[i]太小了
i++
(3)
![]()
意味着i太大了
i--
![]()
![]()
处理边界条件
![]()
![]()
class Solution {
public double findMedianSortedArrays(int[] A, int[] B) {
int m = A.length;
int n = B.length;
if (m > n) { // to ensure m<=n
int[] temp = A; A = B; B = temp;
int tmp = m; m = n; n = tmp;
}
int iMin = 0, iMax = m, halfLen = (m + n + 1) / 2;
while (iMin <= iMax) {
int i = (iMin + iMax) / 2;
int j = halfLen - i;
if (i < iMax && B[j-1] > A[i]){
iMin = i + 1; // i is too small
}
else if (i > iMin && A[i-1] > B[j]) {
iMax = i - 1; // i is too big
}
else { // i is perfect
int maxLeft = 0;
if (i == 0) { maxLeft = B[j-1]; }
else if (j == 0) { maxLeft = A[i-1]; }
else { maxLeft = Math.max(A[i-1], B[j-1]); }
if ( (m + n) % 2 == 1 ) { return maxLeft; }
int minRight = 0;
if (i == m) { minRight = B[j]; }
else if (j == n) { minRight = A[i]; }
else { minRight = Math.min(B[j], A[i]); }
return (maxLeft + minRight) / 2.0;
}
}
return 0.0;
}
}
- 最长回文子串
- 把串逆序寻找最长公共子串
X[i] == Y[j],dp[i][j] = dp[i-1][j-1] + 1
X[i] != Y[j],dp[i][j] = 0
巨大的坑
![]()
需要检查字串索引与反向字串的原索引是否相同
(不懂找)
- 动态规划
性质:回文串去掉头尾还是回文串
![]()
dp[j][i]表示 j 到 i 是否是回文串
const int n = s.size();
if (n == 0) return "";
bool dp[n][n];
memset(dp, 0, sizeof(dp));
int maxlen = 1; //保存最长回文子串长度
int start = 0; //保存最长回文子串起点
for (int i = 0; i < n; ++i)
{
for (int j = 0; j <= i; ++j)
{
if (i - j < 2)
{
dp[j][i] = (s[i] == s[j]);
}
else
{
dp[j][i] = (s[i] == s[j] && dp[j + 1][i - 1]);
}
if (dp[j][i] && maxlen < i - j + 1)
{
maxlen = i - j + 1;
start = j;
}
}
}
return s.substr(start, maxlen);
- 中心扩展法
把一个字母作为中心,向两边扩展
分奇数偶数
以上方法都是O(n^2)
还有一个复杂度为 O(n)O(n) 的 Manacher 算法
- Manacher 算法





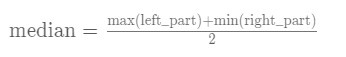

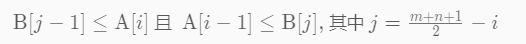
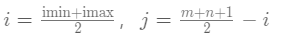

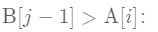
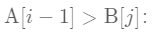
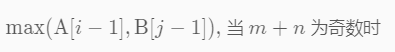
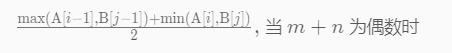



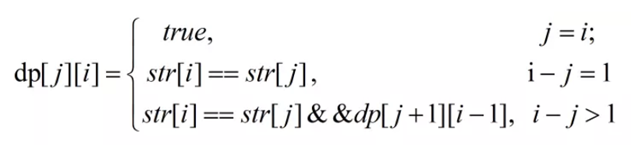

 浙公网安备 33010602011771号
浙公网安备 33010602011771号