[待验证]高中物理：旋转体动能

一质量分布均匀的圆盘，圆心中间处加一转轴（如图）

圆盘质量为\(M\)，半径为\(R\)，不考虑圆盘的厚度。

不考虑一切阻力。

施加力\(F\)，作用于圆盘，使圆盘获得角速度。

当角速度达到\(\omega\)时取消力\(F\)。

接下来圆盘会以角速度\(\omega\)状态持续旋转下去。

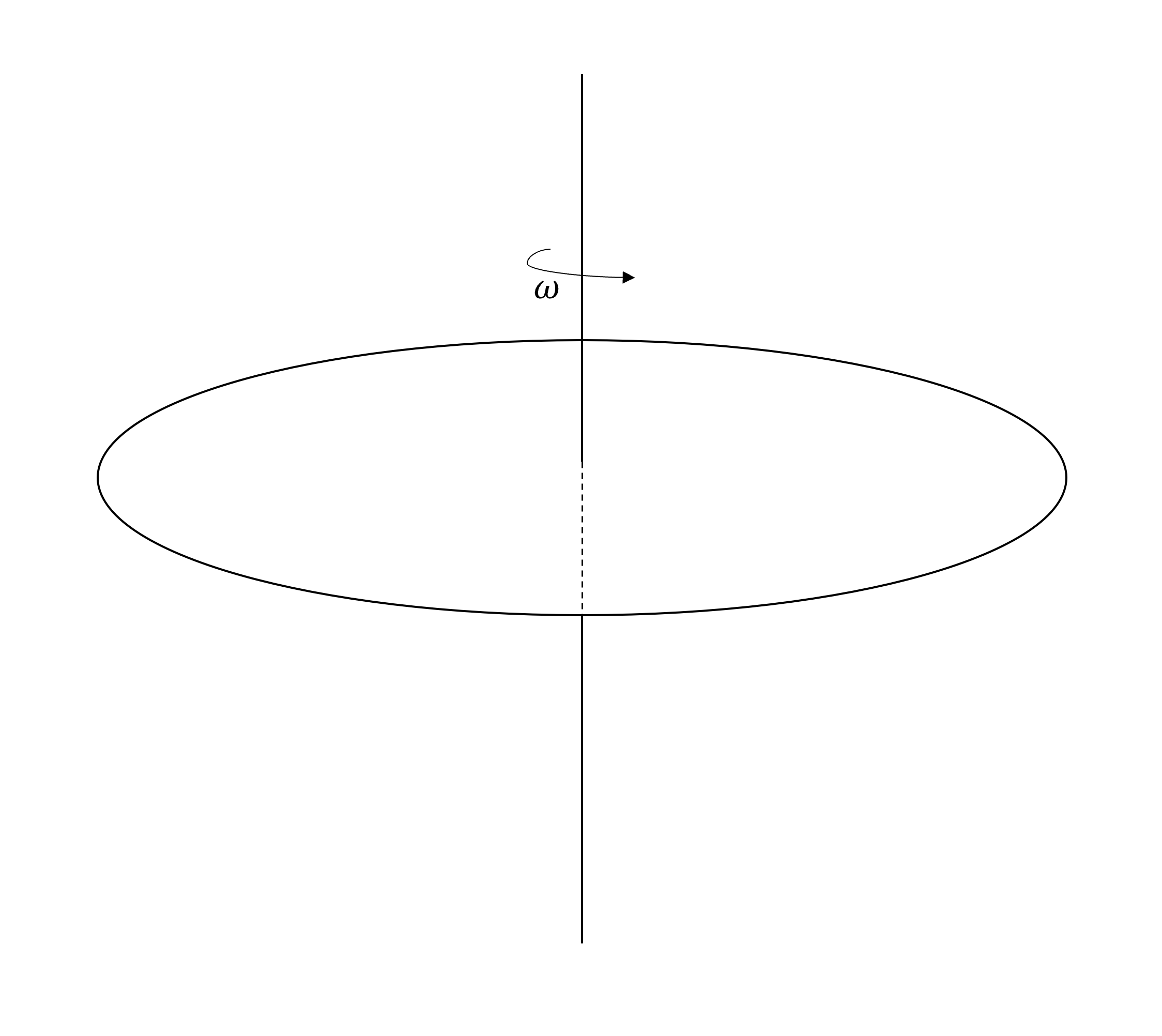
此时该圆盘获得的动能为多少？

将圆盘分为 \(n\) 个小圆环，记 \(r=\frac{R}{n}\)

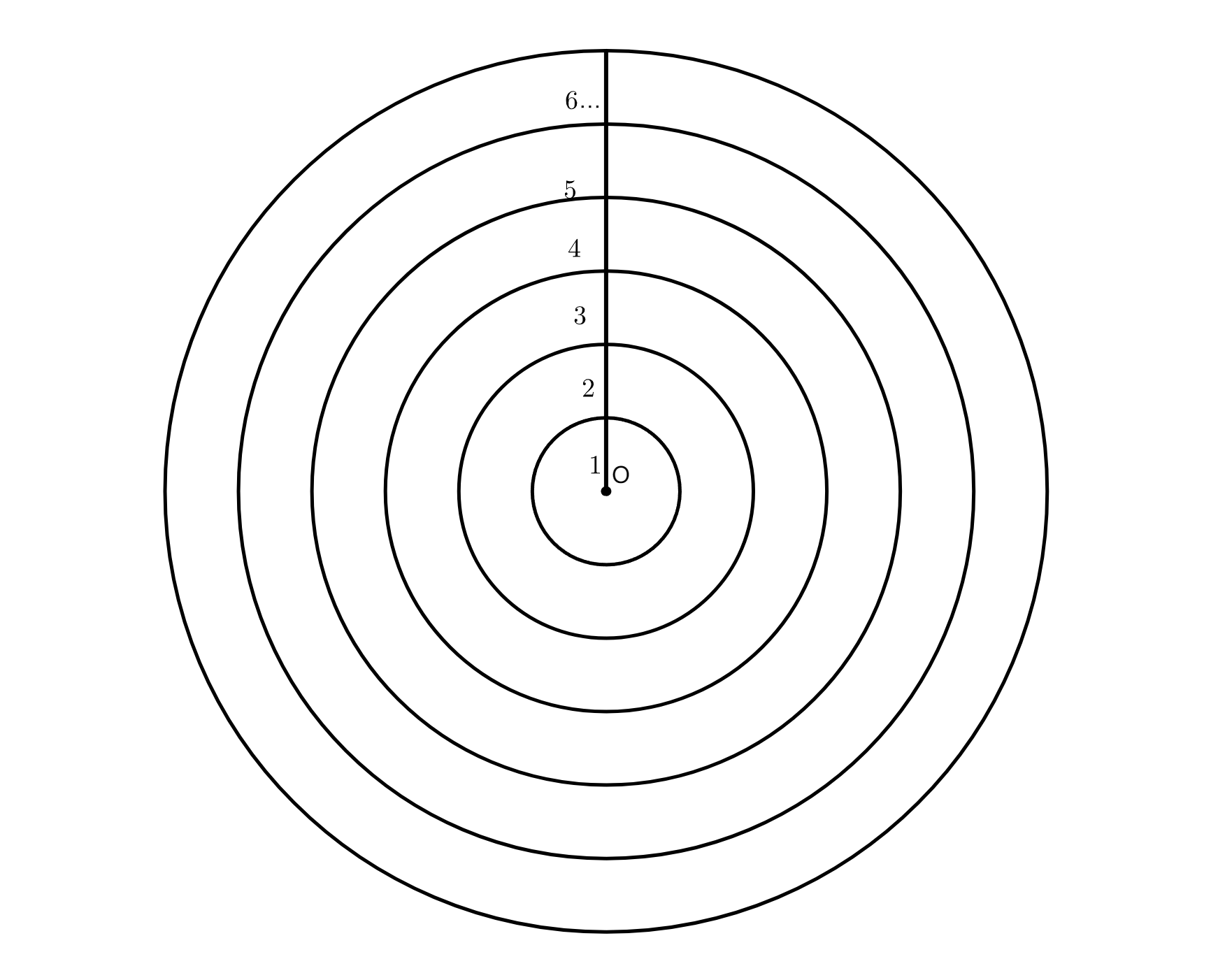
则第 \(i\) 个小圆环的面积为 \(\pi (ir)^2-\pi (i-1)^2 r^2\)

即 \(S_{i} = 2i\pi r^2 - \pi r^2\)

由于质量分布均匀，面积占比比等于质量占比

\[m_{i} = M\times \frac{2i\pi r^2 - \pi r^2}{\pi R^2} \]

此时由于最后会使 \(n \to +\infin\) ，所以可以看成无数的线和最里面的点，每一个线的动能中的速度用这个环这一层的速度为代表。

\[E_{k i} = \frac{1}{2} \times m_{i} \times (\omega r i)^2 \\\ \implies E_{k i} = (2i^3 - i^2) \times \frac{M\omega R^2}{2n^4} \]

所以

\[\sum_{i=1}^{n}{E_{ki}} = \frac{M\omega ^2 R^2}{2n^4} \times (2\sum_{i=1}^{n}{i^3} - \sum_{i=1}^{n}{i^2}) \]

并且由高阶数列知识可以推导出

\[\sum_{i=1}^{n}{i^2} = \frac{2n^3+3n^2+n}{6} \\\ \sum_{i=1}^{n}{i^3} = \frac{n^4+2n^3+n^2}{4} \]

事实上我用了好长时间推导这两个柿子...

所以易得出：

\[\sum_{i=1}^{n}{E_{ki} = M\omega ^2 R^2 \times (\frac{1}{4} + \frac{4n^2 - 1}{12n^3})} \]

\[\lim_{n\to +\infin}{\sum_{i=1}^{n}{E_{ki} = \frac{1}{4} M\omega^2 R^2}} \]

嗯，简洁地有点诡异，估计有问题