11.22-11.29干了什么

Merlin 日记

11.21

Day1 早晨在早读的时候被突然通知家长在门口等着（

家长说做完就告诉班主任了（？我怎么没收到通知

鉴定为：S_D 太 忙 了 导 致 的 。

模拟赛被薄纱垫底。

miaomiao 说这个难度不适合我们（

11.22

这是历史重演的第一天

被踢出正常模拟赛了，降级。

T3 写的指数暴力，但是我自己给自己限制了个 \(n \le 5\) 没想到他可以跑到 \(9\) 遂挂 \(20\) 分。

T1情景剧

第一次知道 h.hszxoj.com 这个OJ交 MLE 的代码居然显示全 RE，T1用 ST表 乱搞暴力表开大了MLE保龄

题目信息

• 时间限制：\(1s\)
• 空间限制：\(256MiB\)

题目描述

白浅妹妹要在班上的\(n\)个同学中请一些学号连续的同学上讲台表演情景剧。用\(h_i\)表示学号为\(i\)的同学的身高，定义一个情景剧的有趣程度为上台的同学中最高的身高\(\times\)最矮的身高\(\times\)上台的人数。白浅妹妹想知道有趣程度最大为多少。大样例: sample.zip。

输入格式

1. 第一行包含一个正整数\(n\)，表示班级里同学的人数。
2. 第二行包含\(n\)个用空格隔开的正整数\(h_i\)，表示学号为\(i\)的同学身高为\(h_i\)。

输出格式

输出情景剧最大的有趣程度。

样例

样例1输入

\(9\)

\(5\ 11\ 15\ 17\ 19\ 3\ 19\ 9\ 4\)

样例1输出

\(855\)

说明

让学号为\([3,5]\)区间内的同学表演。

备注

1. 对于\(30\%\)的数据，满足\(n\leq10^3\)。
2. 对于\(60\%\)的数据，满足\(n\leq10^5\)。
3. 对于\(80\%\)的数据，满足\(n\leq10^6\)。
4. 对于\(100\%\)的数据，满足\(n\leq2\times10^6\)，\(h_i\leq10^9\)。

假设已找到了区间最小值 \(h_{i}\) 在保证区间中 \(h_{i}\) 为最小值的前提下，扩展区间肯定是越长越好。

那么就需要找到 以 \(h_{i}\) 为最小值的最大区间 \([l,r]\) 。

是不是感觉学过？

tgoj单调栈

stack < int > s;
s.push(1);
a[n + 1] = - 1;
for (int i = 2 ; i <= n + 1 ; i ++)
{
    while (!s.empty() and a[s.top()] > a[i])
    {
        posR[s.top()] = i;
        s.pop();
    }
    s.push(i);
}

先往最后放上一个不可能有人比他更小的值 \(-1\) 防止找不到右边界。

\(posR[i]\) 就是以 \(a[i]\) 为最小值最远的右边界。

把这个代码里的 \(a\) 数组翻转过来就可以求得 \(posL\)。

至此，预处理完之后枚举最小值（位置）然后扩展到最大区间，使用神奇ST表查询当前区间的最大值，统计答案。

预处理复杂度 \(O(n\text{log}n)\) 枚举复杂度 \(O(n)\) ，查询复杂度 \(O(1)\) ，总复杂度为 \(O(n\text{log}n)\) 。

欸？\(\text{\color{red}内存限制 256MiB}\) ST表就恶心在这， \(2e6 \times 25\) 个int需要多少啊。。。

弃ST表（怒）

欸，，

ST表卡边嘿嘿嘿

T2修改01序列

题目信息

• 时间限制：\(1s\)
• 空间限制：\(256MiB\)

题目描述

长度为\(n\)的只包含\(0\)和\(1\)的序列，你可以对它进行多次操作。在每次操作中，你都可以选择一个数字\(0\)变成\(1\)，或者选择一个数字\(1\)变成\(0\)，使得最终局面满足如下特点：对于任意相邻的两个\(1\)，它们在序列中的距离都是\(d\)的倍数，给定\(d\)，求最小操作次数。

输入格式

1. 第一行输入两个正整数\(n\)，\(d\)。
2. 第二行输入\(n\)个用空格隔开的数字，表示题目所描述的序列。

输出格式

输出一个数，表示最小操作次数。

样例

样例1输入

\(5\ 2\)

\(0\ 1\ 0\ 0\ 1\)

样例1输出

\(1\)

说明

将任何一个\(1\)变成\(0\)，这样就没有相邻的\(1\)了，自然也满足题目要求。

样例2输入

\(8\ 2\)

\(1\ 0\ 1\ 0\ 0\ 0\ 1\ 1\)

样例2输出

\(1\)

说明

将最后一个\(1\)变成\(0\)，这样序列变为\([1,0,1,0,0,0,1,0]\)，\(1\)的位置分别是\([1,3,7]\)，其中\(1\)和\(3\)的距离是\(2\)的倍数，\(3\)和\(7\)的距离也是\(2\)的倍数。

备注

1. 对于测试点\(1\)：\(1\leq n\leq10^5\)，\(d = 1\)。
2. 对于测试点\(2\sim3\)：\(1\leq n\leq10^5\)，\(d = 2\)。
3. 对于测试点\(4\sim5\)：\(1\leq d\leq n\leq10^3\)。
4. 对于测试点\(6\sim10\)：\(1\leq d\leq n\leq10^5\)。

bro场切

"所有相邻的两个 \(1\) 之间的间距为 \(d\) 的倍数" \(\iff\) "所有 \(1\) 之间的距离都是 \(d\) 的倍数"。

所以假设两个 \(1\) 之间的距离非法，即不是 \(d\) 的倍数，那么再多加些 \(1\) 他们之间的距离仍然不变，所以仍然不满足 "所有相邻的两个 \(1\) 之间的间距为 \(d\) 的倍数" 的充要条件 "所有 \(1\) 之间的距离都是 \(d\) 的倍数"。

所以我们只进行把 \(1\) 变成 \(0\) 的操作。

不妨关注每个 \(1\) 的 绝对位置 ，比如说在数组里的下标

那么所有的合法的位置必须是 \(k \times d + \Delta x \text{（偏移量）},k \in \N\)

所以枚举 \(\Delta x\) 然后找到所有合法位置上的 \(1\) ，可知所在非法位置的 \(1\) 的数量，即需要操作的次数。

Code Link

大佬做法：

for (int i = 1 ; i <= n ; i ++)
{
    cin >> x;
    if (x)
    {
        cnt ++;
        ton[i % d] ++;
        maxn = max(maxn, ton[i % d]);
    }
}
cout << cnt - maxn;

其实就是把 \(1\) 都分类，分成偏移量不同的情况然后统计每一种偏移量中 \(1\) 的个数，和前面的代码是一样的想法，实现比较高级。

T1字符串构造机

题目信息

• 时间限制：\(1s\)
• 空间限制：\(256MiB\)

题目描述

B酱发明了通过输入LCP（Longest Common Prefix，最长公共前缀）信息，输出由非负整数构成的字符串\(S\)的字符串构造机。将\(S\)的字符从\(1\)开始依次编号，设\(n = |S|\)，记\(S_{i,j}\)表示\(S\)的第\(i\)个字符到第\(j\)个字符构成的子串，定义

\[LCP(i,j)=\max_{i + k\leq n,j + k\leq n,S_{i,i + k}=S_{j,j + k}}\{k + 1\} \]

为了测试字符串构造机，B酱输入了字符串长度\(n\)和\(m\)条如下形式的信息：

\[LCP(x_i,y_i)=z_i \]

B酱的字符串构造机需要输出所有满足条件的字符串中，字典序最小的一个。

输入格式

1. 第一行两个整数\(n\)，\(m\)，表示字符串长度、信息个数。
2. 然后\(m\)行，每行三个整数\(x_i\)，\(y_i\)，\(z_i\)，描述一条信息，保证\(x_i + z_i - 1\)，\(y_i + z_i - 1\leq n\)。

输出格式

输出满足条件的字典序最小的字符串，两个字符（非负整数）之间用空格隔开，如果不存在这样的字符串，输出一行一个整数\(-1\)。

样例

样例1输入

\(3\ 2\)

\(1\ 2\ 0\)

\(1\ 3\ 1\)

样例1输出

\(0\ 1\ 0\)

样例2输入

\(3\ 2\)

\(1\ 2\ 0\)

\(1\ 2\ 1\)

样例2输出

\(-1\)

数据范围与提示

对于所有数据点\(1\leq m\leq1000\)，下面给出每个数据点的限制：

##	\(n\)	特殊性质
1	5	无
2	6	无
3	7	无
4	9	无
5	30	答案为\(-1\)
6	100	无
7	200	\(z_i = 0\)
8	1000	\(z_i = 0\)
9	1000	无
10	1000	无

踩坑记录：这个所谓的"输出满足条件的字典序最小的字符串，两个字符（非负整数） 之间用空格隔开" 说的不是只能用'0' ~ '9' .....无语了..... \(\text{(.\_. \ \ \ )}\)

先将题意的 \(m\) 个关系转换为若干位置的数字相同和若干位置的数字不同，构造满足这些条件的数列。

\(LCP(x_i,y_i)=z_i\) 其实就是 \(\forall k \in [0, z_i - 1]，S_{x_{i} + k}=S_{y_{i} + k}\) 且 \(S_{x_{i} + z_{i}} \neq S_{y_{i} + z_{i}}\) 。

不难看出题目的特殊性质 "保证 \(z_{i}=0\) " 就是在说给出了 \(m\) 个不能相等的位置 \(x_{i}，y_{i}\) 。

必须相等的位置用冰茶几维护成连通块，必须不相等的位置开一个 图 给这两个位置的点连上边，方便后续直接访问和谁不能相等。

cin >> role[i].x >> role[i].y >> role[i].z;
for (int j = 0 ; j < role[i].z ; j ++)
{
    fa[fid_fa(role[i].x + j)] = fa[role[i].y + j];
}

判断无解：遍历 \(1\sim m\) ，若 \(\exist father[S_{x_{i} + z_{i}}] = father[S_{y_{i} + z_{i}}]\) ，则无解。

放数：连通块已经维护好了，那么我们只需要往各个块的根节点放数就好了，我们记录 \(ans\) 数组为点对应填的答案（可能只有根会有数），初始时都设置成 \(-1\) 表示我们还没钦定填什么。这个过程用代码来描述刚好（额，不太会表述）

for (int i = 1 ; i <= n ; i ++)
{
    if (ans[i] == -1) // 这个是为了把当儿子的点给忽略掉，不然就会被覆盖上更大的和爹不一样的数
    {
        for (int j = 0 ; j <= n ; j ++) // 此时j是所有可以填的数
        {
            vis[j] = false; // false状态是还可以填
        }
        for (auto &v : G[fid_fa(i)]) // 给所有已填过的不能和当前i一样的点所填的数打上标记
        {
            if (ans[v] != -1)
            {
                vis[ans[v]] = true;
            }
        }
        for (int j = 0 ; j <= n ; j ++) // 从小到大开始找还有那些数可以填上
        {
            if (vis[j] == false)
            {
                ans[fid_fa(i)] = j;
                break;
            }
        }
    }
    cout << ans[fid_fa(i)] << ' ';
}

Code Link

T2忍者小队

题目信息

1. 时间限制：\(1s\)
2. 空间限制：\(512MiB\)

题目描述

木叶村现役有\(n\)位忍者，第\(i\)位忍者的战斗力为\(s_i\)，用集合\(S\)来表示木叶村所有的现役忍者。一支忍者小队可以用集合\(S_0\)表示，该小队的战斗力为\(S_0\)中所有忍者的战斗力的最大公约数。为了方便任务调度，现在火影想知道\(\forall k\in[1,m]\)，\(\min\{|S_0|\}\)，\(\max\{|S_0|\}\)，即如果需要组建一支战斗力为\(k\)的忍者小队，最少/最多需要多少名忍者。

输入格式

1. 第一行两个正整数\(n\)，\(m\)，含义如题所示。
2. 第二行\(n\)个正整数\(S_{1\sim n}\)，表示木叶村现役忍者们的战斗力。

输出格式

输出共\(m\)行。对于\(\forall k\in[1,m]\)，第\(k\)行输出两个整数\(a\)，\(b\)，其中\(a = \min\{|S_0|\}\)，\(b = \max\{|S_0|\}\)。如果对于当前的\(k\)，无法组成战斗力恰好为\(k\)的忍者小队，输出两个\(-1\)。

样例

样例1输入

\(7\ 5\)

\(30\ 60\ 21\ 42\ 70\ 15\ 30\)

样例1输出

\(3\ 7\)

\(3\ 5\)

\(2\ 6\)

\(-1\ -1\)

\(2\ 5\)

样例2输入

\(3\ 6\)

\(24\ 6\)

样例2输出

\(-1\ -1\)

\(1\ 3\)

\(-1\ -1\)

\(1\ 1\)

\(-1\ -1\)

\(1\ 1\)

数据范围与提示

1. 对于所有数据，满足\(1\leq n,m\)，\(s_i\leq3\times10^5\)，\(m\leq\max\{s_i\}\)。
2. 子任务编号、分值、\(n\)及特殊性质如下：

子任务编号	分值	\(n\)	特殊性质
1	20	20	无
2	20	\(\leq100\)	\(\sum s_i\leq4\times10^2,m\leq10\)
3	20	\(\leq2\times10^3\)	\(m\leq10\)
4	40	\(\leq3\times10^5\)	无

不会，寄

11.23

这是历史重演的一天。Merlin_Meow 和 gzxworld 再一次被踢出了模拟赛进度。----- Merlin 日记

上午是喵喵给的 DP 专题 ，除去一橙全是蓝紫黑，一上午开出来三道。（全是蓝，没动紫和黑）

另外 Merlin 学会了 打块 。

CF1392A Omkar and Password

题面翻译

题目描述

多组询问，每次给出一个长度为 \(n\) 的序列 \(a\)，对于两个相邻的且不相同的数，你可以将他们合并起来，即将这两个数替换成它们的和。

注意到，你每次进行一次操作后，序列长度会 \(-1\)，现在你可以随意进行若干次操作，问最后序列长度最短是多少。

输入格式

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 100 $ ). Description of the test cases follows.

The first line of each test case contains an integer $ n $ ( $ 1 \leq n \leq 2 \cdot 10^5 $ ) — the length of the password.

The second line of each test case contains $ n $ integers $ a_{1},a_{2},\dots,a_{n} $ ( $ 1 \leq a_{i} \leq 10^9 $ ) — the initial contents of your password.

The sum of $ n $ over all test cases will not exceed $ 2 \cdot 10^5 $ .

输出格式

For each password, print one integer: the shortest possible length of the password after some number of operations.

样例 #1

样例输入 #1

2
4
2 1 3 1
2
420 420

样例输出 #1

1
2

提示

In the first test case, you can do the following to achieve a length of $ 1 $ :

Pick $ i=2 $ to get $ [2, 4, 1] $

Pick $ i=1 $ to get $ [6, 1] $

Pick $ i=1 $ to get $ [7] $

In the second test case, you can't perform any operations because there is no valid $ i $ that satisfies the requirements mentioned above.

假设最大的数是 \(p\)，那么 \(p\) 可以和别人合并成 \(q\)，因为 \(\forall a_{i} > 0\) 所以 \(q > p\)，这时 \(q\) 又是唯一一个最大的数了，所以可以一直合并。

结论：当所有数都相等的的时候答案是 \(n\) ，否则答案是 \(1\)。

---

CF1628D1 Game on Sum (Easy Version)

题面翻译

Alice 和 Bob 正在玩一个游戏，游戏分为 \(n\) 个回合，Alice 和 Bob 要轮流对一个数 \(x\) 进行操作，已知这个数初始值是 \(0\)。

具体每个回合的行动规则如下：

1. Alice 选择一个在区间 \([0,k]\) 之间的实数 \(t\)。
2. Bob 可以选择让 \(x\) 变成 \(x+t\) 或者 \(x-t\)，但是 Bob 在 \(n\) 个回合之内至少选择 \(m\) 次让 \(x\) 变成 \(x+t\)。

Alice想让最终的 \(x\) 最大，Bob 想让最终的 \(x\) 最小。

已知双方均采用最优策略，求最终的 \(x\) 值（对 \(10^9+7\) 取模）。

数据范围保证：\(1\le m\le n\le 2000,k < 10^9+7\)。

输入格式

The first line of the input contains a single integer $ t $ ( $ 1 \le t \le 1000 $ ) — the number of test cases. The description of test cases follows.

Each test case consists of a single line containing the three integers, $ n $ , $ m $ , and $ k $ ( $ 1 \le m \le n \le 2000, 0 \le k < 10^9 + 7 $ ) — the number of turns, how many of those turns Bob has to add, and the biggest number Alice can choose, respectively.

It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 2000 $ .

输出格式

For each test case output a single integer number — the score of the optimal game modulo $ 10^9 + 7 $ .

Formally, let $ M = 10^9 + 7 $ . It can be shown that the answer can be expressed as an irreducible fraction $ \frac{p}{q} $ , where $ p $ and $ q $ are integers and $ q \not \equiv 0 \pmod{M} $ . Output the integer equal to $ p \cdot q^{-1} \bmod M $ . In other words, output such an integer $ x $ that $ 0 \le x < M $ and $ x \cdot q \equiv p \pmod{M} $ .

样例 #1

样例输入 #1

7
3 3 2
2 1 10
6 3 10
6 4 10
100 1 1
4 4 0
69 4 20

样例输出 #1

6
5
375000012
500000026
958557139
0
49735962

提示

In the first test case, the entire game has $ 3 $ turns, and since $ m = 3 $ , Bob has to add in each of them. Therefore Alice should pick the biggest number she can, which is $ k = 2 $ , every turn.

In the third test case, Alice has a strategy to guarantee a score of $ \frac{75}{8} \equiv 375000012 \pmod{10^9 + 7} $ .

In the fourth test case, Alice has a strategy to guarantee a score of $ \frac{45}{2} \equiv 500000026 \pmod{10^9 + 7} $ .

Bob想让结果尽量小，所以他肯定会恰好卡边选择 \(m\) 次加法操作，因为多选加法会使结果变大产生劣势。

先玩个小样例：

假设当前 \(n = 2\) ， \(m = 1\)。

两轮游戏中 Alice 分别选择了 \(t_{i}\)。

• 当 \(t_{1} < t_{2}\) 时，Bob 在第一轮一定会选择加法，那么此时第二轮就只能减法了，Alice 绝顶聪明，所以第二轮 Alice 会选择让 \(t_{2} = k\)，这样最终 \(x\) 的结果就是 \(+k - t_{1}\)。

• 当 \(t_{1} > t_{2}\) 时，Bob 在第一轮一定会选择减法，第二轮加法，Alice 会让 \(t_{2} = 0\) ，所以最终 \(x\) 答案是 \(+ t_{1} - 0 = t_{1}\)。

最终为 \(\min(t_{1}, k - t_{1})\)，在所有 \(t_{1}\) 中，答案最大是\(\frac{k}{2}\) （ \(y=x\) 和 \(y=-x+k\) 取小者，画图象可以发现是交点处最大）。

设状态 \(f_{i, j}\) 为游戏进行到第 \(i\) 轮，Bob 仍能做 \(j\) 次加法时的 \(x\) 的值，即 \(n = i, m = j\) 时的答案。

• 当 Bob 不能做加法时，Alice 想让结果变大就会让 \(t_{i} = 0\) ，这样减完最大，即 \(f_{i,0} = 0\)。

• 当 Bob 每一回合都必须做加法时（ \(m=n\) ），Alice 会让 \(t_{i} = k\) 来使结果最大，即 \(f_{i, i} = i \times k\)。

假设 Alice 选择的数是 \(t\) ，那么当 Bob 选择加法时此时的值变成 \(f_{i - 1, j - 1} + t_{i}\) ，选减法是 \(f_{i - 1, j} - t_{i}\)。

对于聪明绝顶的 Alice 来说，最优的 \(t_{i}\) 应为使得 \(\min(f_{i - 1, j - 1} + t_{i}, f_{i - 1, j} - t_{i})\) 最大的 \(t_{i}\)。

\[f_{i, j} = \max^{0\le t_{i} \le k}_{t_{i} \in \R} \{ {\min(f_{i - 1, j - 1} + t_{i}, f_{i - 1, j} - t_{i})} \} \]

其实还是可以用画图象来解决， \(f_{i, j}\) 就是 \(y=f_{i - 1, j - 1} + t_{i}\) 和 \(y=f_{i - 1, j} - t_{i}\) 取小的（自变量是 \(t_{i}\)），图像交点处最大，仍是 \(\frac{f_{i - 1, j - 1} + f_{i - 1, j}}{2}\) 这个 \(y\) 最大。

给所有数一块除以 \(k\)，在最后询问时在乘上 \(k\) ，这样可以做到 \(\text{O}(nm)\) 处理一般情况然后 \(\text{O}(1)\) 查询。\(\text{O}(Tnm) \to \text{O}(T + nm)\)。

---

CF922E Birds

题面翻译

Apart from plush toys, Imp is a huge fan of little yellow birds!

一条直线上有 \(n\) 棵树，第 \(i\) 棵树上有 \(c_i\) 只鸟。

在第 \(i\) 棵树底下召唤一只鸟的魔法代价是 \(cost_i\)。每召唤一只鸟，魔法上限会增加 \(B\)。从一棵树走到另一棵树，会增加魔法 \(X\)。一开始的魔法和魔法上限都是 \(W\)。

只能从编号为 \(1\) 的树开始，每次移动到编号为当前编号 \(+1\) 的树。

问最多能够召唤的鸟的个数。

输入格式

The first line contains four integers $ n $ , $ W $ , $ B $ , $ X $ ( $ 1<=n<=10^{{3},0<=W,B,X<=10} $ ) — the number of trees, the initial points of mana, the number of points the mana capacity increases after a bird is summoned, and the number of points restored when Imp moves from a tree to the next one.

The second line contains $ n $ integers $ c_{1},c_{2},...,c_{n} $ ( $ 0<=c_{i}<=10^{4} $ ) — where $ c_{i} $ is the number of birds living in the $ i $ -th nest. It is guaranteed that \(\sum^{n}_{i=1}{c_{i}\le 10^{4}}\) .

The third line contains $ n $ integers $ cost_{1},cost_{2},...,cost_{n} $ ( $ 0<=cost_{i}<=10^{9} $ ), where $ cost_{i} $ is the mana cost to summon a bird from the $ i $ -th nest.

输出格式

Print a single integer — the maximum number of birds Imp can summon.

样例 #1

样例输入 #1

2 12 0 4
3 4
4 2

样例输出 #1

6

样例 #2

样例输入 #2

4 1000 10 35
1 2 4 5
1000 500 250 200

样例输出 #2

5

样例 #3

样例输入 #3

2 10 7 11
2 10
6 1

样例输出 #3

11

提示

In the first sample base amount of Imp's mana is equal to $ 12 $ (with maximum capacity also equal to $ 12 $ ). After he summons two birds from the first nest, he loses $ 8 $ mana points, although his maximum capacity will not increase (since $ B=0 $ ). After this step his mana will be $ 4 $ of $ 12 $ ; during the move you will replenish $ 4 $ mana points, and hence own $ 8 $ mana out of $ 12 $ possible. Now it's optimal to take $ 4 $ birds from the second nest and spend $ 8 $ mana. The final answer will be — $ 6 $ .

In the second sample the base amount of mana is equal to $ 1000 $ . The right choice will be to simply pick all birds from the last nest. Note that Imp's mana doesn't restore while moving because it's initially full.

钱数是 \(1e9\) 不能做dp下标。

设 \(f_{i, j}\) 为走到了第 \(i\) 棵数下，已经召唤了 \(j\) 只鸟 这时剩下的魔力数。（怎么想到的？不知道）

假设在这棵树下召唤了 \(k\) 只 bird， \(f_{i, j} = \max{\{f_{i - 1, j - k} -k \times cost_{i}\} + x}\)

其中 \(f_{0, 0} = w\) 。

但是魔力有限制，所以应该加上最高限制。

\[f_{i, j} = \max{\{\min{(f_{i - 1, j - k} -k \times cost_{i} + x, w + j \times b)}\}} \]

当然，需要能召唤得起的情况下。

---

CF1616D Keep the Average High

题面翻译

给定一个长 \(n\) 的数列 \(a\)，再给定一个 \(x\)。

你需要选择其中一些数，使得对于所有长度至少为 \(2\) 的连续子串 $[l,r] $ 满足以下两个条件之一：

• 子串中至少有一个数未被选择
• \(\sum_{i=l}^ra_i\ge (r-l+1)\times x\)

求最多能选出多少个数。

多组数据。
\(1\le T\le10\)，\(1\le n\le5\times10^4\)，\(-1\times10^5\le a_i\)，\(x\le1\times10^5(1\le i\le n)\)。

输入格式

The first line of input contains one integer $ t $ ( $ 1 \leq t \leq 10 $ ): the number of test cases.

The descriptions of $ t $ test cases follow, three lines per test case.

In the first line you are given one integer $ n $ ( $ 1 \leq n \leq 50,000 $ ): the number of integers in the array.

The second line contains $ n $ integers $ a_1, a_2, \ldots, a_n $ ( $ -100,000 \leq a_i \leq 100,000 $ ).

The third line contains one integer $ x $ ( $ -100,000 \leq x \leq 100,000 $ ).

输出格式

For each test case, print one integer: the maximum number of elements that you can select.

样例 #1

样例输入 #1

4
5
1 2 3 4 5
2
10
2 4 2 4 2 4 2 4 2 4
3
3
-10 -5 -10
-8
3
9 9 -3
5

样例输出 #1

4
8
2
2

提示

In the first example, one valid way to select the elements is $ [\underline{1}, 2, \underline{3}, \underline{4}, \underline{5}] $ . All subsegments satisfy at least one of the criteria. For example, for the subsegment $ l = 1 $ , $ r = 2 $ we have that the element $ 2 $ is not selected, satisfying the first criterion. For the subsegment $ l = 3 $ , $ r = 5 $ we have $ 3 + 4 + 5 = 12 \ge 2 \cdot 3 $ , satisfying the second criterion.

We can't select all elements, because in this case for $ l = 1 $ , $ r = 2 $ all elements are selected and we have $ a_1 + a_2 = 3 < 2 \cdot 2 $ . Thus, the maximum number of selected elements is $ 4 $ .

In the second example, one valid solution is $ [\underline{2}, \underline{4}, 2, \underline{4}, \underline{2}, \underline{4}, 2, \underline{4}, \underline{2}, \underline{4}] $ .

In the third example, one valid solution is $ [\underline{-10}, -5, \underline{-10}] $ .

In the fourth example, one valid solution is $ [\underline{9}, \underline{9}, -3] $ .

首先：

\(\sum^{r}_{i=l}{a_{i}} \ge (r - l + 1) \times x \implies \sum^{r}_{i=l}{a_{i}} - \sum^{r}_{i=l}{x} \ge 0 \implies \sum^{r}_{i=l}{(a_{i} - x)} \ge 0\)

然后 题解告诉我们 只需要长度为 \(2\) 和长度为 \(3\) 的子串满足条件，所有的子串就会满足条件，至于为什么是这样的？ 题解说 "不难发现"。

根据结论 我们就可以判断当 \(a_{i} + a_{i - 1} + a_{i - 2} < 0\) 或 \(a_{i} + a_{i - 1} < 0\) 时就不可以被选。

诶学校OJ的CF bot也死了
剩下的都是黑题紫题了...

11.24

学校OJ的CF bot 还没活

今日是字符串，还是一堆CF的题，看见了几个B题，一个A题（

原来CF还有 H 题，长见识了。

Paranoid String

题面翻译

对一个字符串，有以下两种操作：

• 将子串 01 替换为 1

• 将子串 10 替换为 0

\(t\) 组数据，每组给定一个长度为 \(n\) 的 01 串 \(S\) 。求 \(S\) 的子串个数，满足经过若干次操作，可将该子串长度变为 \(1\) 。

\(1\le t\le 1000,1\le n\le 2\times 10^5,\sum n\le 2\times 10^5\)

输入格式

The first line contains an integer $ t $ ( $ 1 \le t \le 1000 $ ) — the number of test cases. The description of test cases follows.

The first line of each test case contains a single integer $ n $ ( $ 1 \le n \le 2 \cdot 10^5 $ ) — the size of $ S $ .

The second line of each test case contains a binary string $ S $ of $ n $ characters $ S_1S_2 \ldots S_n $ . ( $ S_i = $ 0 or $ S_i = $ 1 for each $ 1 \le i \le n $ )

It is guaranteed that the sum of $ n $ over all test cases doesn't exceed $ 2 \cdot 10^5 $ .

输出格式

For each test case, output the number of pairs of integers $ (l, r) $ $ 1 \le l \le r \le n $ such that $ S[l \ldots r] $ (the substring of $ S $ from $ l $ to $ r $ ) is a paranoid string.

样例 #1

样例输入 #1

5
1
1
2
01
3
100
4
1001
5
11111

样例输出 #1

1
3
4
8
5

提示

In the first sample, $ S $ already has length $ 1 $ and doesn't need any operations.

In the second sample, all substrings of $ S $ are paranoid. For the entire string, it's enough to perform the first operation.

In the third sample, all substrings of $ S $ are paranoid except $ [S_2S_3] $ , because we can't perform any operations on it, and $ [S_1S_2S_3] $ (the entire string).

题目中给出的两种操作的意思就是 如果相邻的两个字符不相等就可以毙掉左边的那个字符，否则就只能等右边有没有和他不相等的来毙掉他自己

那么最终一定会变成一串相同的字符组成的串。

计算每一位对答案的贡献：

• 若 \(s_{i} = s_{i - 1}\) 则此时 \([1, i]\) 范围内组成的字串（以 \(i\) 做结尾）一点都毙不动，所以这时满足条件的字串只能本来就长度为 \(1\) ，以 \(i\) 位置结尾的长度为一的串只有 \(1\) 个。

• 若 \(s_{i} \ne s_{i - 1}\) 则此时 \([1, i]\) 范围内组成的字串（以 \(i\) 做结尾）的串一定都可以被毙完（就算左边有和 \(s_{i}\) 相同的字符，也会因为 \(s_{i - 1}\) 和他不同而被一路毙过去），那么字串就有 \(i\) 个。

ans = 1;
for (int i = 1 ; i < s.size() ; i ++)
{
    ans += s[i - 1] == s[i] ? 1 : (i + 1);
}

KMP 不行。。。。

使用哈希跑过 Passworld

Merlin 要求学树形 DP，遂从之。

[NOI2002] 贪吃的九头龙

题目背景

传说中的九头龙是一种特别贪吃的动物。虽然名字叫“九头龙”，但这只是 说它出生的时候有九个头，而在成长的过程中，它有时会长出很多的新头，头的 总数会远大于九，当然也会有旧头因衰老而自己脱落。

题目描述

有一天，有 \(M\) 个脑袋的九头龙看到一棵长有 \(N\) 个果子的果树，喜出望外，恨不得一口把它全部吃掉。可是必须照顾到每个头，因此它需要把 \(N\) 个果子分成 \(M\) 组，每组至少有一个果子，让每个头吃一组。

这 \(M\) 个脑袋中有一个最大，称为“大头”，是众头之首，它要吃掉恰好 \(K\) 个果子，而且 \(K\) 个果子中理所当然地应该包括唯一的一个最大的果子。果子由 \(N-1\) 根树枝连接起来，由于果树是一个整体，因此可以从任意一个果子出发沿着树枝“走到”任何一个其他的果子。

对于每段树枝，如果它所连接的两个果子需要由不同的头来吃掉，那么两个头会共同把树枝弄断而把果子分开；如果这两个果子是由同一个头来吃掉，那么这个头会懒得把它弄断而直接把果子连同树枝一起吃掉。当然，吃树枝并不是很舒服的，因此每段树枝都有一个吃下去的“难受值”，而九头龙的难受值就是所有头吃掉的树枝的“难受值”之和。

九头龙希望它的“难受值”尽量小，你能帮它算算吗？

例如图 \(1\) 所示的例子中，果树包含 \(8\) 个果子，\(7\) 段树枝，各段树枝的“难受值”标记在了树枝的旁边。九头龙有两个脑袋，大头需要吃掉 \(4\) 个果子，其中必须包含最大的果子。即 \(N=8\)，\(M=2\)，\(K=4\)：

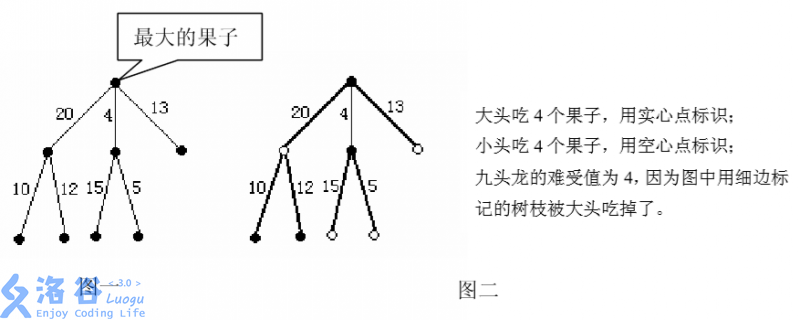
图一描述了果树的形态，图二描述了最优策略。

输入格式

输入的第 \(1\) 行包含三个整数 \(N\ (1 \le N \le 300)\)，\(M(2 \le M \le N)\)，\(K(1 \le K \le N)\)。\(N\) 个果子依次编号 \(1,2, \cdots N\)，且最大的果子的编号总是 \(1\)。

第 \(2\) 行到第 \(N\) 行描述了果树的形态，每行包含三个整数 \(a\ (1 \le a \le N), b\ (1 \le b \le N), c\ (0 \le c \le 10^5)\)，表示存在一段难受值为 \(c\) 的树枝连接果子 \(a\) 和果子 \(b\)。

输出格式

输出仅有一行，包含一个整数，表示在满足“大头”的要求 的前提下，九头龙的难受值的最小值。如果无法满足要求，输出 \(-1\)。

样例 #1

样例输入 #1

8 2 4 
1 2 20 
1 3 4 
1 4 13 
2 5 10 
2 6 12 
3 7 15 
3 8 5

样例输出 #1

4

提示

该样例对应于题目描述中的例子。

设计状态的时候需要考虑到 大头 的限制：

• 大头 必须要吃 \(1\) 号节点。

• 大头 必须 恰好吃掉 \(k\) 个节点。

所以我们设 \(f_{i, j, 0/1}\) 表示第 \(i\) 号节点， 他和他的儿子们一共有 \(j\) 个节点是被 大头 吃掉的，并且 \(0/1\) 表示 \(i\) 是否是大头吃掉的。（值为最小“难受值”）

根据定义，我们要求的最终答案为 \(f_{1, k, 1}\) 。

\(\forall\) 节点 \(u\) 我们要把 \(\forall j \in [0, k], f_{u, j, 0/1}\) 都全部更新才算是转移完状态。如果现在有 \(3\) 及以上个头存在，那么就算某一条边两端没有一个点被 大头 吃掉，那么也一定可以分配给其他头吃掉使得避免这个树枝被吃掉。但是如果只有 \(2\) 个头并且这时候这个树枝两边都没有被 大头 给吃掉，那么这个树枝就不可避免地被吃掉了。所以 \(m = 2\) 时是特殊情况。

• 大头 不吃 \(u\) 时 \(f_{u, j, 0} = \min^{j}_{t = 0} \{ f_{v, t, 0} + f_{u, j - t, 0} + [m == 2] \times w, f_{v, t, 1} + f_{u, j - t, 0}\}\) （讨论 大头 吃 \(v\) 与否的情况）

• 大头 吃 \(u\) 时 \(f_{u, j, 1} = \min^{j}_{t = 0} \{ f_{v, t, 1} + f_{u, j - t, 1} + w, f_{v, t, 0} + f_{u, j - t, 1}\}\) （讨论 大头 吃 \(v\) 与否的情况）

（ \(u, v, w\) 是 \(u \to^{w} v\) ）

for (int j = 0 ; j <= k ; j ++)
{
    for (int t = 0 ; t <= j ; t ++)
    {
        f[u][j][0] = min(f[u][j][0], min(f[v][t][0] + f[u][j - t][0] + (m == 2) * w, f[v][t][1] + f[u][j - t][0]));
        f[u][j][1] = min(f[u][j][1], min(f[v][t][1] + f[u][j - t][1] + w, f[v][t][0] + f[u][j - t][1]));
    }
}

这个转移代码挂掉的原因是在转移的时候被修改了（

所以还要在修改之前先记录，不然会乱掉。每次记录 \(f_{u}\) 让 \(temp\) 在开始转移之前记录 \(f_{u}\) 的初始值，转移的时候用 \(temp\) 而非 \(f_{u, j - t}\) 。

无解情况：

题目里说的是每一个头都至少要吃掉 \(1\) 个节点，所以当 大头 吃完以后剩下的不够分了就报告无解。 \(n - k < m - 1\)

---

• tips for fixing computer system crashes.

• The computer that we use at the moment often crash. Exactly.

• JET ENGINE.

• a pipe dream. it means the "Just image".

• calm -> The weather was finie and the lake was calm. On the ANDONG's planet, tons of waves in the lakes and rivers but no wind.

---

11.25

OJ的 CF 波特还没复活

[COCI2014-2015#1] Kamp

题目描述

一颗树 \(n\) 个点，\(n-1\) 条边，经过每条边都要花费一定的时间，任意两个点都是联通的。

有 \(K\) 个人（分布在 \(K\) 个不同的点）要集中到一个点举行聚会。

聚会结束后需要一辆车从举行聚会的这点出发，把这 \(K\) 个人分别送回去。

请你回答，对于 \(i=1 \sim n\) ，如果在第 \(i\) 个点举行聚会，司机最少需要多少时间把 \(K\) 个人都送回家。

输入格式

第一行两个整数 \(n,K\) 。

接下来 \(n-1\) 行，每行三个数 \(x,y,z\) 表示 \(x\) 到 \(y\) 之间有一条需要花费 \(z\) 时间的边。

接下来 \(K\) 行，每行一个数，表示 \(K\) 个人的分布。

输出格式

输出 \(n\) 个数。

第 \(i\) 行的数表示：如果在第 \(i\) 个点举行聚会，司机需要的最少时间。

样例 #1

样例输入 #1

7 2
1 2 4
1 3 1
2 5 1
2 4 2
4 7 3
4 6 2
3
7

样例输出 #1

11
15
10
13
16
15
10

样例 #2

样例输入 #2

5 2
2 5 1
2 4 1
1 2 2
1 3 2
4
5

样例输出 #2

5
3
7
2
2

提示

数据规模与约定

• 对于 \(50\%\) 的数据，保证 \(n\le 2\times 10^3\)。
• 对于 \(100\%\) 的数据， \(1 \le k \le n \leq 5\times 10^5\)，\(1 \le x,y \le n\)，\(1 \le z \le 10^8\) 。

在 \(i\) 号点举行聚会时，令 \(i\) 为树根，求把所有 \(K\) 个人送回家的最短时间。

我们维护子树内的信息，令 \(g_{u}\) 为以 \(u\) 为根的子树中从 \(u\) 开始把在这个子树内的所有人送回家并返回 \(u\) 节点所需要的最短时间。 \(sz_{u}\) 为家在以 \(u\) 为根的子树中的人数。逆序从 \(u\) 可以一步去到的点 \(v\) 计算 \(g_{u}\) 可以用 所有 \(g_{v} + 2 \times w_{u\to v}\)。（从儿子算到父亲）

\[g_u = \sum_{u\to v}^{sz_{v} \ne 0}(g_{v} + 2\times w_{u\to v}) \]

然后我们发现这样算的话我们必须回到一开始的 \(i\) 号点，题目意思是不用回来，所以我们还要减掉一个距离出发点最长的人的家的距离。并且维护一个次长距离。（暂且叫他们最长链和次长链）

\(len_{u}\) 为从 \(u\) 出发的最长链， \(slen_{u}\) 为次长链， \(id_{u}\) 为从 \(u\) 开始的最长链第一个经过的结点（判断是儿子节点还是父亲节点用的）。

处理子树内的信息的代码：

void dfs(int u, int fa)
{
    if (pos[u] == true) // u点是否有人住。
    {
        sz[u] = 1;
    }
    for (auto &it : G[u])
    {
        int v = it.first, w = it.second;
        if (v == fa)
        {
            continue;
        }
        dfs(v, u);
        if (sz[v] >= 1) // 没人更新个集贸
        {
            g[u] = g[v] + 2 * w;
            if (len[v] + w >= len[u]) // 都更新
            {
                slen[u] = len[u];
                len[u] = len[v] + w;
                id[u] = v;
            }
            else if (len[v] + w > slen[u]) // 只更新次长链
            {
                slen[u] = len[v] + w;
            }
        }
        sz[u] += sz[v];
    }
}

有了这些信息以后，我们就可以把眼光放到整棵树上了。

设 \(f_{u}\) 为在整棵树上从 \(u\) 开始送完人 最后回到 \(u\) 点所需要的最短距离。

分类讨论qwq

1. \(sz_{v} = 0\) \(v\) 的子树中没有人家，显然可以直接给这些子树节点们扩散 \(f_{v} = f_{u} + 2 \times w_{u \to v}\) 。（只是白白多走的路，从 \(v\) 到 \(u\) 之后走的路就和 \(f_{u}\) 一样了）

2. \(sz_{v} = K\) ，人家全部在 \(v\) 的子树下，和 \(v\) 的父亲 \(u\) 没啥关系了，那么 眼光又可以缩回来了， \(f_{v} = g_{v}\) 。

3. 其他情况 \(f_{v} = f_{u}\) 。（貌似）

还要更新全局视角下的 \(len\) 和 \(slen\) 。情况和上面的分的一样。

1. 仍然是直接从 \(v\) 直走到 \(u\) 就行了 \(len_{v} = len_{u} + w_{u \to v}\) 。

2. 这次不用动了， 定义都没变

3. 这次不能直接转移了，还要继续分类。（都是从前往后只能满足一个。 人话：if 和 else if）

   1. \(len_{u} + w_{u \to v} \ge len_{v}\) 且 \(id_{u} \ne v\) （因为 \(id_{u} = v\) 的时候不能更新）直接更新。

   2. \(len_{u} + w_{u \to v} \ge len_{v}\) 且 \(id_{u} = v\) 如上，不能更新，不然就不是链了。

   3. 还要考虑次长链 \(slen_{u} + w_{u \to v} \ge len_{v}\) 可以用 \(u\) 的次长链更新 \(v\) 。

   4. \(len_{u} + w_{u \to v} \ge slen_{v}\) 且 \(id_{u} \ne v\) 用 \(u\) 最长链更新 \(v\) 次长链。

   5. \(len_{u} + w_{u \to v} \ge slen_{v}\) 且 \(id_{u} = v\) 同 第二种情况。

   6. \(slen_{u} + w_{u \to v} \ge slen_{v}\) 最显然的一集。

具体怎么更新看代码。

void dfs2(int u, int fa)
{
    for (auto &it : G[u])
    {
        int v = it.first, w = it.second;
        if (v == fa)
        {
            continue;
        }
        if (sz[v] == 0) // 情况 1
        {
            f[v] = f[u] + 2 * w;
        }
        else if (sz[v] == k) // 情况 2
        {
            f[v] = g[v];
        }
        else // 最复杂的 3
        {
            f[v] = f[u];
            if (id[u] != v and len[v] < len[u] + w)
            {
                slen[v] = len[v];
                len[v] = len[u] + w;
                id[v] = u;
            }
            else if (len[v] < slen[u] + w)
            {
                slen[v] = len[v];
                len[v] = slen[u] + w;
                id[v] = 1;
            }
            else if (slen[v] < len[u] + w and id[u] != v)
            {
                slen[v] = len[u] + w;
            }
            else if (slen[v] < slen[u] + w)
            {
                slen[v] = slen[u] + w;
            }
        }
        dfs2(v, u);
    }
}

草过不了样例。。。

---

另外：
2024/11/25 星期一
大约 9:05 a.m. ：学校所有OJ一起爆炸了。（Edge说返回了错误的证书和凭据，我们在数据交换之前就中断了一切连接，Google说"你的时钟似乎走快了"）祭

9:20 a.m. ：草，这么快就活了？

---

ST表一定要记住（

for (int i = 2 ; i <= n ; i ++)
{
    lg[i] = lg[i >> 1] + 1;
}

先求出每个要用的 \(\log_{2}{x}\) 的值。

\(f_{i, j}\) 表示 从 \(i\) 到后面数 \(2^{j}\) 个数里面的最大值。

因为区间最值可以直接合并。

for (int j = 1 ; j <= lg[n] ; j ++)
{
    for (int i = 1 ; i <= n - (1 << j) + 1 ; i ++)
    {
        f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
    }
}

\(k = \log_{2}{(R - L + 1)}\), 查询是 \(\max{(f_{L, k}, f_{R - (1 << k) + 1, k})}\)

Merlin 学习 笛卡尔树：

笛卡尔树

定义

笛卡尔树是二叉树的一种，每个节点有两个关键字，分别满足堆和二叉搜索树的性质。一个序列上的笛卡尔树的两个关键字就是值和下标。

建树

通过定义我们可以得到一个建树方法：

对序列 \([l, r]\) 建立笛卡尔树（比如说最小值的），先找到 \([l, r]\) 的最小值（序列中的位置为 \(p\) ）当作根，然后对序列 \([l, p - 1]\) 和 \([p + 1, r]\) 进行建树，并且 \([l, p - 1]\) 部分是 \(p\) 的左子树， \([p + 1, r]\) 部分是 \(p\) 的右子树。

这样建出来的树满足一个节点的左 / 右子树的下标只能在这个节点的下标的左 / 右。

用栈构建笛卡尔树

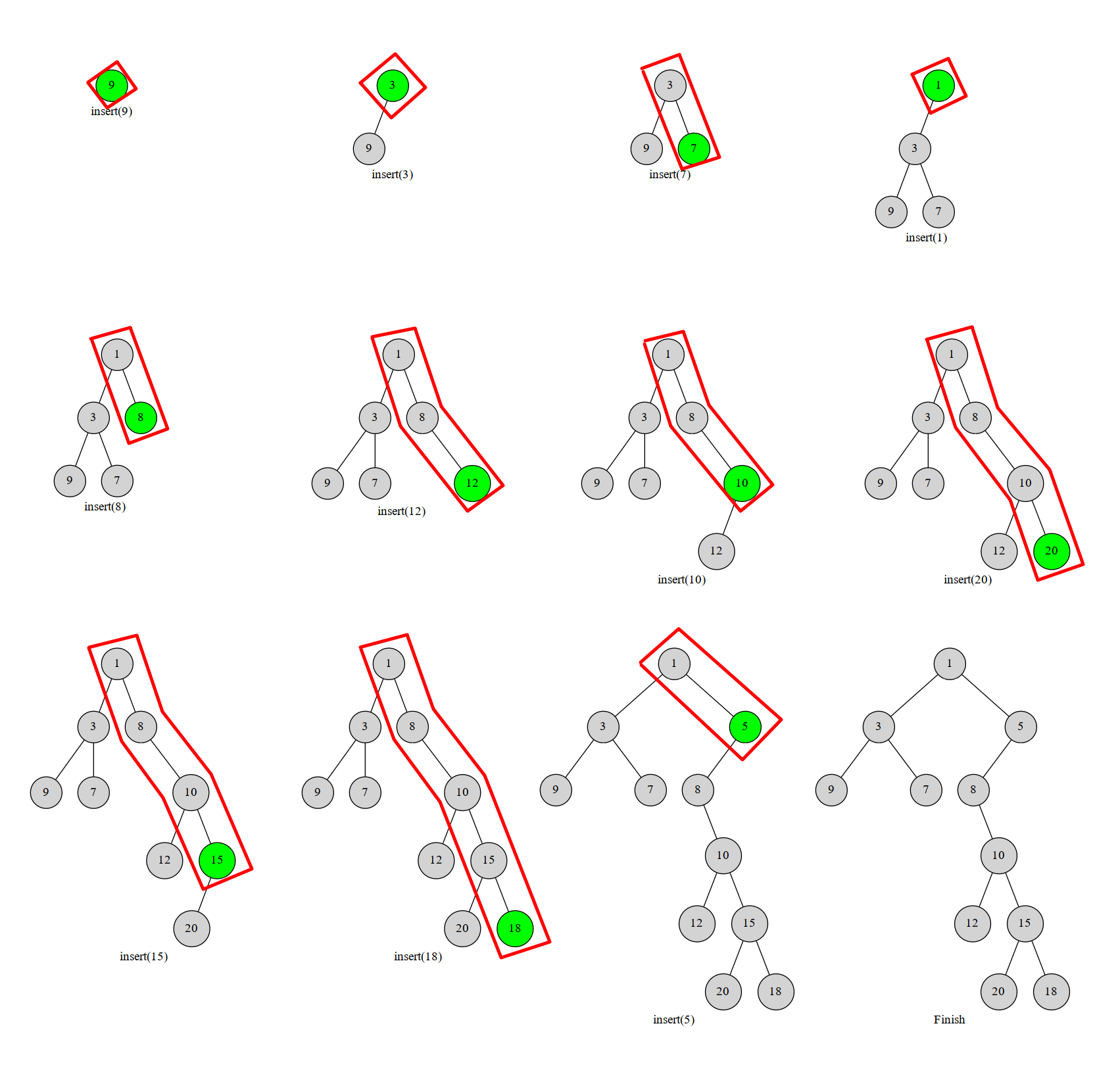
我们考虑将元素按下标顺序依次插入到当前的笛卡尔树中。那么每次我们插入的元素必然在这棵树的右链（右链：即从根节点一直往右子树走，经过的节点形成的链）的末端。

从下往上比较右链节点与当前节点 \(u\) 的值，如果找到一个右链上的节点 \(x\) 满足其值小于 \(u\) 上的值，就把 \(u\) 接到 \(x\) 的右儿子上，把 \(x\) 本来的右子树变成 \(u\) 的左子树。OI-wiki 给出了一个过程图：

图中红框部分就是我们始终维护的右链：

显然每个数最多进出右链一次（或者说每个点在右链中存在的是一段连续的时间）。这个过程可以用栈维护，栈中维护当前笛卡尔树的右链上的节点。一个点不在右链上了就把它弹掉。这样每个点最多进出一次，复杂度 \(O(n)\)

那感觉这个代码应该很难写吧

int build(int l, int r)
{
    for (int i = l ; i <= r ; i ++)
    {
        int k = top;
        while (k > 0 and a[stk[k]] > a[i])
        {
            k --;
        }
        if (k)
        {
            rs[stk[k]] = i;
        }
        if (k < top)
        {
            ls[i] = stk[k + 1];
        }
        stk[++ k] = i;
        top = k;
    }
    return stk[1]; // 最小的就是根，根就是最小的。
}

int query(int root, int l, int r) // 随机数据下 树高期望为 logn 所以随机数据下复杂度是可以的，但是这仍然会被卡成 O(n) 应该配合其他稳定复杂度求 LCA 的算法食用。
{
    while (root < l or root > r)
    {
        if (root < l)
        {
            root = rs[root];
        }
        else
        {
            root = ls[root];
        }
    }
    return root;
}

这是一个返回最小值的代码，如果需要查找最大值可以给数据全部变成负的（

性质

笛卡尔树有一个美妙的性质，对于 \([l, r]\) 的最值就是下标为 \(l\) 和 \(r\) 的节点的 LCA 对应的值。

被骗力

Merlin 说 笛卡尔树 可以弥补 ST表 占空间的缺点。

但是 \(O(1)\) 查询 的优点也被弥补了啊喂！

需要配合树剖求LCA使用？

---

14:54 ：
HZOI 的 CF 波特又活了。

---

万径人踪灭

题目描述

就是要在一个只含 a、b 的字符串中选取一个子序列，使得:

1. 位置和字符都关于某条对称轴对称。
2. 不能是连续的一段。

以 \(s = \texttt{"abaaaaabbabbabaa"}\) 为例。如果我们用符号 \([a_1, a_2,…,a_k]\) 表示一个序列，那么 \([1,4]\) 就是一个合法的序列 \(x\)，\([5,8,10,12,15]\) 也是，\([4,5,8,9,10,11,12,15,16]\) 也是。但是 \([1,2]\) 不满足 VFleaKing 第一个希望和第三个希望，所以不是。\([1,2,4]\) 不满足第二个希望，所以不是。\([9,10,11]\) 不满足第三个希望，所以不是。

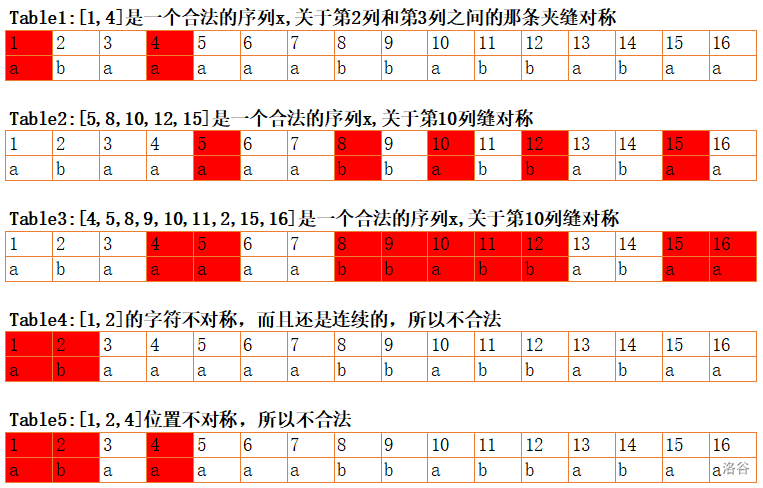
给你字符串 \(s\)，现在 VFleaKing 想知道，有多少个合法的 \(x\)。答案可能很大，VFleaKing 想知道对 \(1000000007\) 取模的值。

输入格式

一行，一个只包含 a、b 的两种字符的字符串。

输出格式

一行，一个非负整数表示问题的答案。

样例 #1

样例输入 #1

abaabaa

样例输出 #1

14

样例 #2

样例输入 #2

aaabbbaaa

样例输出 #2

44

样例 #3

样例输入 #3

aaaaaaaa

样例输出 #3

53

提示

样例解释

样例解释 1

\(14\) 个方案分别是：

• \([1,3]\)，\([1,4]\)，\([2,5]\)，\([1,6]\)，\([3,6]\)，\([4,6]\)，\([1,7]\)，\([3,7]\)，\([4,7]\)；
• \([1,4,7]\)，\([3,5,7]\)；
• \([1,3,4,6]\)，\([1,2,5,6]\)，\([3,4,6,7]\)。

数据范围

• 其中 \(10\%\) 的数据，字符串仅包含字母 a 或字母 b。
• 另有 \(20\%\) 的数据，\(n\le 1000\)。
• 另有 \(20\%\) 的数据，要么 a 的个数不超过 \(10\)，要么 a 的个数不超过 \(10\)。
• 另有 \(10\%\) 的数据，\(n\le 10000\)。
• 对于 \(100\%\) 的数据，\(n \le 100000\)。

"不连续的位置对称的回文子序列数" 等于 "位置对称的回文子序列数" - "回文子串数"

现有 \(x = 0\) ，当 \(S_{i - j} = S_{i + j} ,(1 \le j \le i - 1)\) 时， \(x + 1\) 。算上中心，一共是 \(x + 1\) 个 "选 / 不选"，故刨除掉一个也不选的情况一共是 \(2^{x + 1} - 1\) 种情况。

但是，还有对称轴在夹缝里的情况，这时答案应为 \(2^x - 1\) ，因为这次没有对称中心那一个了。

计算 \(x\) 的值：

不会，寄，看题解，FFT， \(6\)

11.26

嗯呕唉屁 膜你塞。

垫底，不会。

T2 正解最后整了个

Merlin 企图学

11.27

成功切掉 T1 。

不是？这也能死？

T2 T3 T4 暴力均有挂分。

11.28

成功 切掉 T1。

有 \(n\) 堆果子，分别有 \(a_{1}, a_{2}, ⋯ , a_{n}\) 个果子。一次合并分为有顺序的 \(n - 1\) 步，每一步选择两堆果子，合并成一堆。

定义一次合并的权值为每一步被合并的两堆果子数量之积的和。求出每一种合并方法的权值之和对 \(998244353\) 取模的结果。

两种合并方式不同当且仅当有一步被合并的两堆不同。即使有两堆的果子数量相同，我们仍然把它们视为不同的两堆。

求所有合并方法权值之和（对 \(998244353\) 取模）。

赛时：

耶，有 \(a_{i} = 1\) 的全是 \(1\) 的部分分。

发现对于一种选择，最终贡献一定是 这些数两两相乘的和，值全部为 \(1\) 时，一种选择的贡献为 \(n \choose 2\)

一共有多少种选择方案？

• 第一步：显然可以有 \(n \choose 2\) 种
• 第二部：少了一堆，就是 \({n - 1} \choose 2\) 种。
• 那么剩下的同理，一直到剩两个。

根据乘法原理一共是

\[\displaystyle\prod\limits_{i = 2}^{n}{i \choose 2} \]

此物瞎递推一下就行。

所以答案为

\[(\displaystyle\prod\limits_{i = 2}^{n}{i \choose 2}) \times {n \choose 2} \]

人类智慧告诉我每次无论怎么选合并完贡献都是一样的（

这是瓶颈来到了求单次贡献，所有数两两相乘的和。

\[S=\{ a_{i} \times a_{j} | 1 \le i, j \le n , i \ne j \} \]

那么，「暴力，准备就绪」。

运用人类智慧，发现当：令 \(S_2 = \sum_{i}{a_i}\) 时， \(S_{2} ^ {2}\) 结果中含有的一次多项式 正好 包含 \(S\) 中要求的所有多项式，只不过系数是 \(2\) ，并且多出一些二次项。

那我们考虑令 \(S_{3} = \sum_{i}{a_{i}^{2}}\) ，则 \(S_2 - S_3 = 2 \times S\)， \(S\) 就可以求出了。

这样我们就可以 \(O(n \log n)\) 求出结果了，一看 \(N \le 10^5\) 果断写完开润（