汉诺塔问题

原理

相传在古印度圣庙中，有一种被称为汉诺塔(Hanoi)的游戏。该游戏是在一块铜板装置上，有三根杆(编号a、b、c)，在A杆自下而上、由大到小按顺序放置n个金盘(如图)。

游戏的目标：把A杆上的金盘全部移到c杆上，并仍保持原有顺序叠好。

操作规则：每次只能移动一个盘子，并且在移动过程中三根杆上都始终保持大盘在下，小盘在上，操作过程中盘子可以置于a、b、c任一杆上。

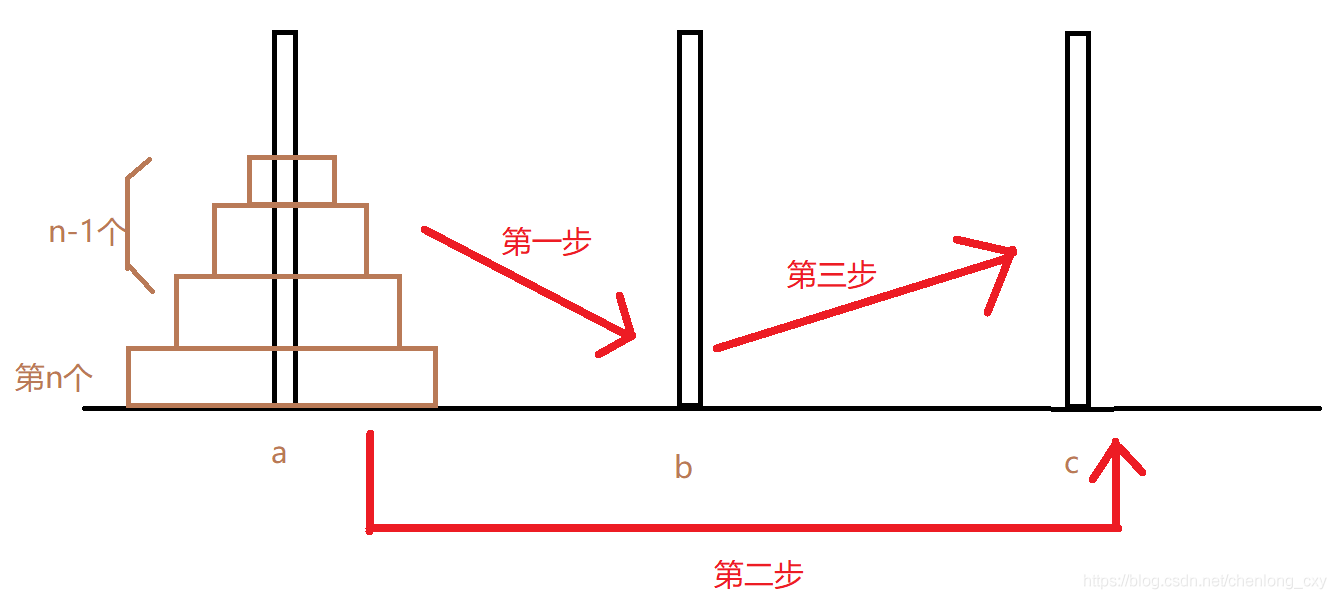
步骤

1. 将n-1个盘子通过c移动到b，n-1个盘子看作是一个整体
2. 将第n个盘子从a移动到c
3. 将n-1个盘子从b通过a移动到c

代码

递归思想

def hanno(n, a, b, c):
    if n > 0:
	hanno(n - 1,  a, c, b)
	print("将第 %s 个盘子从 %s 移动到 %s" % (n, a, c))
	hanno(n - 1, b, a, c)

hanno(3, "A", "B", "C")

输出结果

将第 1 个盘子从 A 移动到 C
将第 2 个盘子从 A 移动到 B
将第 1 个盘子从 C 移动到 B
将第 3 个盘子从 A 移动到 C
将第 1 个盘子从 B 移动到 A
将第 2 个盘子从 B 移动到 C
将第 1 个盘子从 A 移动到 C