算法与数据结构
稀疏数组
线性结构:
○ 线性结构作为最常用的数据结构,其特点是数据元素之间存在一对一的线性关系
○ 线性结构有两种不同的存储结构,即顺序存储结构和链式存储结构。顺序存储的线性表称为顺序表,顺序表中的存储元素是连续的
○ 链式存储的线性表称为链表,链表中的存储元素不一定是连续的,元素节点中存放数据元素以及相邻元素的地址信息
○ 线性结构常见的有:数组、队列、链表和栈
非线性结构:
○ 非线性结构包括:二维数组,多维数组,广义表,树结构,图结构
稀疏数组---Sparsearray:
基本介绍:
当一个数组中大部分元素为0,或者为同一个值的数组时,可以使用稀疏数组来保存该数组。
稀疏数组的处理方法是:
记录数组一共有几行几列,有多少个不同的值
把具有不同值的元素的行列及值记录在一个小规模的数组中,从而缩小程序的规模
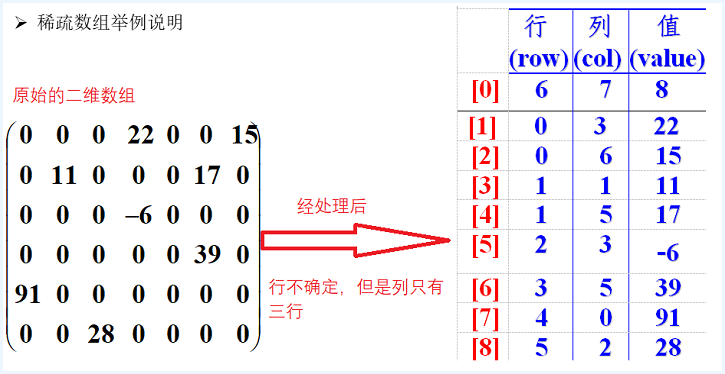
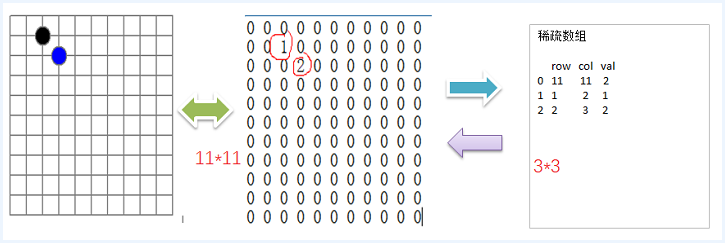
应用实例
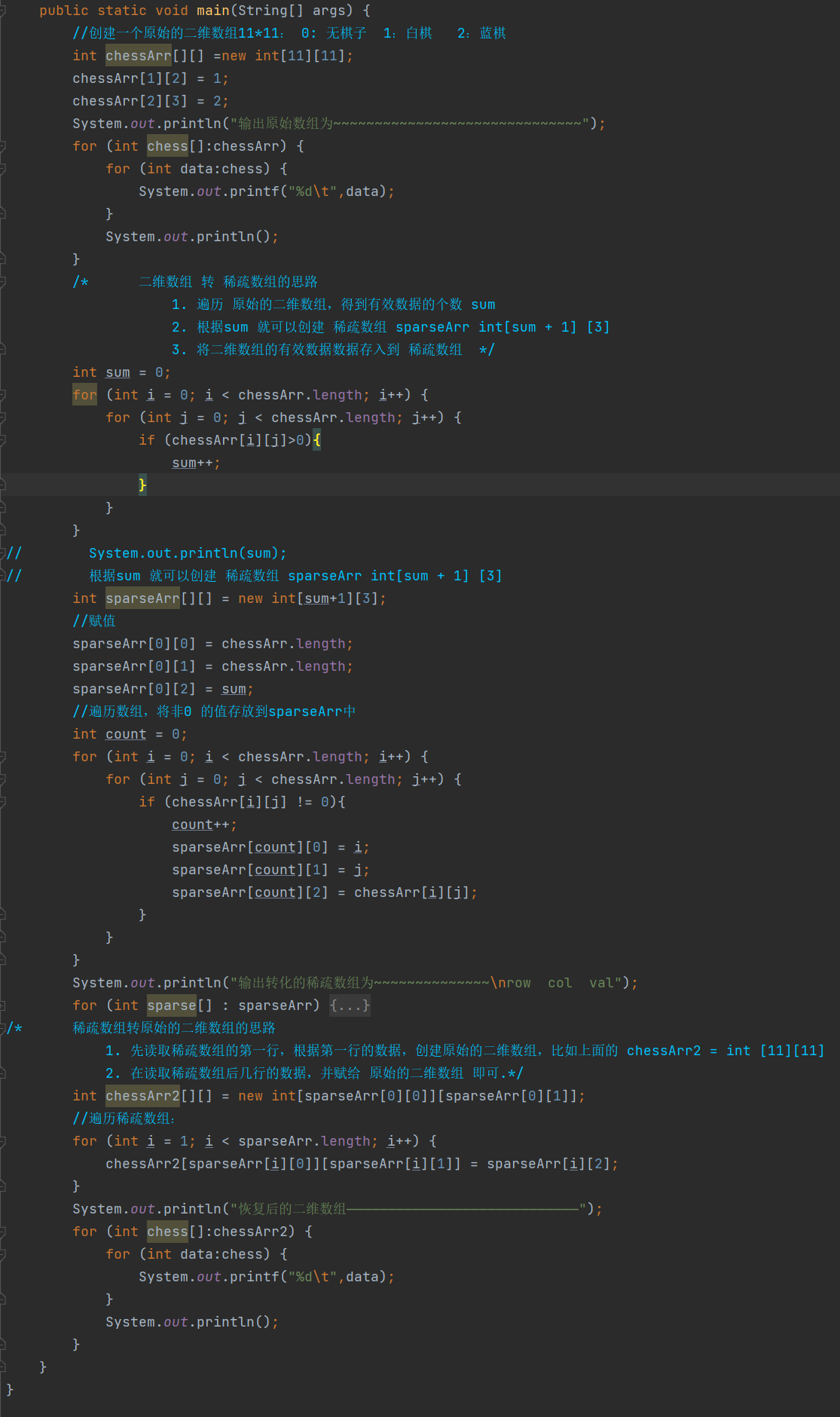
二维数组 转 稀疏数组的思路
1. 遍历 原始的二维数组,得到有效数据的个数 sum
2. 根据sum 就可以创建 稀疏数组 sparseArr int[sum + 1] [3]
3. 将二维数组的有效数据数据存入到 稀疏数组
稀疏数组转原始的二维数组的思路
1. 先读取稀疏数组的第一行,根据第一行的数据,创建原始的二维数组,比如上面的 chessArr2 = int [11][11]
2. 在读取稀疏数组后几行的数据,并赋给 原始的二维数组 即可.
代码实例
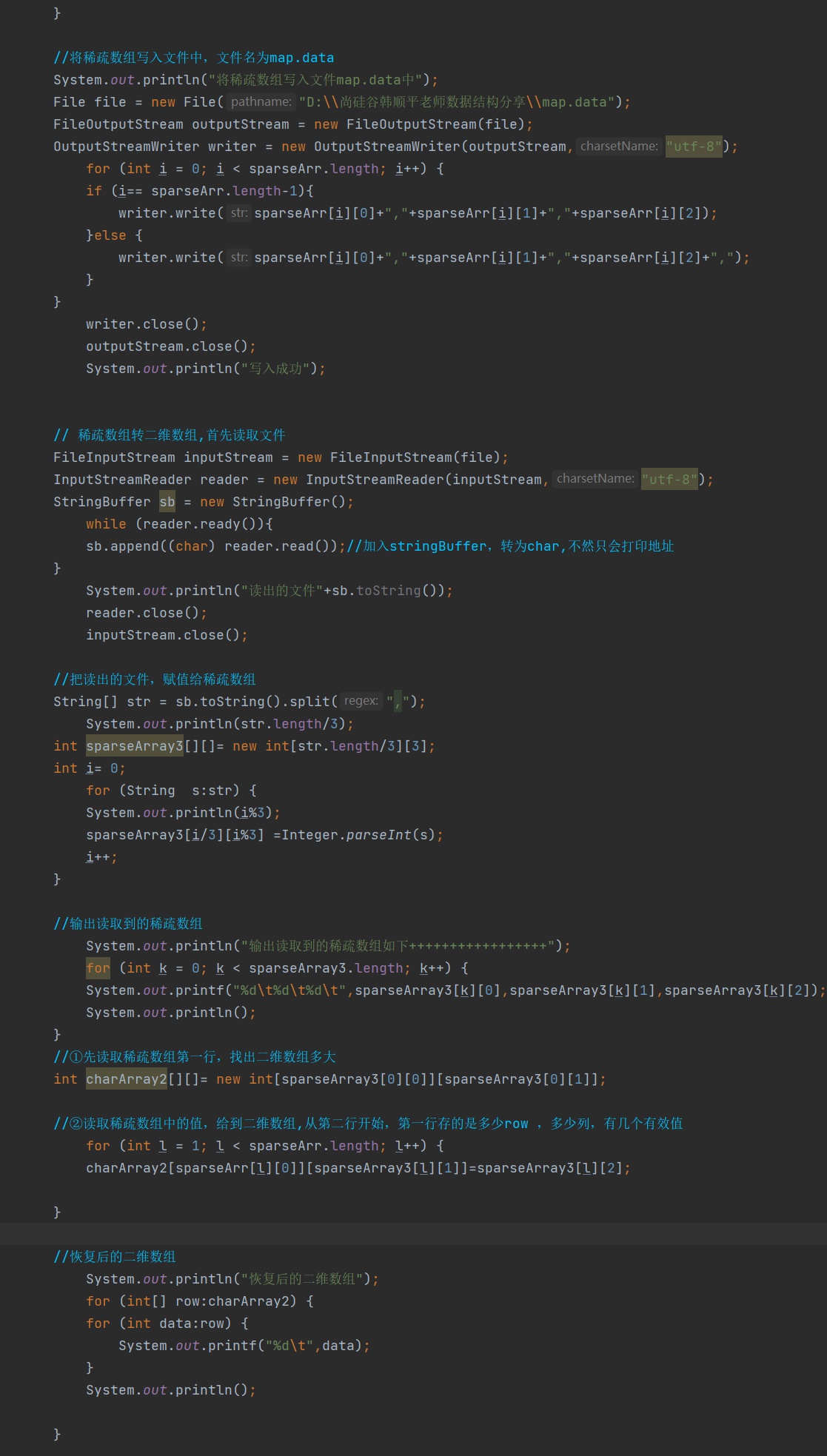
队列
队列的介绍
○ 队列是一个有序列表,可以用数组或是链表来实现。
○ 遵循先入先出的原则。即:先存入队列的数据,要先取出。后存入的要后取出
数组模拟队列:
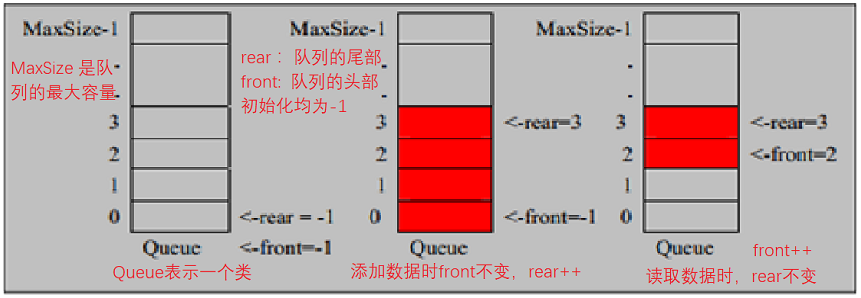
因为队列的输出、输入是分别从前后端来处理,因此需要两个变量 front及 rear分别记录队列前后端的下标,front 会随着数据输出而改变,而 rear则是随着数据输入而改变
缺点-------没有做成环形队列,数组添加一次,之后就不能在往里面添加了
修改------只需要把改队列改成环形对列,这样就可以循环反复往里面添加数据了
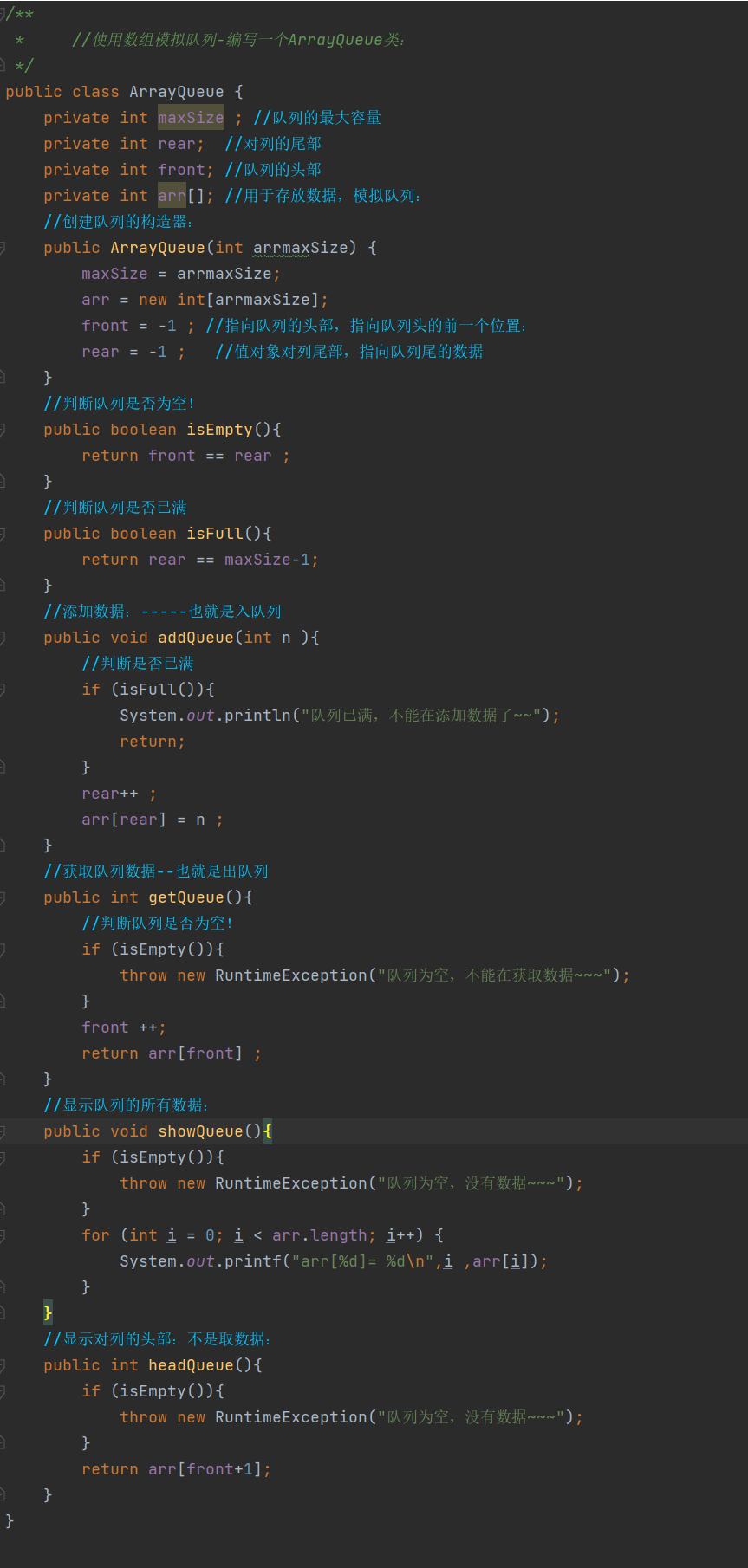
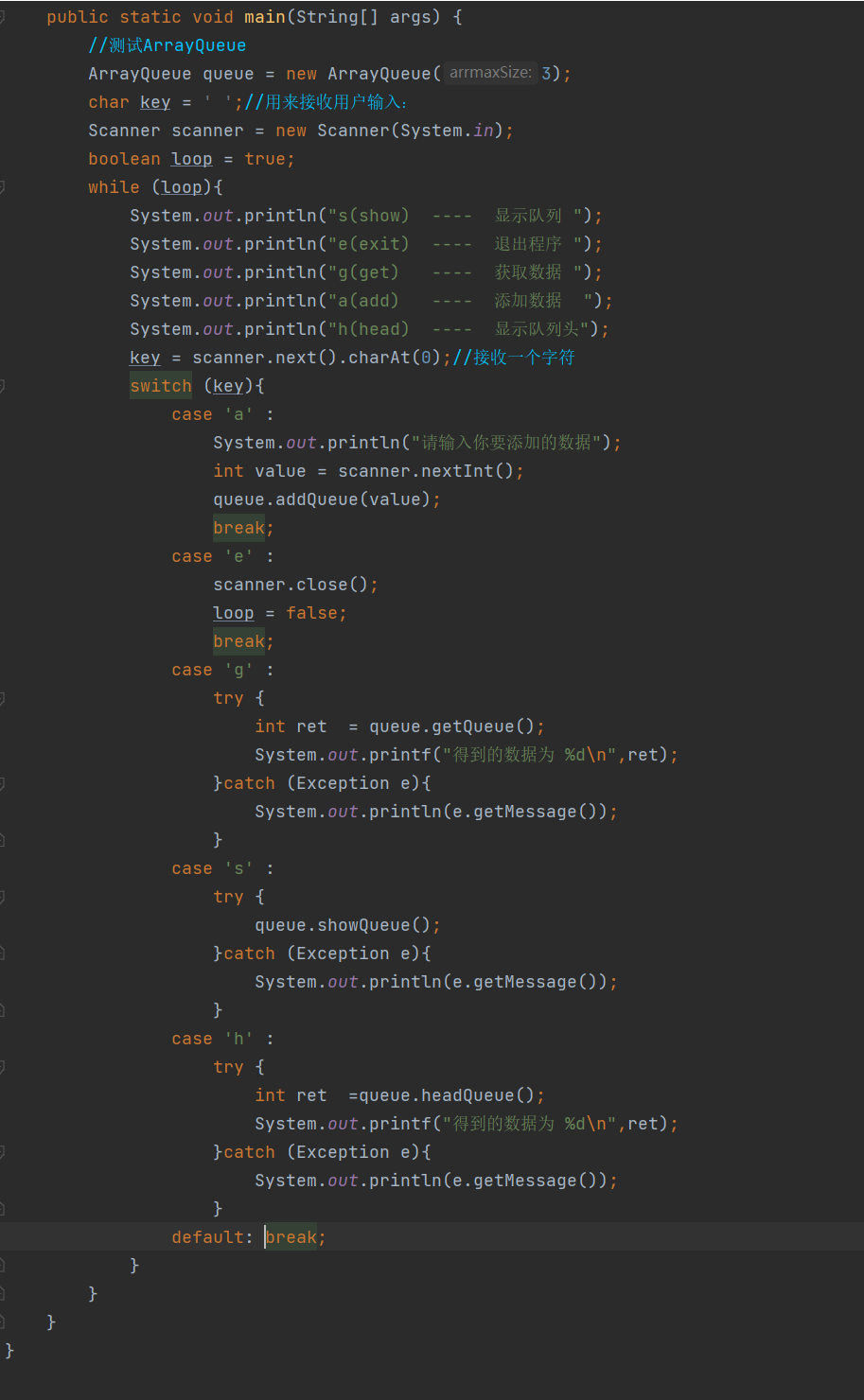
代码实现:
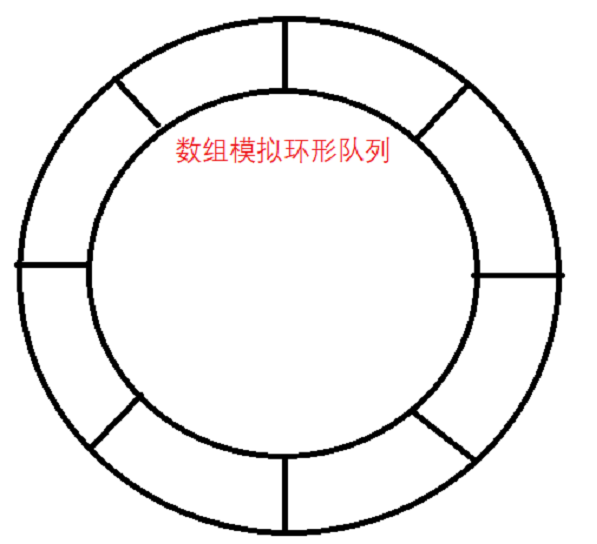
数组模拟环形队列
对于前面数组模拟队列,将数据看做成一个环形(通过取模的方式来实现)
思路分析:
front:指向队列得第一个元素,也就是说arr[front]就是队列的第一个元素,初始值:0
rear :指向队列得最后一个元素的后一个位置,初始值:0
当队列满时,条件是:(rear+1)%maxSize = front 【满】
队列为空时,条件是: rear= front 【空】
public class CircleArrayQueue {
private int maxSize ; //队列的最大容量
private int rear;
private int front;
private int arr[]; //用于存放数据,模拟队列:
//创建队列的构造器:
public CircleArrayQueue(int arrmaxSize) {
maxSize = arrmaxSize;
arr = new int[arrmaxSize];
front = 0 ; //指向队列的头部,
rear = 0 ; //指向对列尾部,指向队列尾的后一个
}
//判断队列是否为空!
public boolean isEmpty(){
return front == rear ;
}
//判断队列是否已满
public boolean isFull(){
return (rear+1)%maxSize == front;
}
//添加数据:-----也就是入队列
public void addQueue(int n ){
//判断是否已满
if (isFull()){
System.out.println("队列已满,不能在添加数据了~~");
return;
}
arr[rear] = n ;
rear = (rear+1)%maxSize; //这里必须考虑取模
}
//获取队列数据--也就是出队列
public int getQueue(){
//判断队列是否为空!
if (isEmpty()){
throw new RuntimeException("队列为空,不能在获取数据~~~");
}
int value = arr[front] ;
front = (front +1)%maxSize;//需要考虑取模!
return value;
}
// 表示当前数据的有效个数!
public int size(){
return (rear+maxSize-front)%maxSize;
}
//显示队列的所有数据:
public void showQueue(){
if (isEmpty()){
throw new RuntimeException("队列为空,没有数据~~~");
}
//思路:从front 开始遍历,遍历多少个元素---(rear+maxSize-front)%maxSize:表示当前数据的有效个数!
for (int i = front; i < front+ size(); i++) {
System.out.printf("arr[%d] = %d\n" ,i%maxSize,arr[i % maxSize]);
}
}
//显示对列的头部:不是取数据:
public int headQueue(){
if (isEmpty()){
throw new RuntimeException("队列为空,没有数据~~~");
}
return arr[front];
}
}
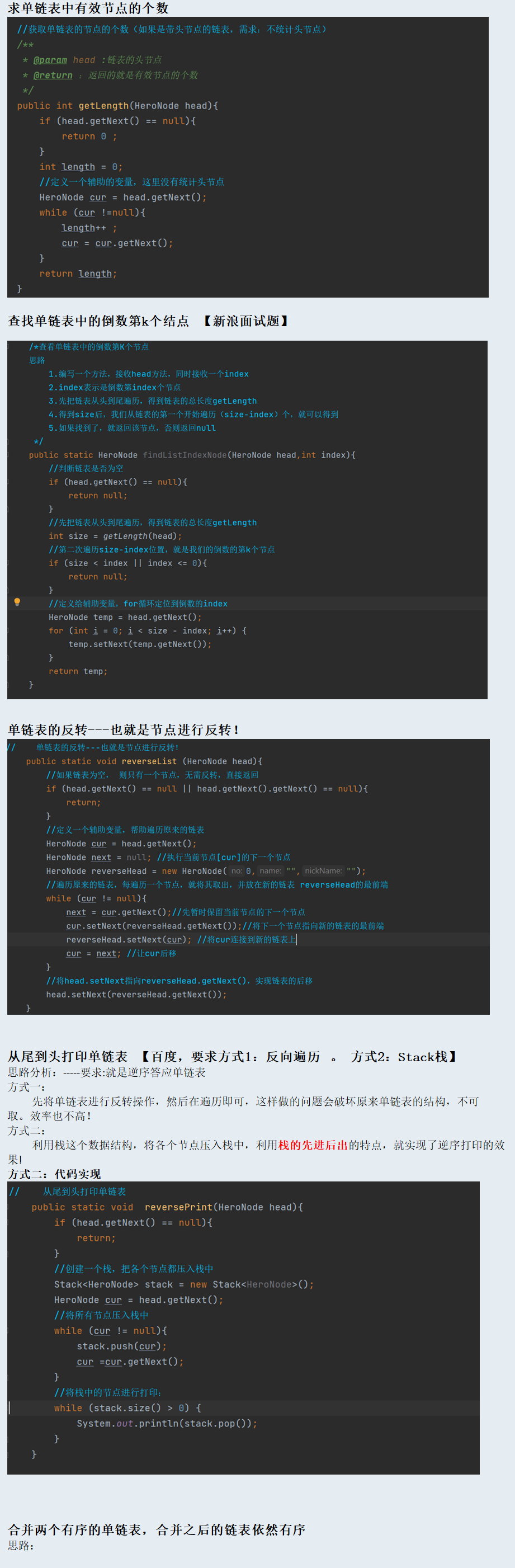
单链表

单链表面试题
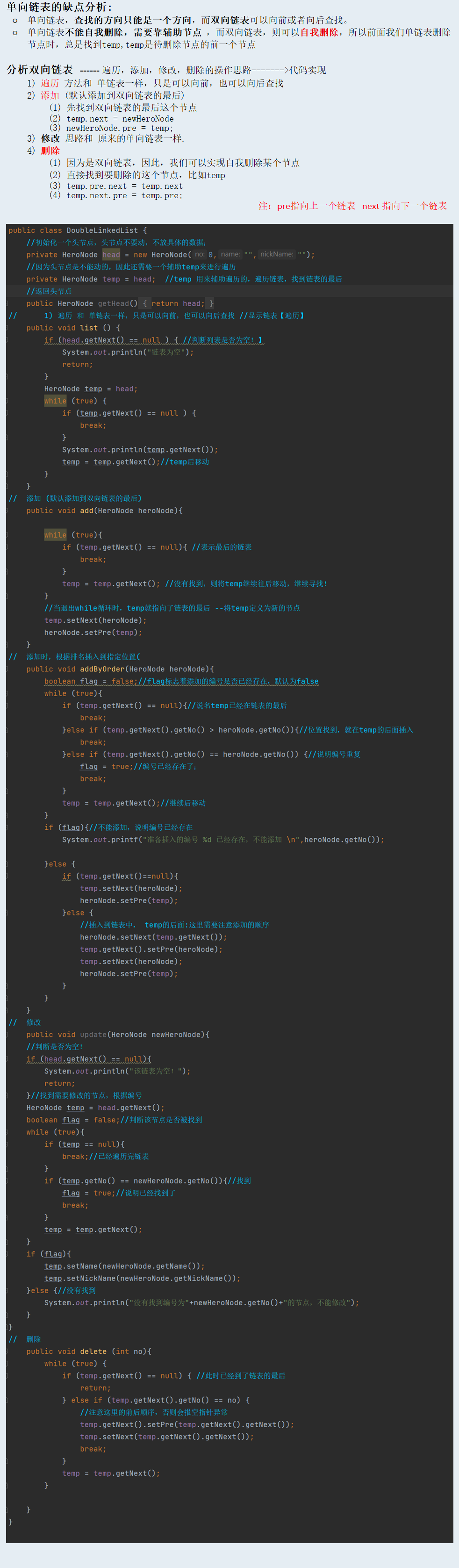
双向链表
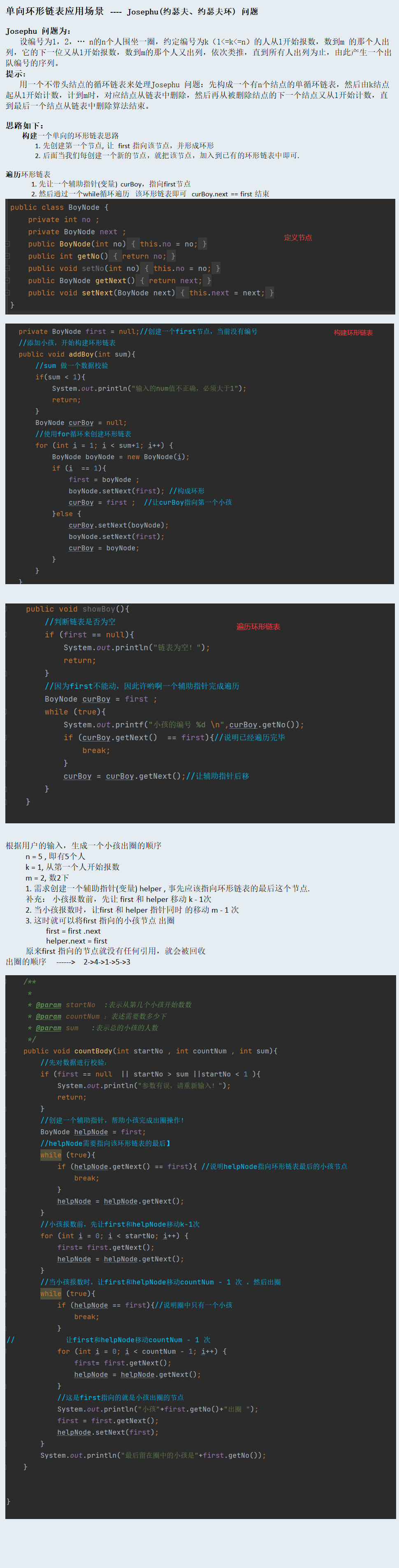
环形链表
栈

前中后缀表达式

递归

排序算法

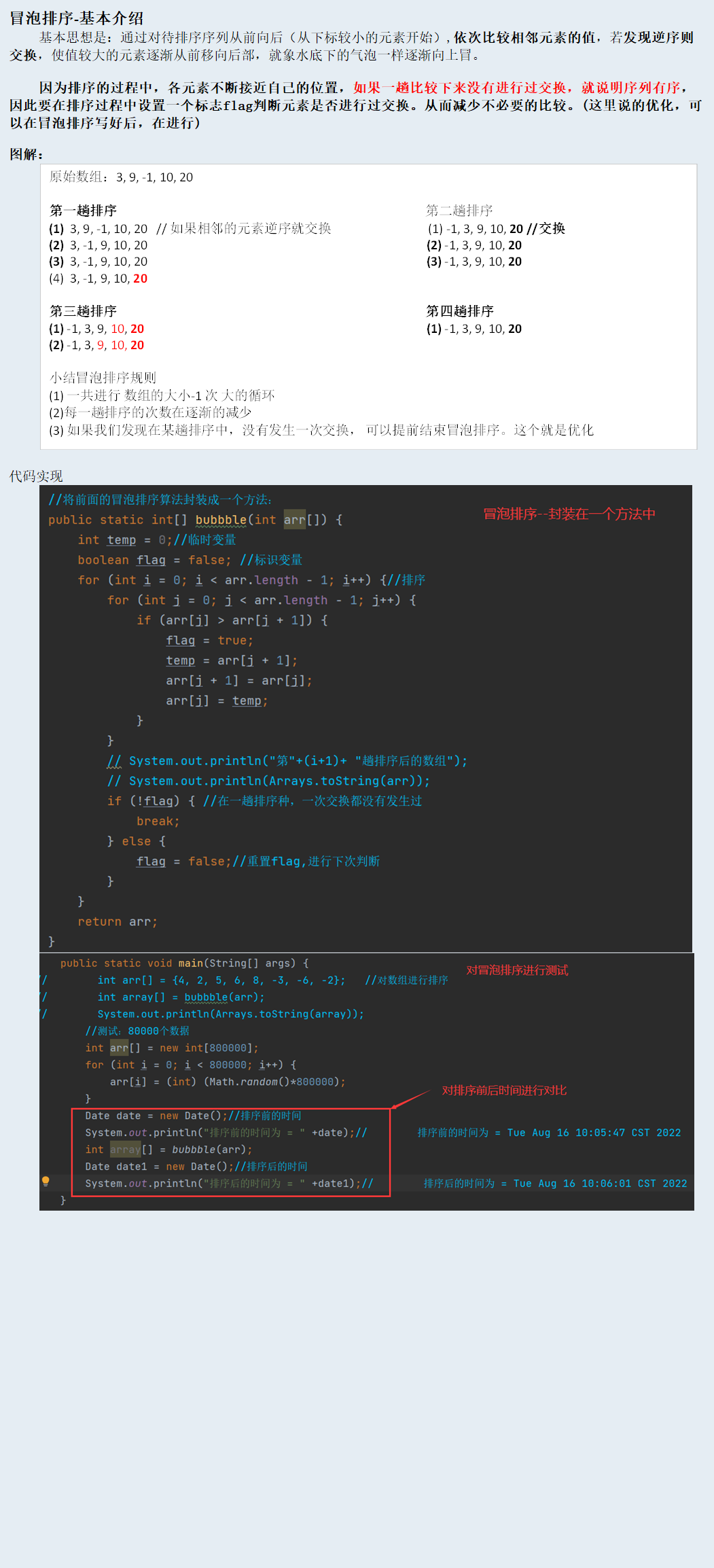
冒泡排序
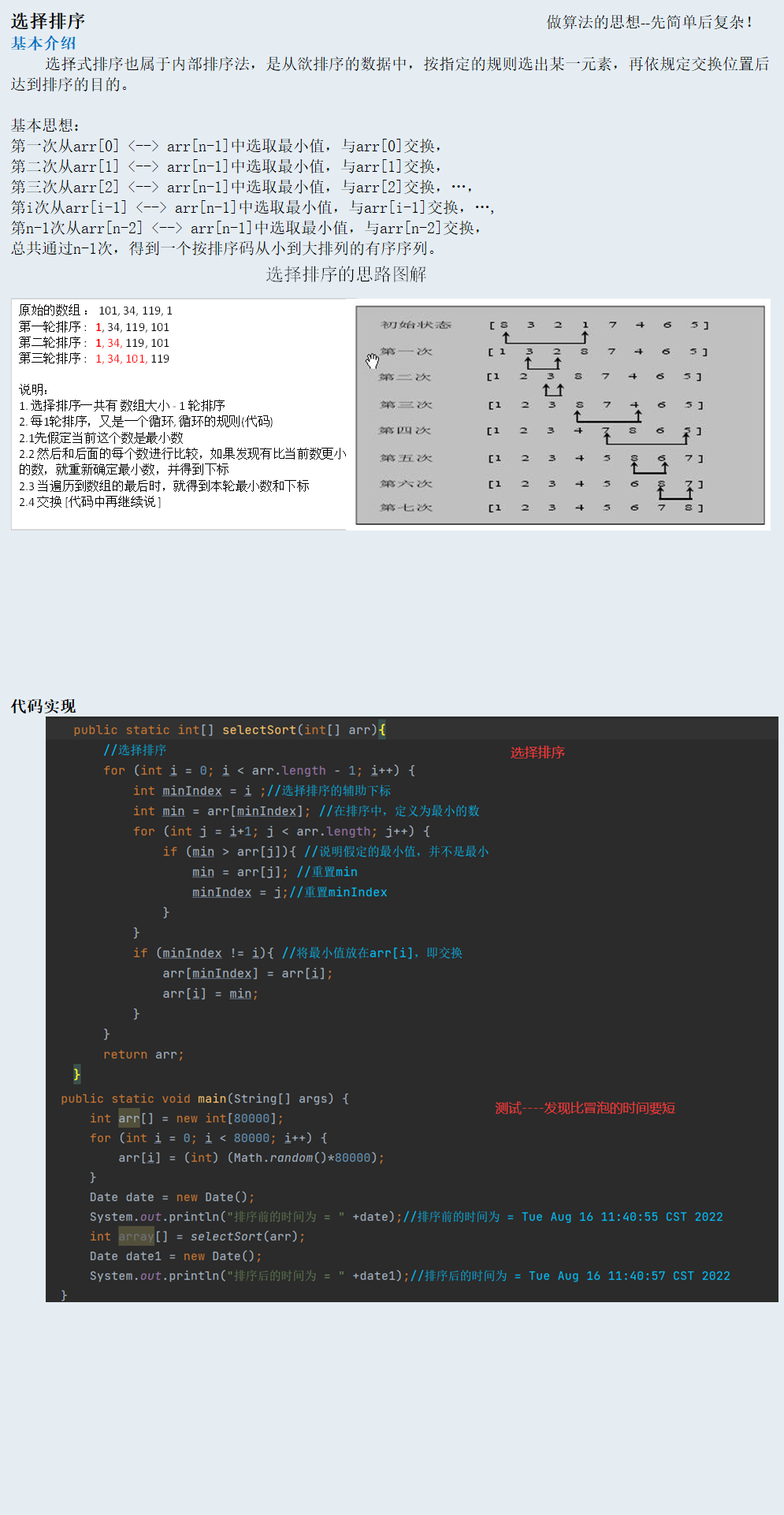
选择排序
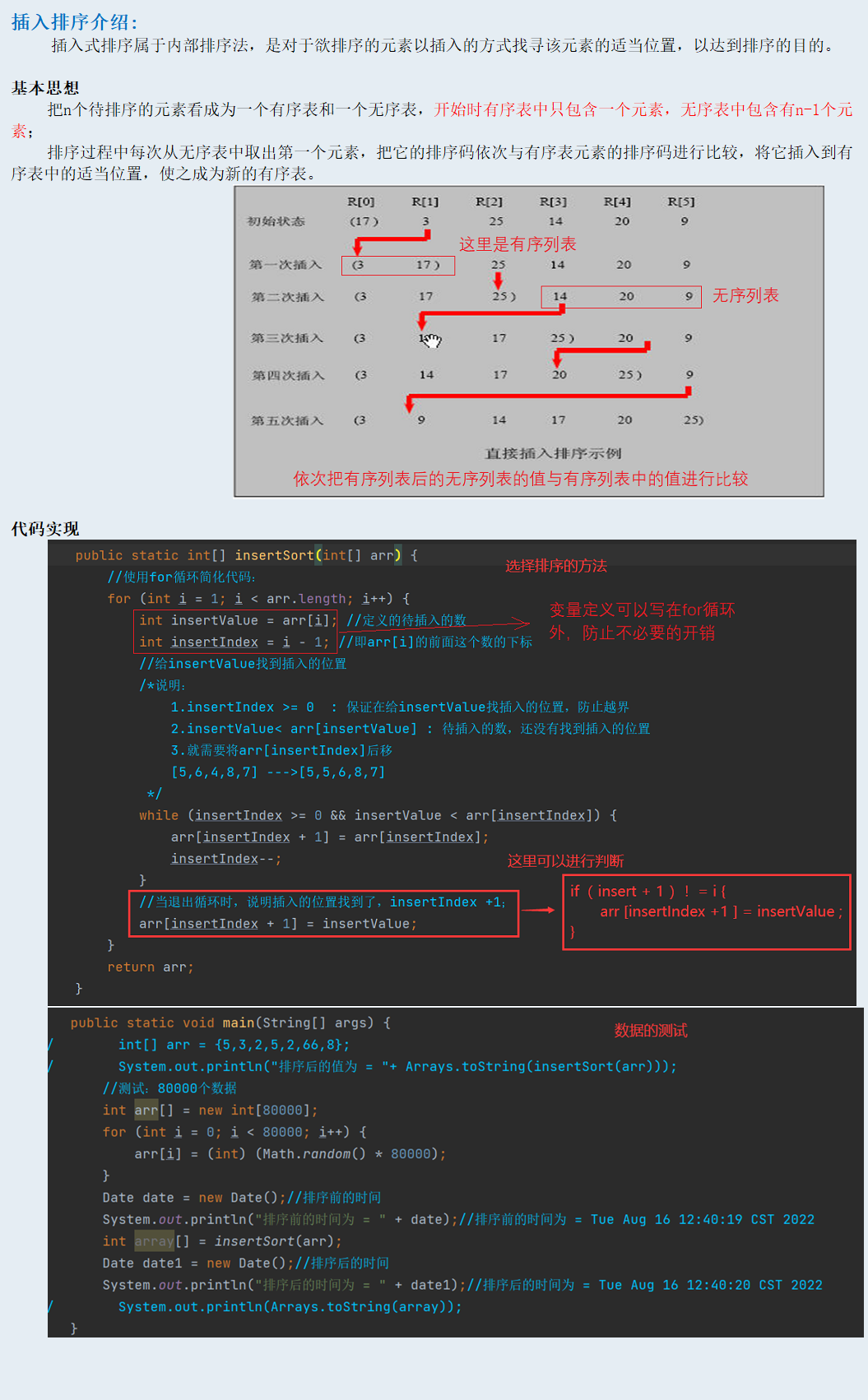
插入排序
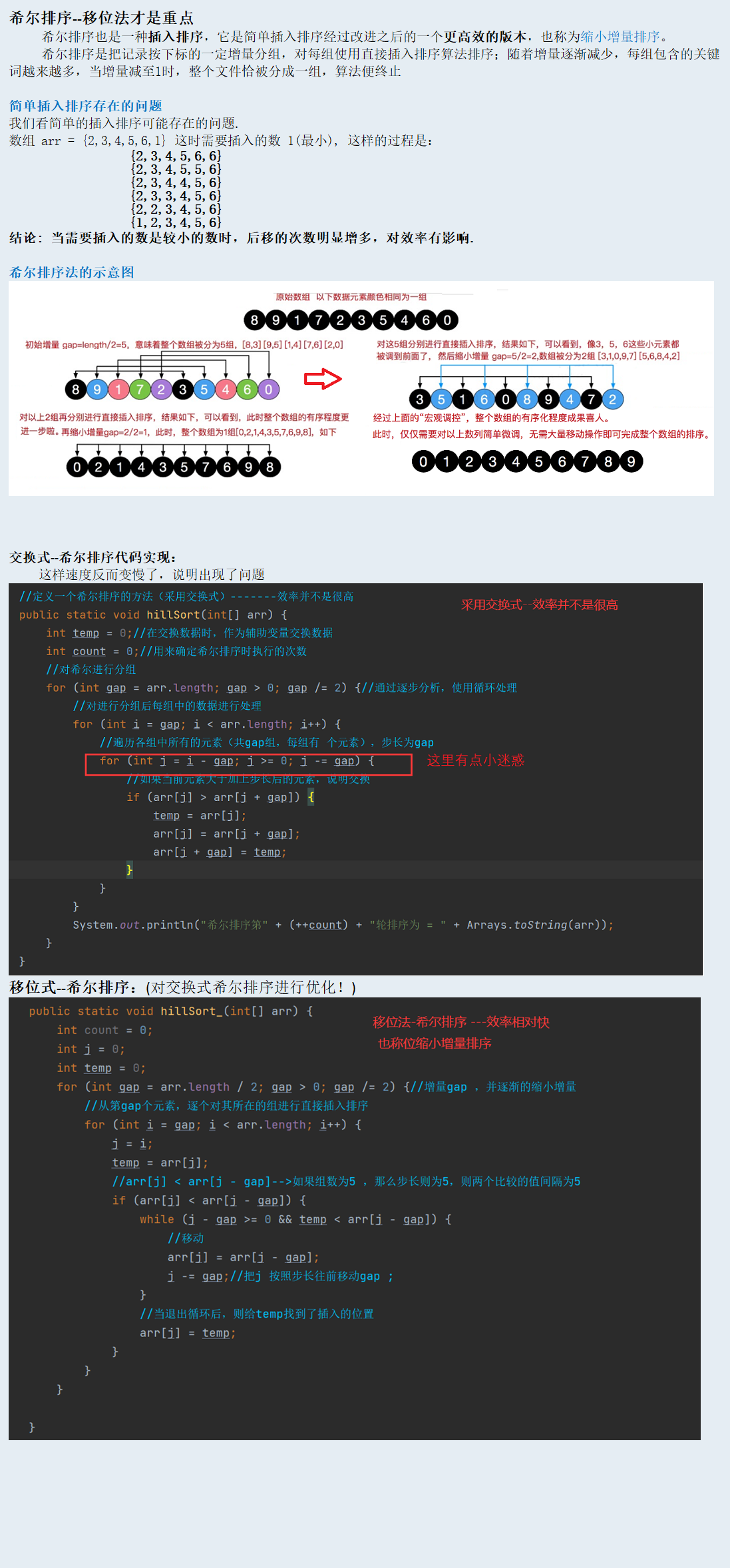
希尔排序
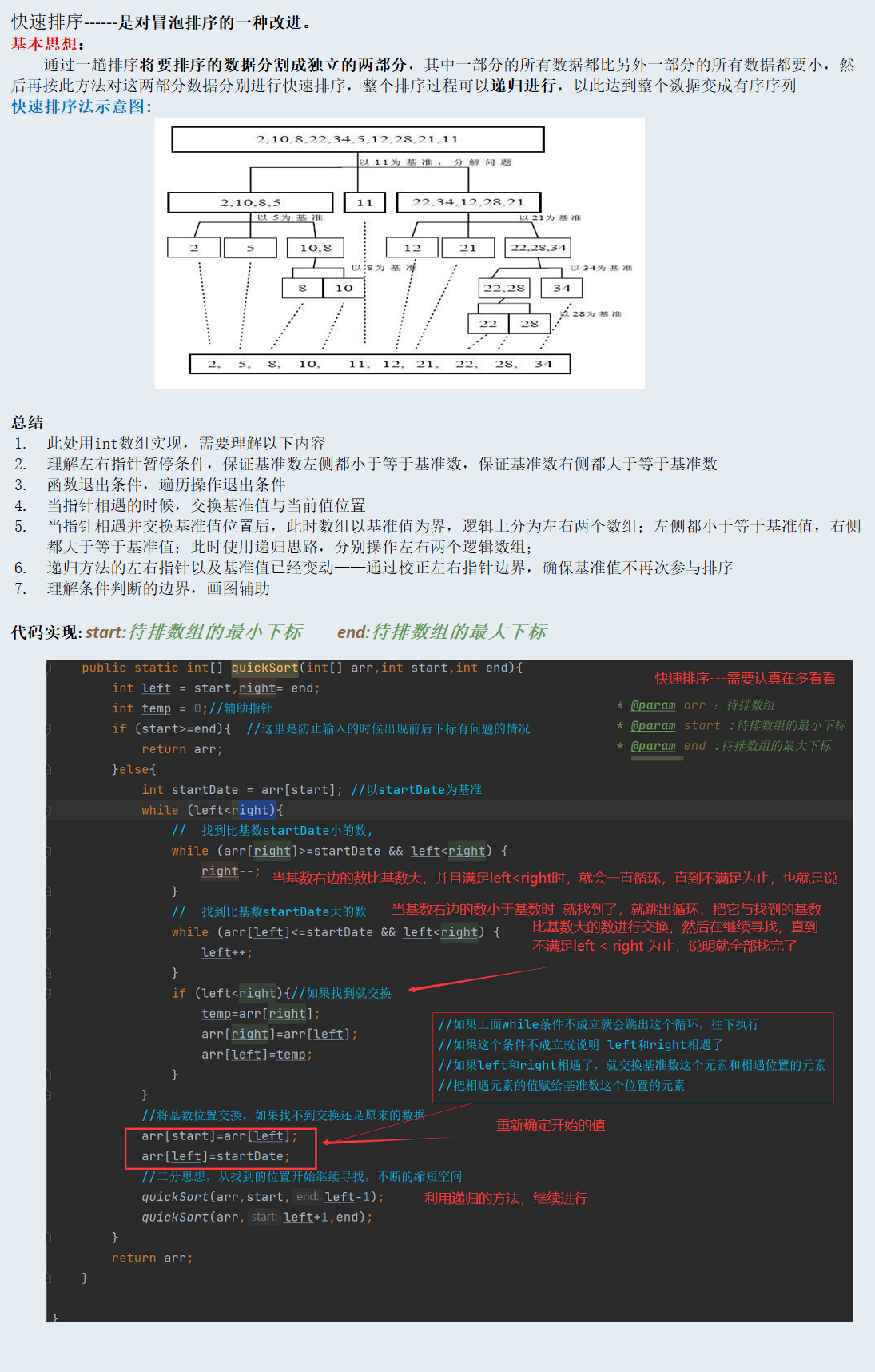
快速排序
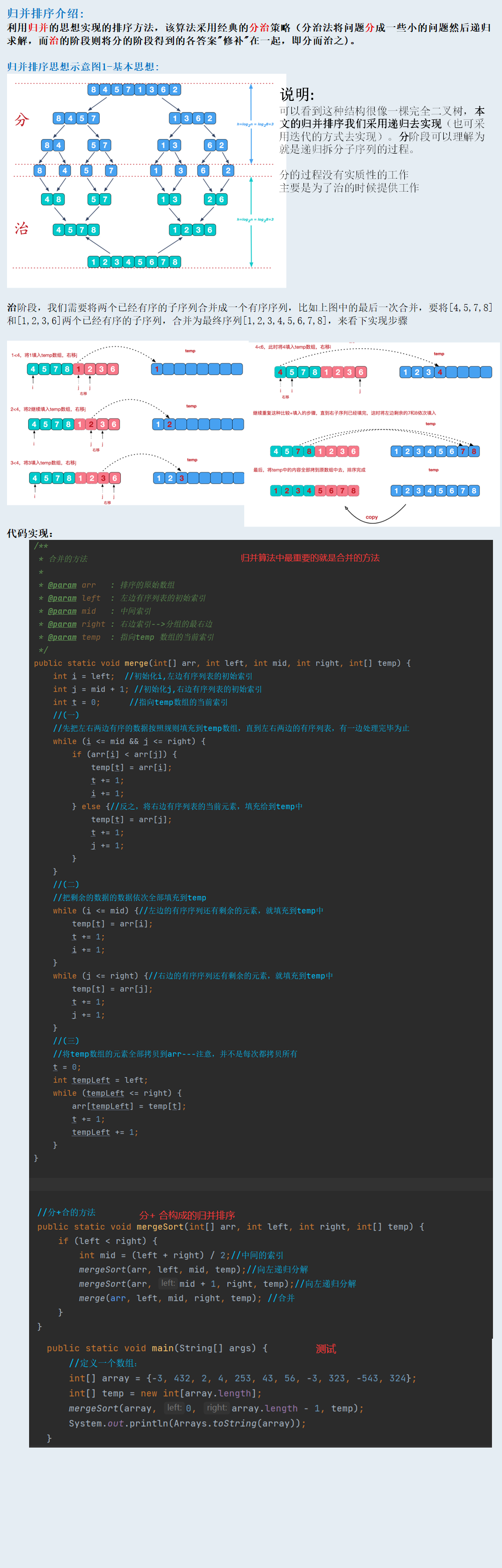
归并排序
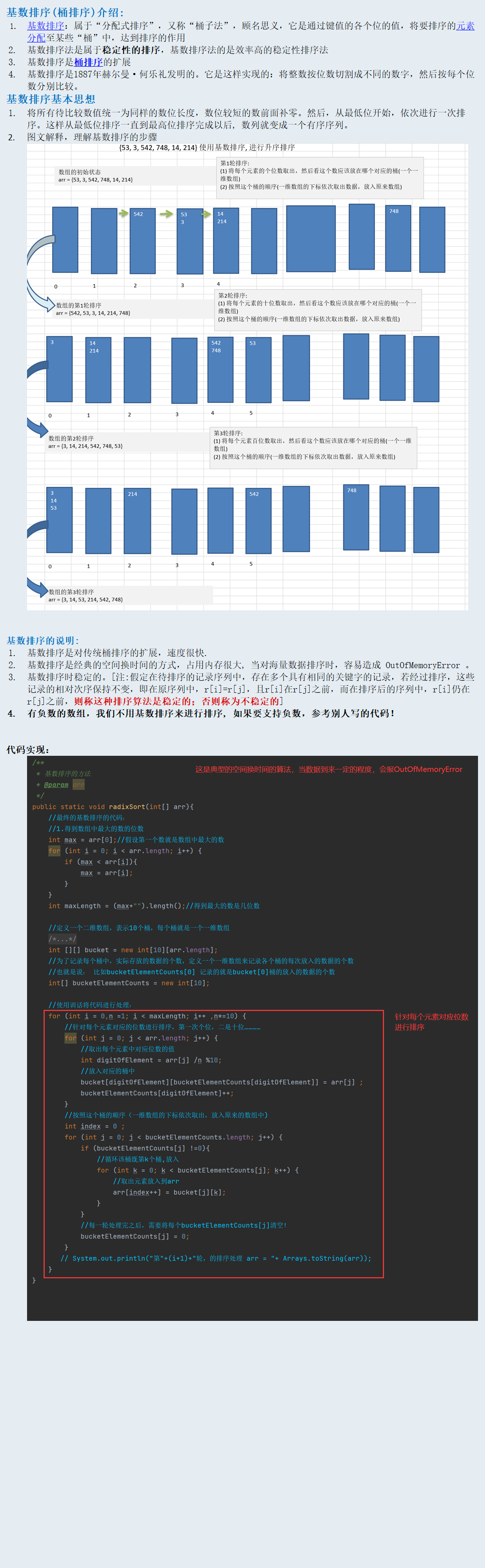
基数排序
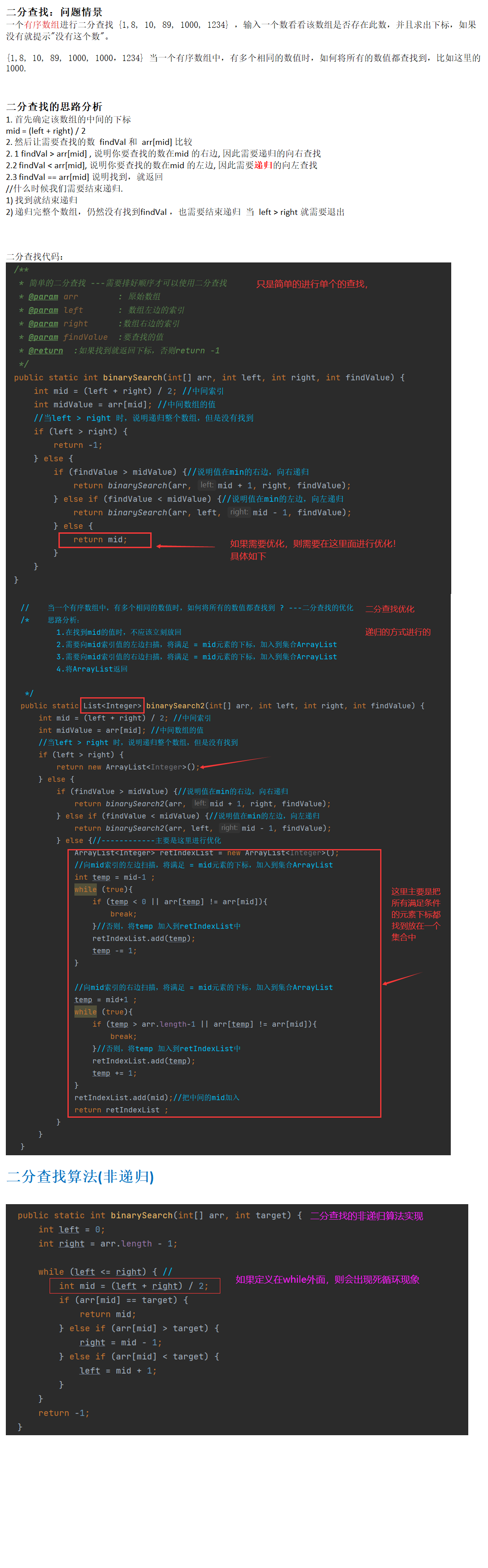
二分查找/折半查找
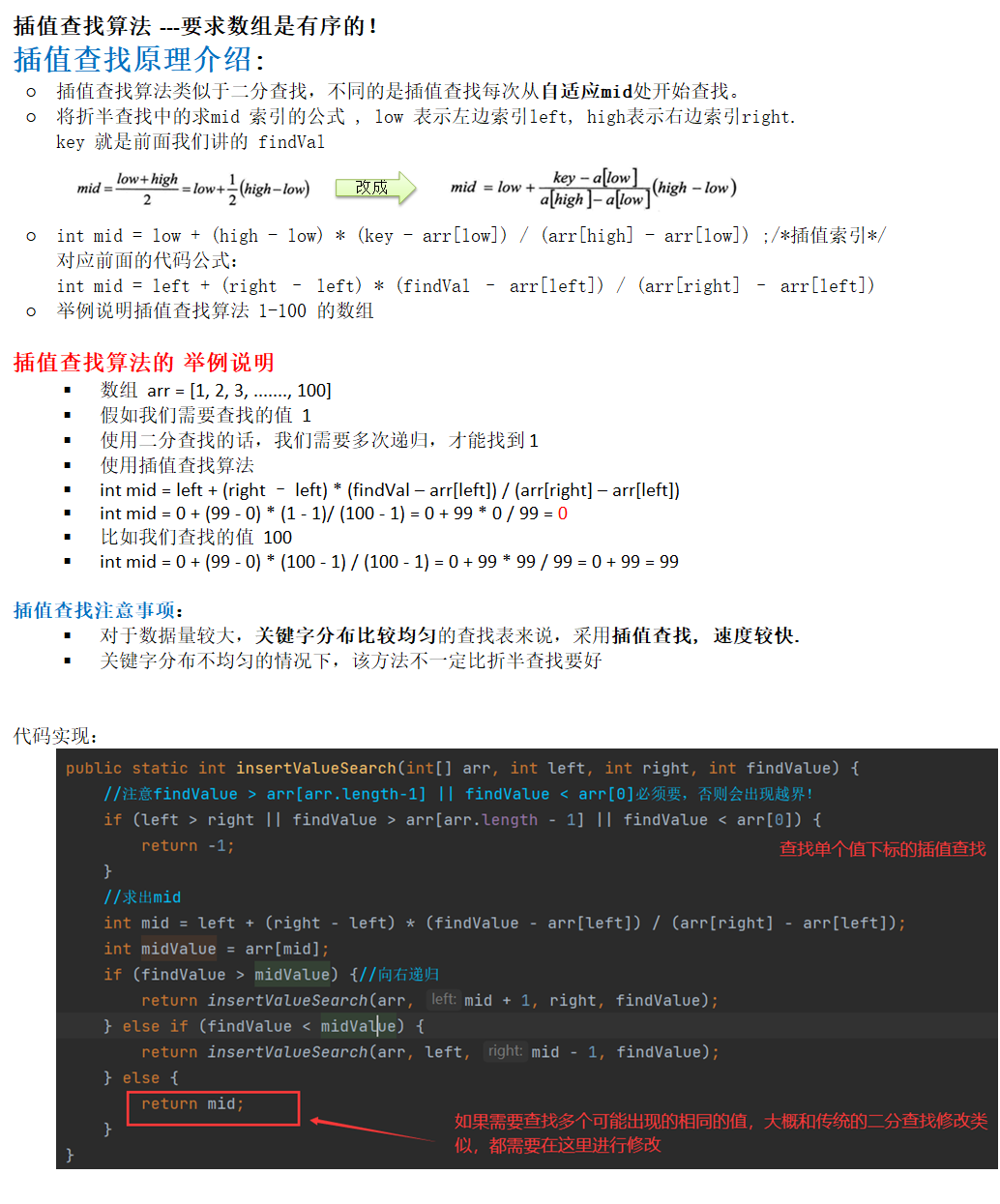
插值查找
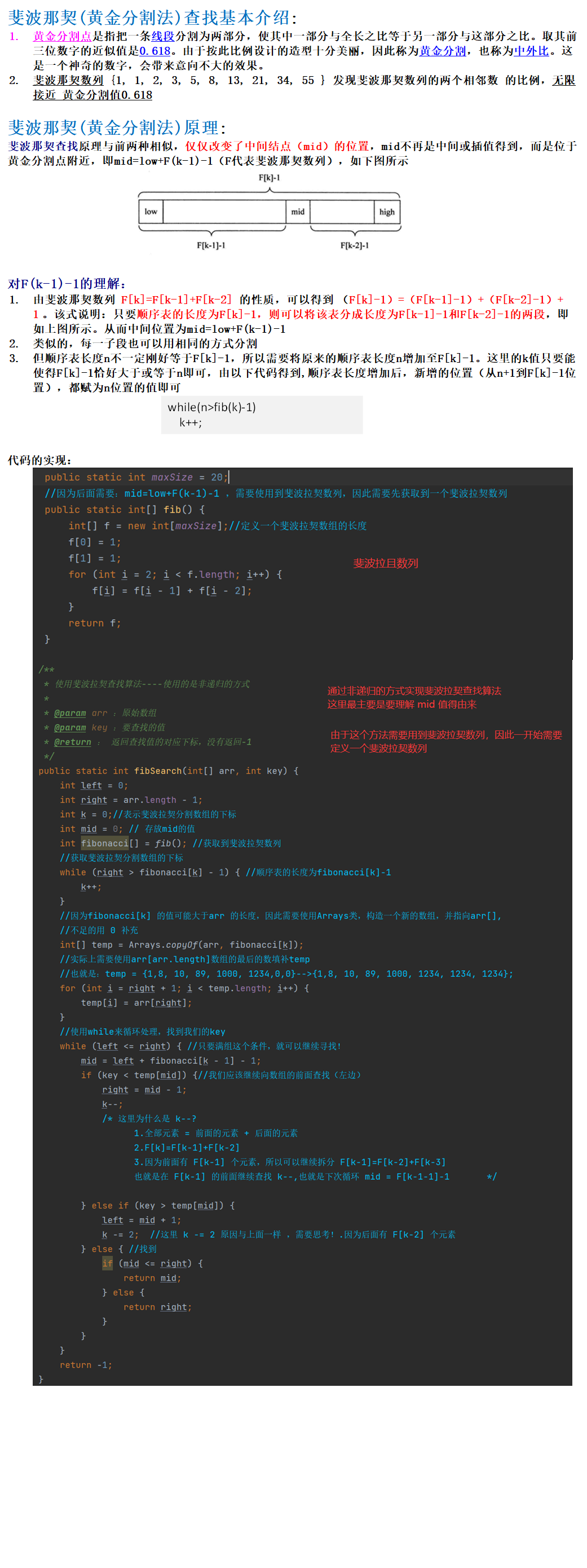
斐波那契查找
哈希表

树结构-二叉树

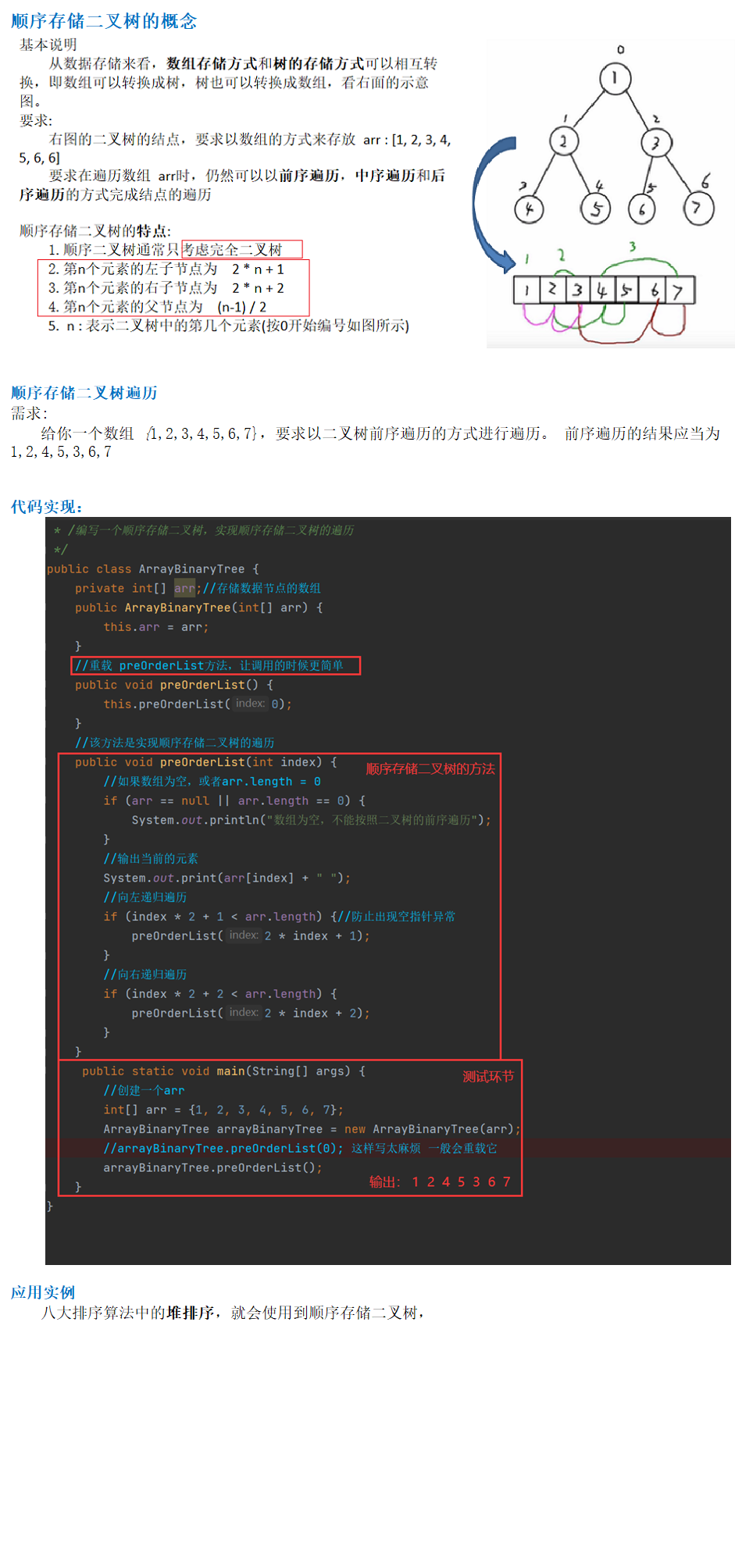
顺序存储二叉树
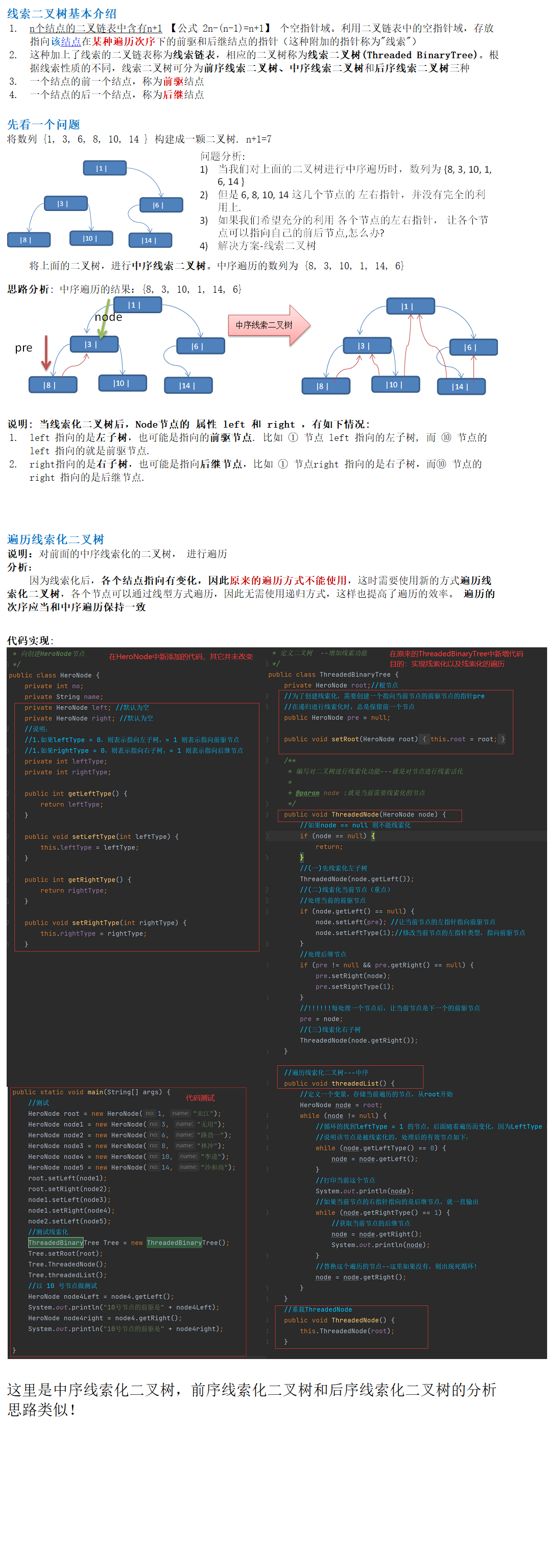
线索化二叉树
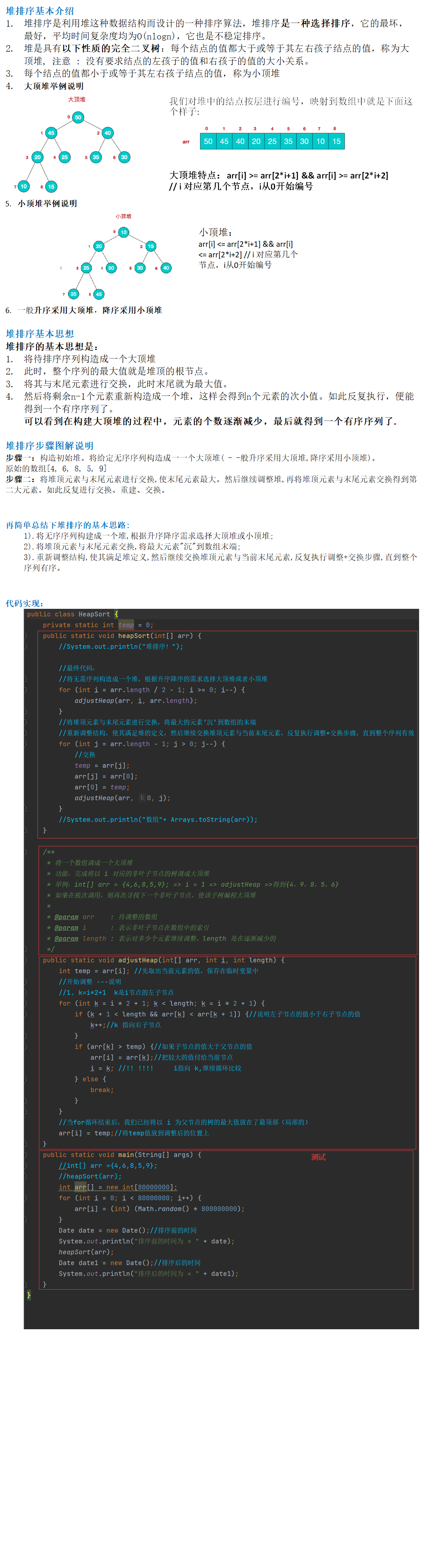
堆排序
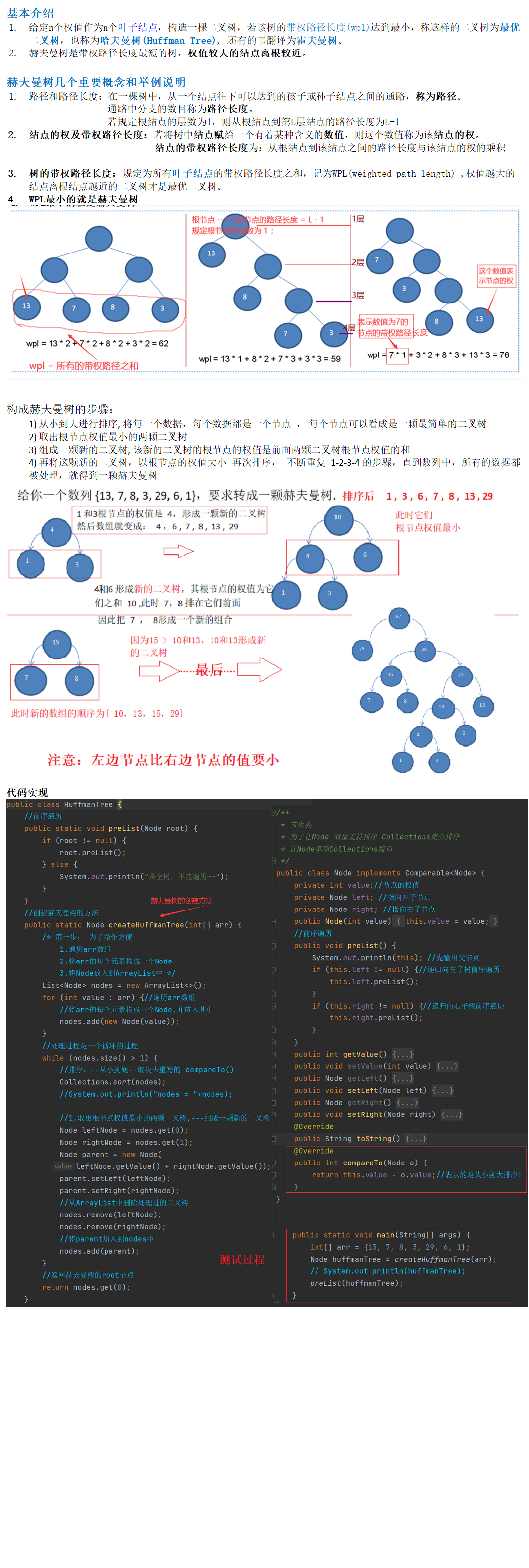
赫夫曼树
赫夫曼编码

二叉排序树-BST

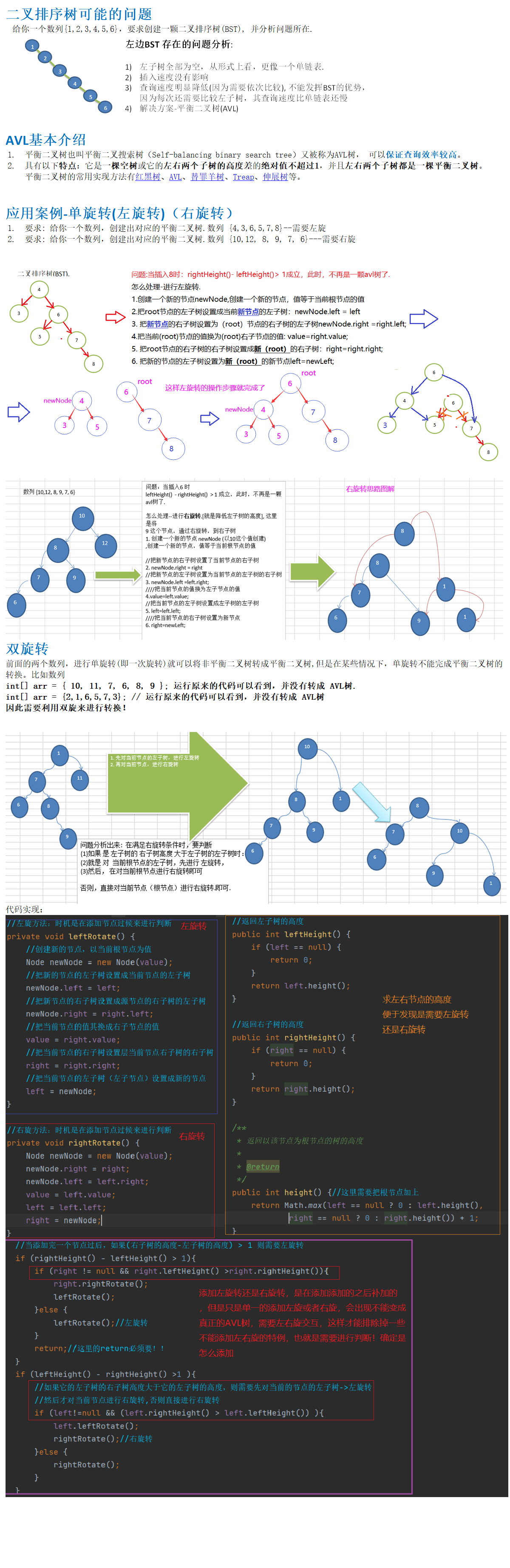
平衡二叉树-AVL
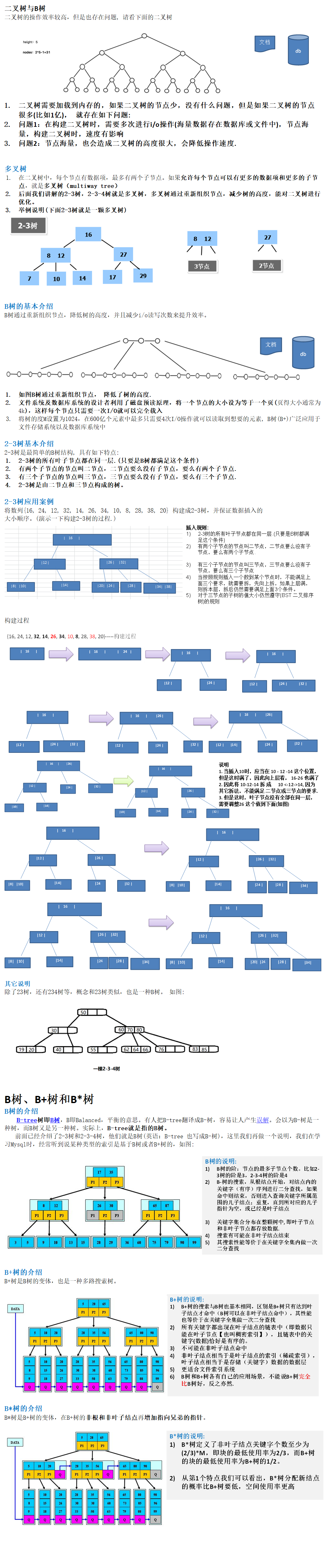
多路查找树-了解
图

常用算法-分治算法

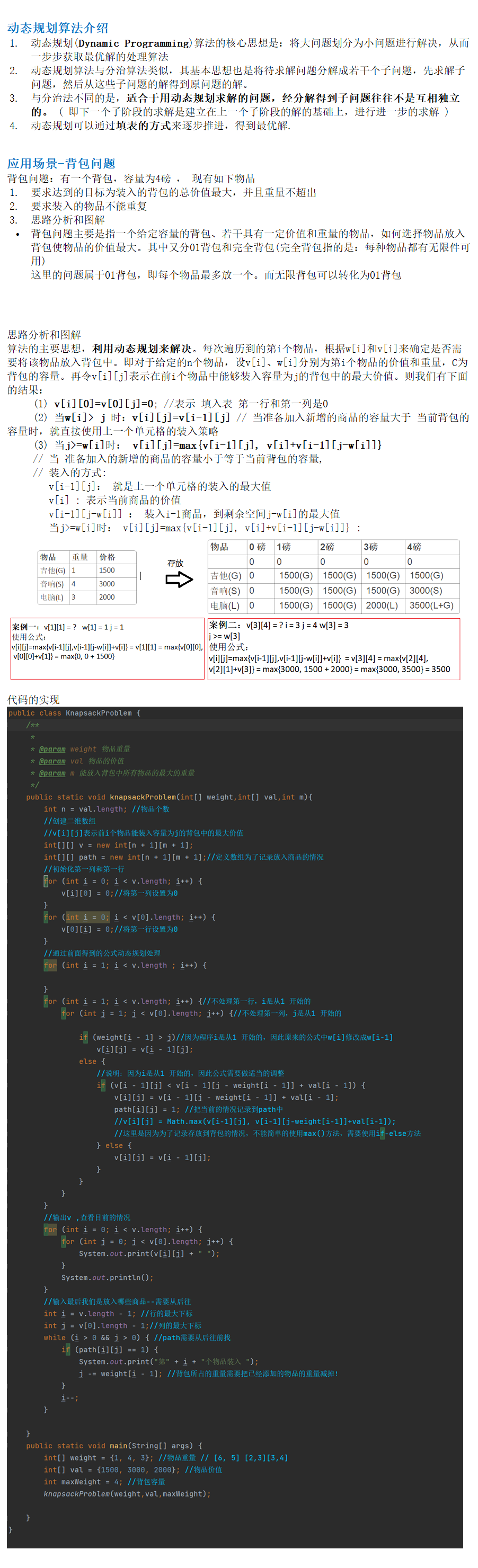
动态规划算法
KMP算法

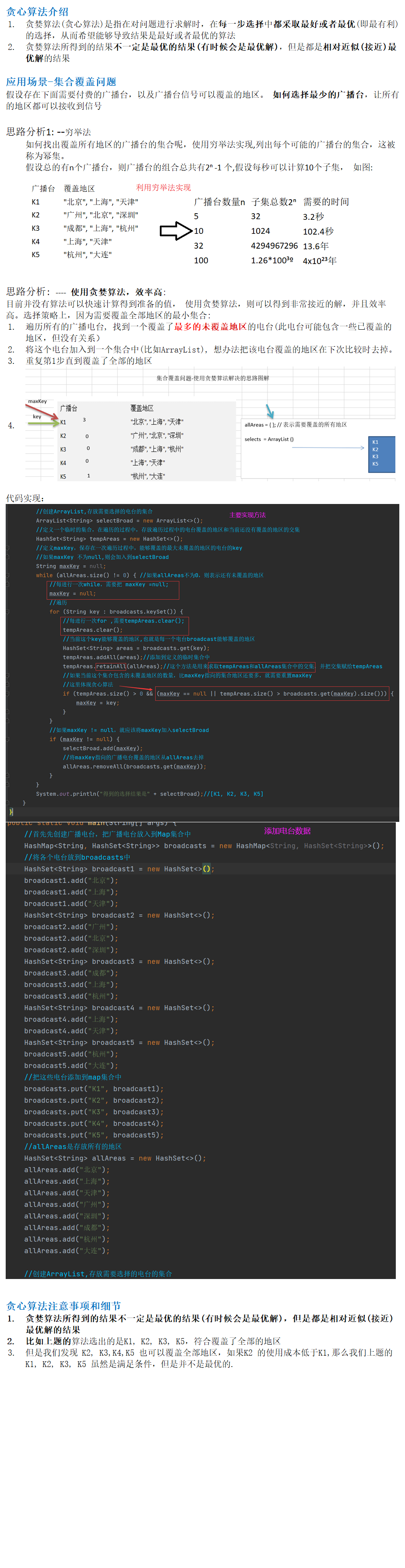
贪心算法
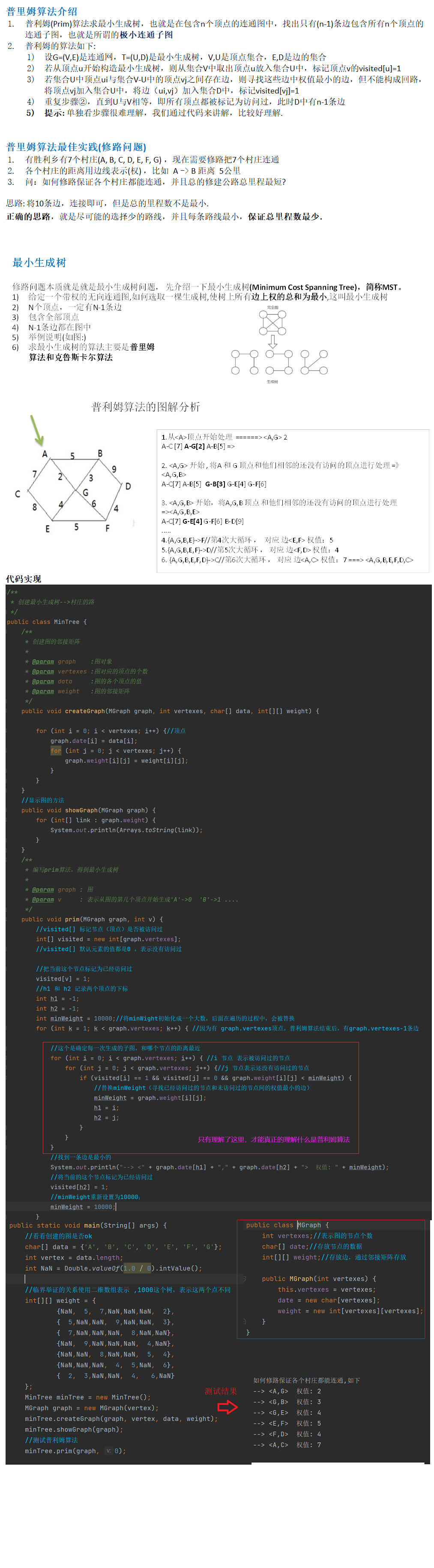
普利姆算法
克鲁斯卡尔算法

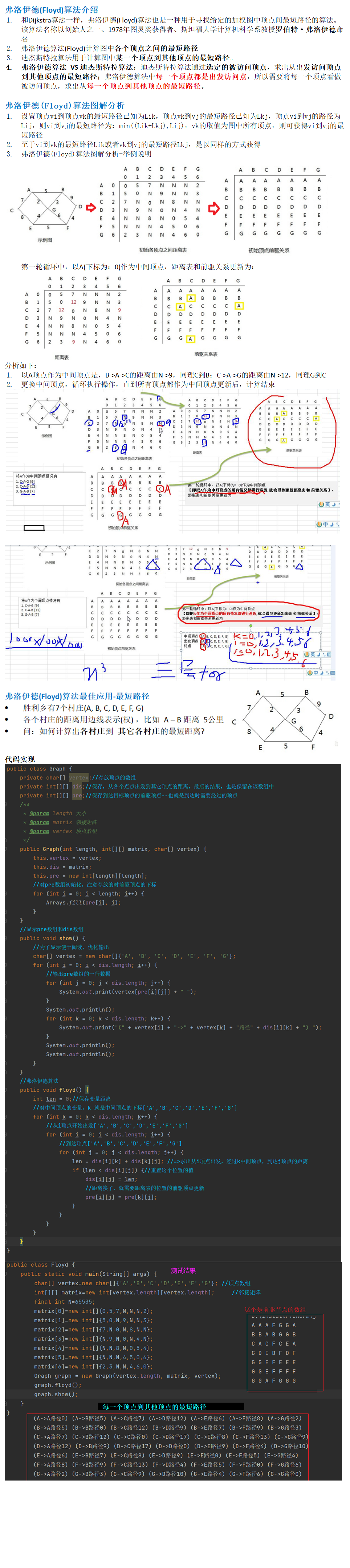
迪杰斯特拉算法

弗洛伊德算法
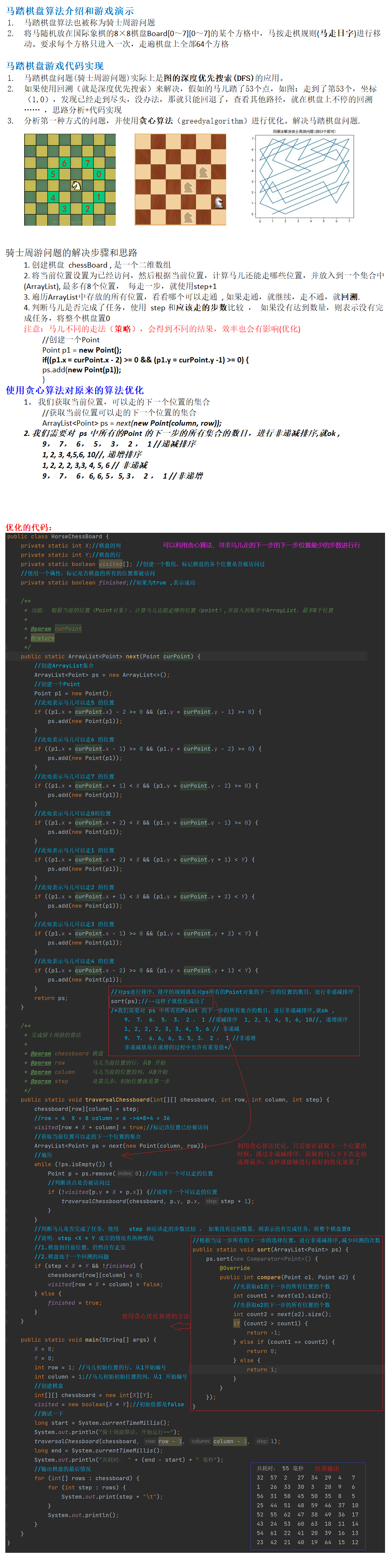
马踏棋盘算法



 浙公网安备 33010602011771号
浙公网安备 33010602011771号