leetcode之62不同路径Golang

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

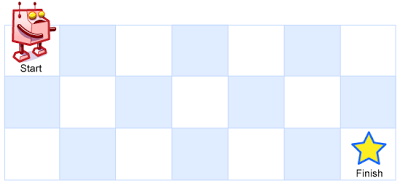
例如，上图是一个7 x 3 的网格。有多少可能的路径？

示例 1:

输入: m = 3, n = 2
输出: 3
解释:
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右

示例 2:

输入: m = 7, n = 3
输出: 28

提示：

• 1 <= m, n <= 100
• 题目数据保证答案小于等于 2 * 10 ^ 9

算法

这道题和55题的跳跃游戏有很大的相似之处，我们依然采用动态规划的方法解决本题，我们定义一个和地图一样大的二维数组，二位数组中每个位置保存的是从起点到该位置的不同路径的数量

那么从开始位置开始，到开始位置自然只有1种路径，然后第二个位置，到第二个位置同样只有一种路径，因为第二个位置在起始位置的右边，而它们的上面没有位置，所以只可能从左边到第二个位置这一种走法，然而到它的左边的位置也就1种路径

总的来说，本算法是求开始位置到当前位置的不同路径的数量，那么通常情况下，到当前位置有两种走法，就是从上面走下来和从左边走过来，所以到当前位置的不同的路径也就是上面的那个位置的路径数量加上左边那个位置的路径数量

代码

func uniquePaths(m int, n int) int {
	paths := make([][]int, m)
	for i := 0; i < len(paths); i++ {
		paths[i] = make([]int, n)
	}
	for row := 0; row < m; row++ {
		for column := 0; column < n; column++ {
			switch {
			case row-1 < 0 && column-1 < 0:
				paths[row][column] = 1
				// continue
			case row-1 < 0 && column-1 >= 0:
				paths[row][column] = paths[row][column-1]
			case row-1 >= 0 && column-1 < 0:
				paths[row][column] = paths[row-1][column]
			default:
				paths[row][column] = paths[row][column-1] + paths[row-1][column]
			}
		}
	}
	return paths[m-1][n-1]
}