leetcode之最长回文子串Golang(马拉车算法Manacher‘s Algorithm)

最开始尝试的是暴力破解的方法求最长的回文子串，可是总是超时，因为暴力破解方法的时间复杂度是O(N³)然后去查了一下求回文子串的方法，发现了这个马拉车算法（Manacher's Algorithm）

马拉车算法求最长的回文子串的时间复杂度是O(N)

奇数化字符串

回文字符串有奇偶两种形式：a aba bb abba

所以为了避免我们在算法中对奇偶两种形式分开讨论，我们就将这两种形式都转化为奇数形式（也就是回文串的总的字符数是奇数个），方法就是在每个字符之间的空隙之间加入特殊字符，例如：　　

a　　==>　　#a#

aba　　==>　　#a#b#a#

bb　　==>　　#b#b#

因为字符数加上他们之间的空隙数的总数总是为奇数（空隙数比字符数多一个，两个相邻的数字加起来和为奇数），所以通过这种方式，我们可以将字符串处理为总数为奇数

 回文串的半径

通过上面我们的处理以后，我们在定义回文串的半径，也就是回文串长度的一半

#a#　　==>　　半径为2

#a#b#a#　　==>　　半径为4

半径就是奇数回文串的长度加1，然后除以2得到的结果

通过我们处理以后的回文串的半径，我们能够很容易的得到原来回文串的长度，原来回文串的长度就是处理后的回文串的半径减1，例如：

#a#　　==>　　半径为2　　==>　　原来回文串的长度为2-1=1

#a#b#a#　　==>　　半径为4　　==>　　原来回文串的长度为4-1=3

#b#b#　　==>　　半径为3　　==>　　原来回文串的长度为3-1=2

有了回文串的长度，我们只需要知道在最开始的字符串中那个回文子字符串的起始的位置，我们就能够轻松求得回文子串， 如图所示，

第一行表示字符串中每个元素的下标，第二行是处理后的字符串，第三行表示以当前字符为中心的回文串的半径（例如以下标为1的b为中心的回文串是#b#，那么他的半径就是2）

原始的字符串babb，对于原来是偶数的回文子串bb，如图所示，下标为6的#就是这个回文子串的中心，用下标6减去对应的半径3，结果为3，刚好是回文子串bb在原始字符串babb中的位置

但是如果是原来是奇数的回文串，例如bab，那么中心字符在图中对应的就是下标为3的值，它的半径为4，如果相减就得到-1，显然这个-1不会是任何子串在原始字符串中起始位置。

为了统一这两种情况，我们再次对字符串进行如下处理：

　　在处理后的字符串的开始和结尾加两个不同的特殊字符，分别为"$"和"&"，得到结果如下图：

 

 对于新的结果，如图所示，当我们需要求回文串bb的起始位置，那么就是下标为7的#作为中心字符的那个回文串，bb在原始字符串起始位置为(7-3)/2=2

如果求bab的起始位置，就是(4-4)/2=0

如果原始字符串的下标从0开始计数，那么这样得到的结果就刚好是回文子串在原始字符串中的起始位置。

　　综上所述：回文串的长度是中心字符所在位置的半径减1，在原始字符串中的起始位置就是中心字符的位置减去半径的差然后除以2

上面图中的第三行就是马拉车算法的关键结果，下面我们讲怎样求第三行这个数组

求半径数组

整个算法的关键就是这个半径数组P[]

首先是两个临时变量mx和id

　　id是当前求得的所有回文字符串中，右边界最远（就是说这个回文串的最后一个字符的下标最大）的那个回文串的中心位置，mx就是这个字符串的最右边的边界（应该是边界加1）

 

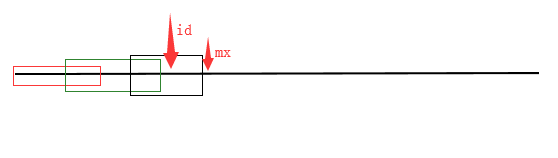
 　　如上图所示，假设上面三个方框是当前阶段求得的三个回文串，那么黑色方框代表的回文串的右边界就是最远的，所以id是黑色方框的中心位置，mx是黑色方框的右边界。

然后看下一个图，就是如何求半径数组的关键部分。

 

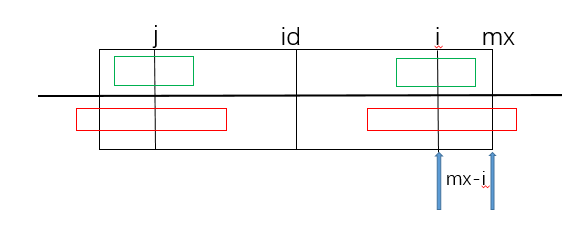
 如上图所示，右边界最远的回文串是黑色方框所代表的，他的中心是id，右边界是mx，此时我们要求下标为i的字符为中心的回文串的半径，这个图代表的情况是i<=mx的情况，j是i关于id对称的点，由于j在i之前，所以我们当我们在求i点的值的时候，j点的值已经被我们之前计算出来了。然后分两种情况，分别如上图的绿色框和红色框：

　　此时的条件是mx>=i

　　首先是绿色框，如图所示，绿色框是被完全包含在黑色大框中的，左边的绿色框表示以j点的字符为中心的回文串，由于整个黑色大框也是一个回文串，并且i和j还是关于黑色大框的中心id对称，所以必定右边的绿色框也是一个回文串，所以P[i]=[j]。

　　　　此时的判断条件是P[j]<=mx-i;j=id-(i-id)=2*id-i

　　然后是红色框，如图所示，红色框的部分已经超出了黑色大框，但是根据对称性，在上图中，mx-i的那一部分还是黑色框的一部分，由j点和i点对称，可以知道mx-i的那一部分和它关于i点对称的那部分是一样的，也就是i的两边mx-i这个长度的字符串是回文串，所以此时P[i]至少等于mx-i。为了计算此时的具体的P[i]，我们只需要看超出mx点的字符与关于i点对称的字符是否相等，如果相等，那么P[i]就增加，否则就返回这个P[i].

　　　　此时的判断条件是P[j]>mx-i

另一种情况就是i>mx，此时上图所说的条件就不成立了，那么处理的方法直接就是P[i]=1

 

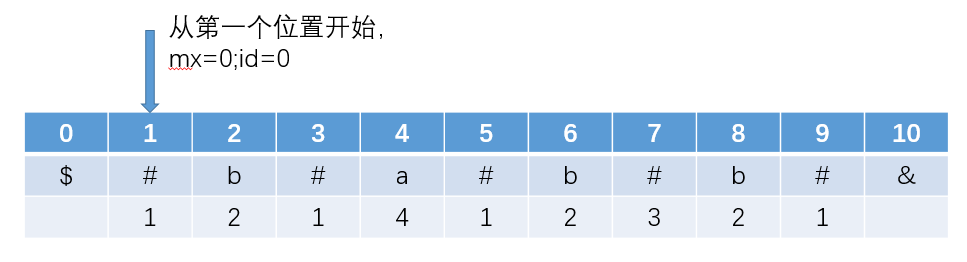
 从第一个位置开始遍历一遍，就可以求得每一个位置的P[i]，值得注意的是，每次求的一个P[i]以后（求得一个P[i]就相当于求得一个回文串），需要判断这个回文串的右边界是否超出了mx，如果超出了，就需要更新mx和id的值，将他们换成当前右边界最远字符串的id和mx。

　　由边界数组就能够求得每一个回文子串了，自然就能够求得最长的回文子串了。

上代码

下面是Golang的实现方法：

func longestPalindrome(s string) string {
	// 对字符串进行处理，在每个字符串中间加上一个#，并且在最前面加$，最后面加&
	tmpString := "$#"
	for i := 0; i < len(s); i++ {
		tmpString += string(s[i])
		tmpString += "#"
	}
	tmpString += "&"
	// 例如原字符串是abc，那么处理后就是$#a#b#c#&
	// 使用数组来保存每个元素作为回文串中心的半径
	p := make([]int, len(tmpString))
	// id是所有回文串中能延伸到最右端的回文串的中心点，mx是该回文串的最右端
	mx, id := 0, 0
	maxLength, maxIndex := 0, 0
	for i := 1; i < len(tmpString); i++ {
		if mx < i {
			p[i] = 1
		} else {
			if (mx - i) < p[(2*id-i)] {
				p[i] = mx - i
			} else {
				p[i] = p[2*id-i]
			}
			// 然后继续判断后面的字符是不是相同的
			for j := p[i]; i+j < len(tmpString) && j < i; j++ { //防止数组越界
				if tmpString[i+j] == tmpString[i-j] {
					p[i]++
				} else {
					break
				}
			}
		}
		// 更新id和mx的值
		if mx < (i + p[i]) {
			id = i
			mx = i + p[i] //这里mx实际上的值实际上是当前回文串的右边界加1
		}
		if p[i] > (maxLength) {
			maxLength = p[i]
			maxIndex = (i - p[i]) / 2
		}
	}
	// 返回字符串
	resultString := ""
	for k := 0; k < maxLength-1; k++ {
		resultString += string(s[maxIndex+k])
	}
	return resultString
}