2024沈阳站K题

首先先来考虑最简单的一种情况，不反弹，此时答案路线应为多边形某两顶点连线，枚举求解即可。
对于反弹一次的情况，不妨先来看三角形反弹一次的情况。

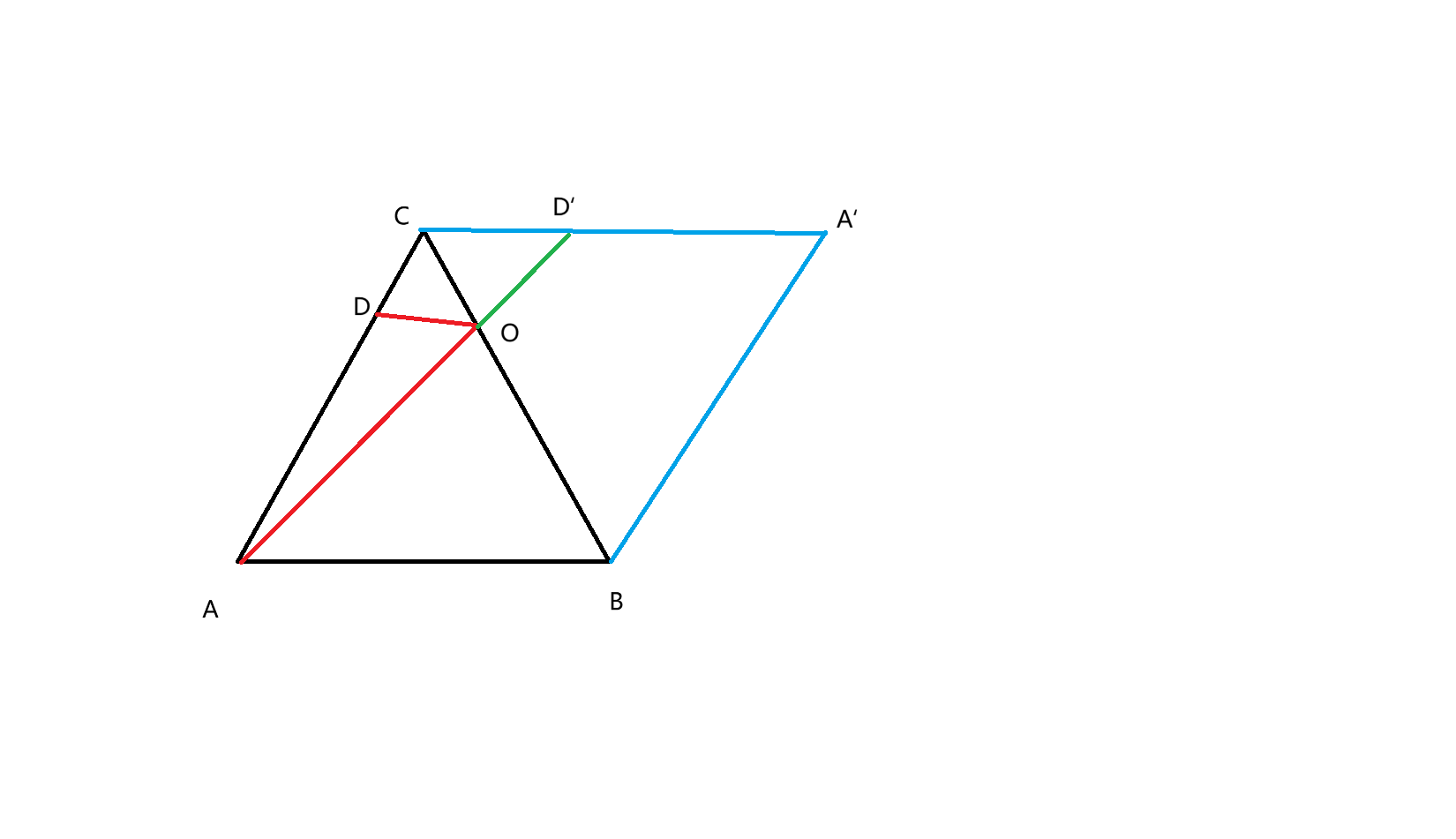
在这个图中光路为A->O->D
我们将三角形ABC关于边BC镜像对称得到三角形A'BC，AO延长交三角形A'BC于点D'。不难看出D和D'也关于BC对称，所以有OD=OD'
那我们就可以以此类推把求折线段长度转化为求一条线段长度。即把图像沿对称边翻折一次后的新多边形内最长的一条线段。
假如说反弹多次呢？同理，但要注意的是只翻折上一次翻折得到的图形而不是新的大图形。
比如下图种光路为A->O->D->E

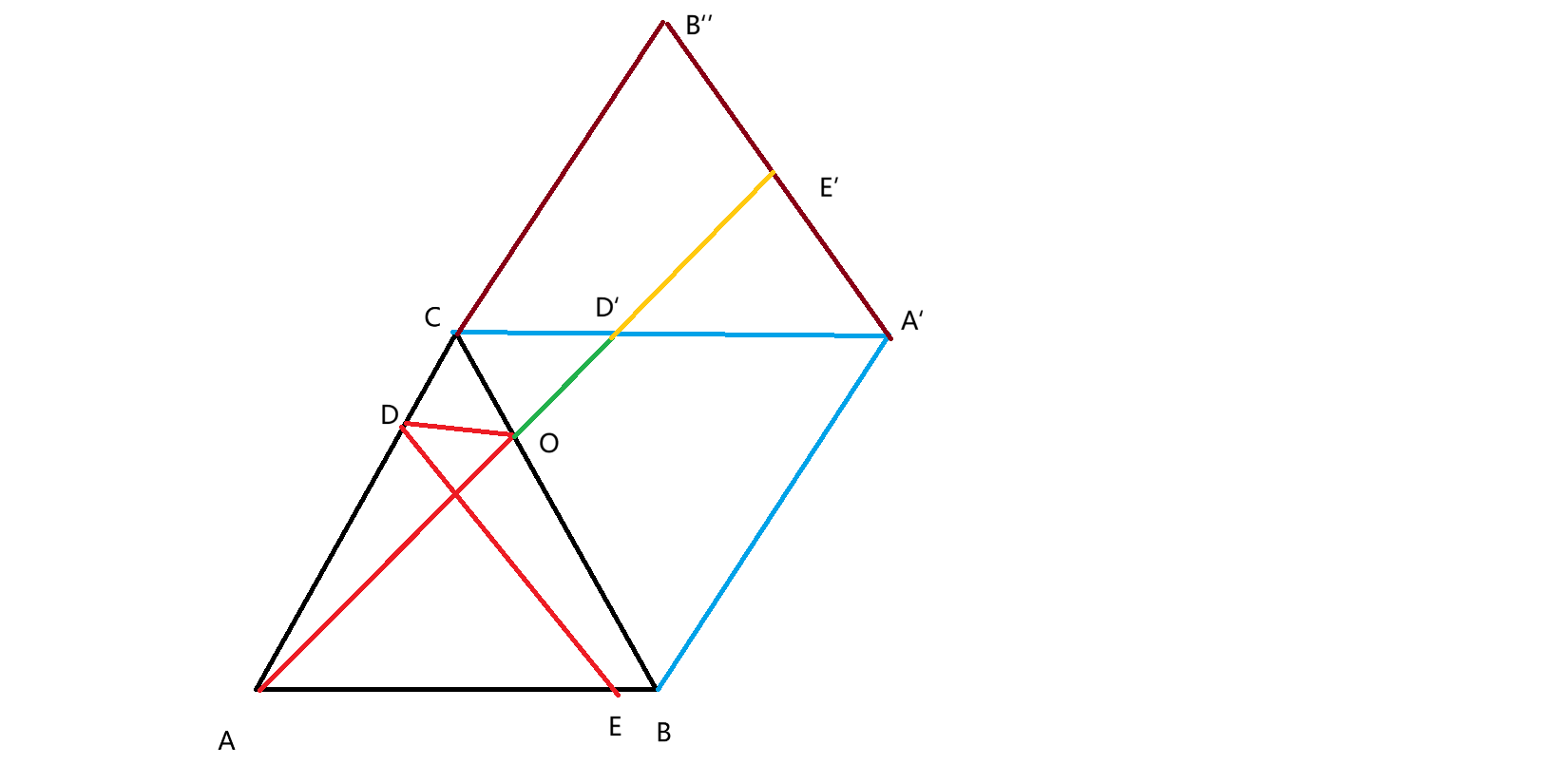
我们应该沿CA'翻转三角形A'BC而不是翻转四边形ABCA'
（其实B'C'分别和BC重合了更直观的可以把每第n次翻折后的三角形表示为An'Bn'Cn'）
那我们如何确定应该如何翻折多边形呢？
数据范围很小，我们可以使用dfs枚举每一次从哪条边反弹的序列，那每一次对称的对称边就是本次反弹的边。
于是乎我们来考虑得到这样一个翻折多次后的多边形如何求答案。
首先来判断什么样的直线是合法的。
我们不妨记第n次翻折的多边形为An，得到它的对称边为An的入边，从它得到An+1的边几座它的出边，A0没有入边,Ak没有出边（假设弹K次）
因为要满足反弹n次，所以这条线段必须要经过所有的对称边，其次这条线段应完全在多边形内，而因为An和An+1的重合边是对称边，其实满足前一个条件这个条件自然也满足了。
再来考虑什么时候直线被截的线段最长
我们不妨只考虑线段和其两端点所在的两边

考虑对红色边进行略微左旋右旋上下平移的操作，不难发现，总有一种情况会让线段变长。
所以我们不妨假设这条线段是被两个点卡住了以至于不能进行上述操作，这种情况才能是最优的。
那我们只用枚举所有在对称边上的点即可（直线不可能与多边形交于非对称边）
但是真的是这样吗？（其实官方题解也是单纯的这么想但是有问题）
我们来看下面这种情况

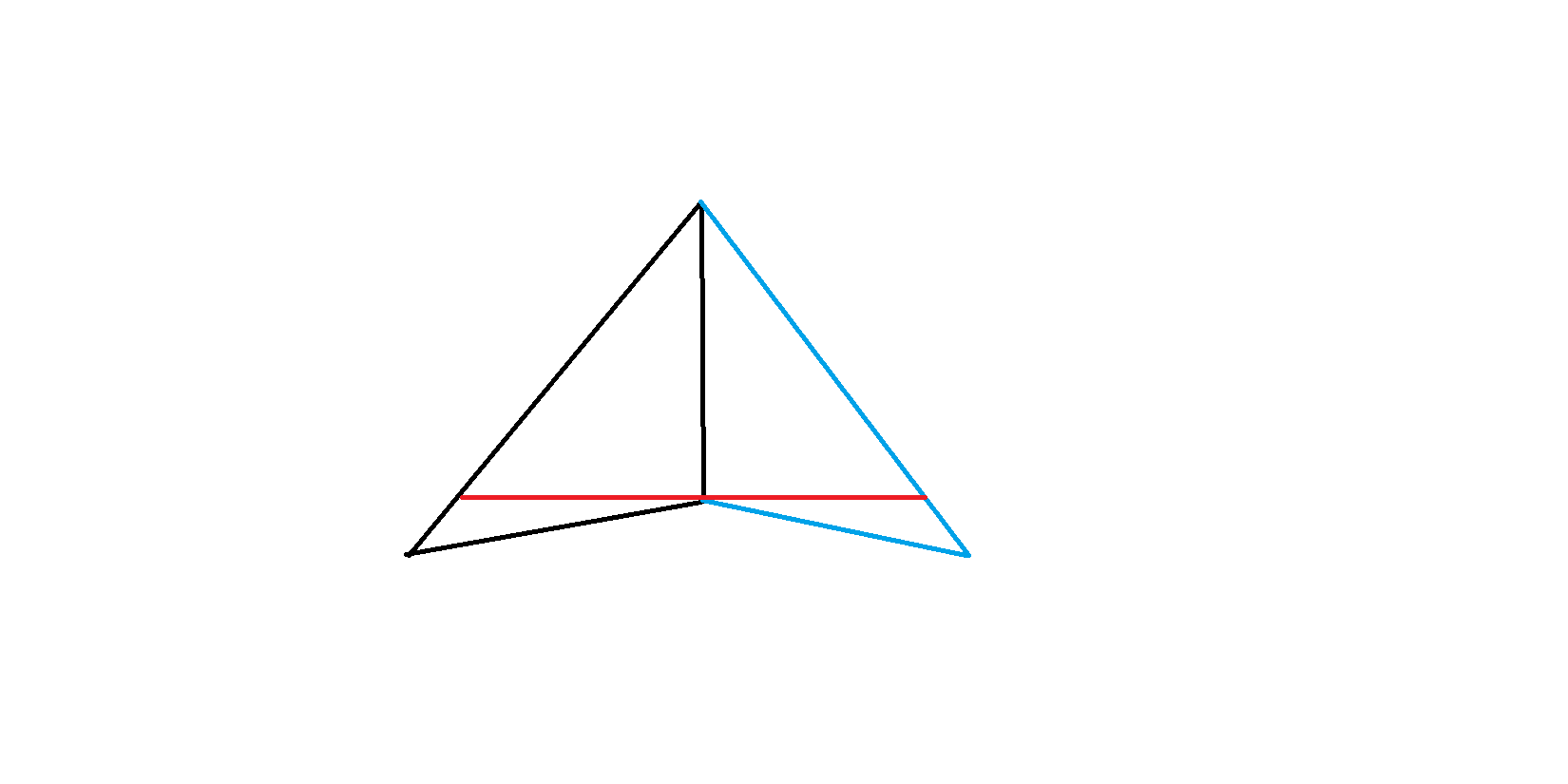
这是一个钝角三角形，沿一条短边对称答案显然在取红线的时候最优，但是它并没有被卡住。
这是为什么呢？因为对这条线段进行左旋右旋上下平移这四种操作中，左旋右旋此时由于对称性等价了都会使答案变小，而向下平移被一个点卡住了所以这条线段可以作为最优解。
为此我们需要特别考虑左旋右旋微扰等价的情况，不难想到必须要满足当前线段与左右两边夹角相同。此时可以枚举对称边的端点，然后再枚举A0和An的两条边算出此时应该有的斜率放入可能的直线集合中
（其实直接把斜率设成与端点所在对称边垂直就能过这个题了，可能是等价可能是数据水了（？））
剩下的操作就很简单了，我们只用实现一些基本函数就彳亍了
1.点关于点对称
这个拿笔算一算就好了
2.直线与直线求交点
联立求解即可
3.点关于直线l对称
先做一个过该点且垂直于直线l的直线l1,l交l1与p,让点关于p对称即可
4.判断直线与线段是否有交点
找出线段所在直线，两直线求交点，判断交点是否在线段上即可
5.求直线与多边形A0与Ak交点
我们似乎只需要考虑A0和Ak的非对称边的交点，枚举非对称边即可
真的吗？
其实不然，应该是先求出与对称边的交点，然后返回不是这个点的交点，因为直线可能刚好与对称边交于一个端点
其余的应该都很简单了不说了（
然后再说下一些注意事项，记得判断相等要改成绝对值之差小于eps,然后对原始数据进行微扰防止出现可能的直线与某条边重合的情况(但是不加也能过，疑似数据过水)
最容易忘记的，记得要把ans取max，因为题目说的是最多弹k次时候的最大值，不一定要弹到k次
代码不压行358行，还是有点恐怖的

using namespace std;
#define ld long double
const ld eps=1e-10;
const ld eps0=1e-12;
const ld INF=1e100;
struct point{
	ld x,y;
	point(ld X=INF,ld Y=INF)
	{
		x=X;
		y=Y;
	}
	const bool operator == (const point &p) const
	{
		return (p.x-x<=eps)&&(p.x-x)>=-eps&&(p.y-y)<=eps&&(p.y-y)>=-eps;
	}
	const bool operator != (const point &p) const
	{
		return p.x-x>eps||p.y-y>eps||x-p.x>eps||y-p.y>eps;
	}
	const bool operator > (const point &p) const
	{
		return abs(p.x-x)<=eps?y>p.y:x>p.x;
	}
	const bool operator < (const point &p) const
	{
		return abs(p.x-x)<=eps?y<p.y:x<p.x;
	}
};
struct line{
	ld k,b;
	line(ld K=INF,ld B=INF)
	{
		k=K,b=B;
	}
	const bool operator == (const line &l) const
	{
		return abs(k-l.k)<=eps&&abs(b-l.b)<=eps;
	}
};
struct seg{
	point p1,p2;
	const bool operator !=(const seg &s)
	{
		return !(p1==s.p1&&p2==s.p2)&&!(p2==s.p1&&p1==s.p2);
	}
};
point mirror(point a,point b)
{
	point c;
	c.x=((ld)2.0*b.x-a.x);
	c.y=((ld)2.0*b.y-a.y);
	//if(c.x+a.x!=2.0*b.x)
	return c;
}
ld get_dis(point a,point b)
{
	return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
ld get_k(point a,point b)
{
	if(a.x==b.x) return INF;
	return (a.y-b.y)/(a.x-b.x);
}
ld get_k(seg l)
{
	return get_k(l.p1,l.p2);
}
point get_point(line l1,line l2)
{
	if(l1.k==l2.k)
	{
		return point(INF,INF);
	}
	if(l1.k==INF)
	{
		return point(l1.b,l1.b*l2.k+l2.b);
	}
	else if(l2.k==INF)
	{
		return point(l2.b,l2.b*l1.k+l1.b);
	}
	else
	{
		return point(-(l2.b-l1.b)/(l2.k-l1.k),-l1.k*((l2.b-l1.b)/(l2.k-l1.k))+l1.b);
	}
}
point mirror(point a,line l)
{
	if(l.k==0)
	{
		return point(a.x,2.0*l.b-a.y);
	}
	else if(l.k==INF)
	{
		return point(2.0*l.b-a.x,a.y);
	}
	else
	{
		//cout<<get_point(l,line(-1.0/l.k,a.y+a.x/l.k)).x<<endl;
		return mirror(a,get_point(l,line(-1.0/l.k,a.y+a.x/l.k)));
	}
}
line to_line(seg s)
{
	if(s.p1.x==s.p2.x)
	{
		return line(INF,s.p1.x);
	}
	return line((s.p1.y-s.p2.y)/(s.p1.x-s.p2.x),-s.p1.x*(s.p1.y-s.p2.y)/(s.p1.x-s.p2.x)+s.p1.y);
}
line to_line(point p1,point p2)
{
	if(p1.x==p2.x)
	{
		return line(INF,p1.x);
	}
	return line((p1.y-p2.y)/(p1.x-p2.x),-p1.x*(p1.y-p2.y)/(p1.x-p2.x)+p1.y);
}
seg to_seg(point a,point b)
{
	seg s;
	s.p1=a,s.p2=b;
	return s;
}
point mirror(point a,seg s)
{
	return mirror(a,to_line(s));
}
bool on_seg(point p,seg s)
{
	if(p==s.p1||p==s.p2) return 1;
	return ((p.x-s.p1.x)*(p.x-s.p2.x)<=1e-4&&(p.y-s.p1.y)*(p.y-s.p2.y)<=1e-4);
}
point get_point(seg s,line l)
{
	line l2=to_line(s);
	point p=get_point(l,l2);
	if(on_seg(p,s))
	{
		return p;
	}
	return point(INF,INF);
}
int n,k;
struct node{
	point v[7];
	int in,out;
	node()
	{
		in=out=0;
		for(int i=0;i<=6;++i)
		v[i]=point();
	}
	seg get(int x)
	{
		if(x==0)
		{
			return seg();
		}
		if(x==n)
		{
			return to_seg(v[1],v[n]);
		}
		return to_seg(v[x],v[x+1]);
	}
}st;
point get_point(line l,node a)
{
	//cout<<a.in<<' '<<a.out<<endl;
	seg s=a.get(a.in==0?a.out:a.in);
	point ex=get_point(s,l);
	for(int i=1;i<=n;++i)
	{
		seg s=a.get(i);
		point p=get_point(s,l);
		if(p!=point()&&p!=ex)
		{
			//puts("ffffffff");
			return p;
		}
	}
	return point(INF,INF);
}
node lst[10];
int num[10];
ld ans[10];
bool check(line l)
{
	for(int i=1;i<=k;++i)
	{
		if(to_line(lst[i].get(lst[i].in))==l) continue;
		if(get_point(lst[i].get(lst[i].in),l)==point(INF,INF)) return 0;
	}
	return 1;
}
point pst[500];
int top;
void solve()
{
	//cout<<k<<endl;
	lst[0]=st;
	lst[0].out=num[1];
	for(int i=1;i<=k;++i)
	{
		for(int j=1;j<=n;++j)
		{
			lst[i].v[j]=mirror(lst[i-1].v[j],lst[i-1].get(num[i]));
		}
		lst[i].in=num[i];
		lst[i].out=num[i+1];
	}
	lst[k].out=0;
	lst[0].in=0;
	top=0;
	for(int i=1;i<=n;++i)
	{
		pst[++top]=lst[0].v[i];
	}
	for(int i=2;i<k;++i)
	{
		pst[++top]=lst[i].get(lst[i].in).p1;
		pst[++top]=lst[i].get(lst[i].in).p2;
	}
	for(int i=1;i<=n;++i)
	{
		pst[++top]=lst[k].v[i];
	}
	sort(pst+1,pst+1+top);
	top=unique(pst+1,pst+1+top)-pst-1;
	for(int i=1;i<=top;++i)
	{
		//printf("%Lf %Lf\n",pst[i].x,pst[i].y);
	}
	for(int i=1;i<=top;++i)
	{
		for(int j=i+1;j<=top;++j)
		{
			line l=to_line(pst[i],pst[j]);
			if(check(l))
			{
				point p1=get_point(l,lst[0]);
				point p2=get_point(l,lst[k]);
				if(p1!=point(INF,INF)&&p2!=point(INF,INF))
				{
					//printf("%Lf %Lf %Lf %Lf\n",p1.x,p1.y,p2.x,p2.y);
					ans[k]=max(ans[k],get_dis(p1,p2));
				}
				
			}
		}
	}
	for(int i=1;i<=k;++i)
	{
		line l=to_line(lst[i].get(lst[i].in));
		line l0;
		if(l.k==INF)
		{
			l0.k=0;
			l0.b=lst[i].get(lst[i].in).p1.x;
		}
		else if(l.k==0)
		{
			l0.k=INF;
			l0.b=lst[i].get(lst[i].in).p1.y;
		}
		else
		{
			l0.k=-1.0/l.k;
			l0.b=-l0.k*lst[i].get(lst[i].in).p1.x+lst[i].get(lst[i].in).p1.y;
		}
		//cout<<l0.k<<' '<<l0.b<<endl;
		if(check(l0))
		{
			point p1=get_point(l0,lst[0]);
			point p2=get_point(l0,lst[k]);
			if(p1!=point(INF,INF)&&p2!=point(INF,INF))
			{
				//printf("%Lf %Lf %Lf %Lf\n",p1.x,p1.y,p2.x,p2.y);
				ans[k]=max(ans[k],get_dis(p1,p2));
			}	
		}
		if(l.k==INF)
		{
			l0.k=0;
			l0.b=lst[i].get(lst[i].in).p2.x;
		}
		else if(l.k==0)
		{
			l0.k=INF;
			l0.b=lst[i].get(lst[i].in).p2.y;
		}
		else
		{
			l0.k=-1.0/l.k;
			l0.b=-l0.k*lst[i].get(lst[i].in).p2.x+lst[i].get(lst[i].in).p2.y;
		}
		//cout<<l0.k<<' '<<l0.b<<endl;
		if(check(l0))
		{
			point p1=get_point(l0,lst[0]);
			point p2=get_point(l0,lst[k]);
			if(p1!=point(INF,INF)&&p2!=point(INF,INF))
			{
				//printf("%Lf %Lf %Lf %Lf\n",p1.x,p1.y,p2.x,p2.y);
				ans[k]=max(ans[k],get_dis(p1,p2));
			}	
		}
	}
}
bool vis[10];
void dfs(int dep,int f)
{
	if(dep>k)
	{
		solve();
		return ;
	}
	for(int i=1;i<=n;++i)
	{
		if(i==f||vis[i]) continue;
		num[dep]=i;
		vis[i]=1;
		dfs(dep+1,i);
		vis[i]=0;
	}
}
int main()
{
//	point p=mirror(point(4,0),line(-3.0/4.0,3));
//	printf("%Lf %Lf\n",p.x,p.y);
	//cout<<get_dis(point(-86.000000,12.000000),point(-60.550296,1.520710))<<endl;
	cin>>n;
	for(int i=1;i<=n;++i)
	{
		point a;
		cin>>a.x>>a.y;
		a.x+=eps0*(ld)i;
		a.y-=eps0*(ld)i;
		st.v[i]=a;
	}
	for(int i=1;i<=n;++i)
	{
		for(int j=i+1;j<=n;++j)
		{
			ans[0]=max(ans[0],get_dis(st.v[i],st.v[j]));
		}
	}
	printf("%.18Lf\n",ans[0]);
	for(int i=1;i<=n;++i)
	{
		k=i;
		dfs(1,0);
		ans[i]=max(ans[i],ans[i-1]);
		printf("%.18Lf\n",ans[i]);
	}
}```