求斐波拉契数列第n位算法优化
在面试题中经常遇到求斐波拉契数列值的问题,最常见算法是使用递归的方式,本篇博客介绍如何优化该算法性能。
斐波拉契数列的特性是:n=(n-2)+(n-1)
首先使用递归的方式求斐波拉契数列第30位:
static void Main(string[] args)
{
Stopwatch sw = new Stopwatch();
sw.Start();
Console.WriteLine(Fun(30));
sw.Stop();
Console.WriteLine("总运行时间:" + sw.Elapsed);
Console.WriteLine("测量实例得出的总运行时间(毫秒为单位):" + sw.ElapsedMilliseconds);
Console.WriteLine("总运行时间(计时器刻度标识):" + sw.ElapsedTicks);
Console.WriteLine("计时器是否运行:" + sw.IsRunning.ToString());
}
public static int Fun(int n)
{
if (n == 1 || n == 2)
{
return 1;
}
return Fun(n - 2) + Fun(n - 1);
}
执行结果:
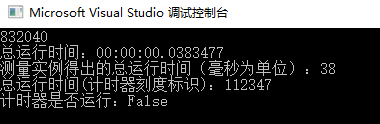
递归的方式致使 Fun() 方法被多次重复调用,此时的空间复杂度为 O(n),时间复杂度为 O(2ⁿ),n的值越大,时间复杂度也就越大。为避免Fun() 被多次重复调用,减小时间复杂度,我们可以用数组来存储计算出来的数据。
public static int Fun(int n)
{
int[] array = new int[n];
array[0] = 1;
array[1] = 1;
for (int i = 2; i < n; i++)
{
array[i] = array[i - 2] + array[i - 1];
}
return array[n - 1];
}
执行结果:
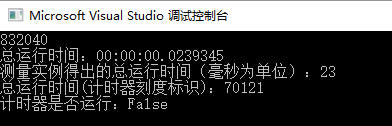
运行程序时间比递归方式的小,效率明显提升,此时时间复杂度为 O(n),空间复杂度为 O(n),但是我们发现,在计算n的值时,我们只需最新的三个数,前面的数就不需要了,那么我们可以定义三个常量来减少空间复杂度。
public static int Fun(int n)
{
int first = 1;
int second = 1;
int third = 2;
for (int i = 3; i <= n; i++)
{
third = first + second;
first = second;
second = third;
}
return third;
}
执行结果:
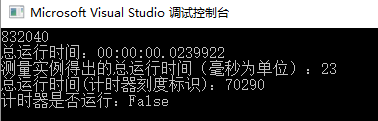
此时程序运行时间和上个方法相差无几,但是此时的空间复杂度从 O(n) 变成了0,时间复杂度为 O(n),所以这种方式是非常高效的。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号