算法day36 二叉树的前中后序的非递归实现

题目描述

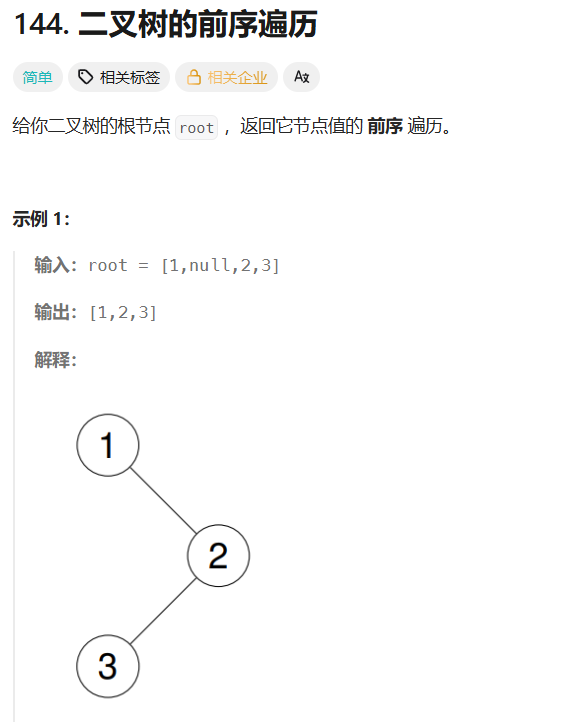
思路：栈
由于前序的序列为根左右，那么我们这里的操作就是先以右子树入栈，随后左子树入栈，这样根据栈的性质，出栈时就能得到左在前，右在后的效果，具体的代码实现如下.

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> res;
        TreeNode *temp;
        st.push(root);
        while(!st.empty()){
            temp = st.top();
            st.pop();
            if(temp){
                res.push_back(temp->val);
            }else{
                continue;
            }
            st.push(temp->right);
            st.push(temp->left);
        }

        return res;
    }
};

思路：栈
中序的思路整体与前序差不多，关键在于，要符合中序的顺序即左根右，具体代码如下。

class Solution {
    public:
        vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
            stack<TreeNode*> st;
            //先压栈保证栈非空从而进入循环
            if(root) st.push(root);
            while( !st.empty()){
                TreeNode *cur = st.top();
                //如果当前的栈顶不是空，那么我们将它弹出，并按照右根左压栈（这样出栈时形成左根右的顺序）
                if(cur){
                     st.pop();
                    if(cur->right) st.push(cur->right);
                    st.push(cur);
                    st.push(nullptr);
                    if(cur->left) st.push(cur->left);
                }else{
                    //到这里说明 cur == nullptr
                    //回退到父节点
                    //弹出空节点
                    st.pop();
                    cur = st.top(); 
                    st.pop();
                    res.push_back(cur->val);
                }
              }

            return res;
        }
    };

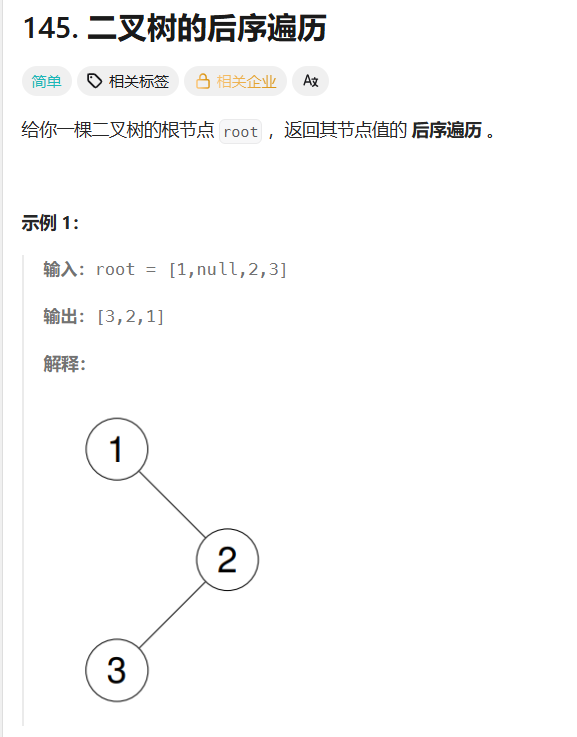
思路：栈
后序整体与前序非常接近，由于后序的规则是左右跟，那么我们只需要调整一下前序中的压栈顺序，并将输出的数组进行逆序，便得到了对应的后序序列,代码如下。

class Solution {
    public:
         vector<int> postorderTraversal(TreeNode* root) {
         stack<TreeNode*> st;
         vector<int> res;
         TreeNode *temp;
         st.push(root);
         while(!st.empty()){
            temp = st.top();
            st.pop();
            if(temp){
                res.push_back(temp->val);
            }else{
                continue;
            }
            st.push(temp->left);
            st.push(temp->right);
        }
        reverse(res.begin(),res.end());
        return res;
    }
 };

以上代码的时间复杂度均为O(n)
以上代码的空间复杂度均为O(n)

END