算法day6 区间和

题目描述

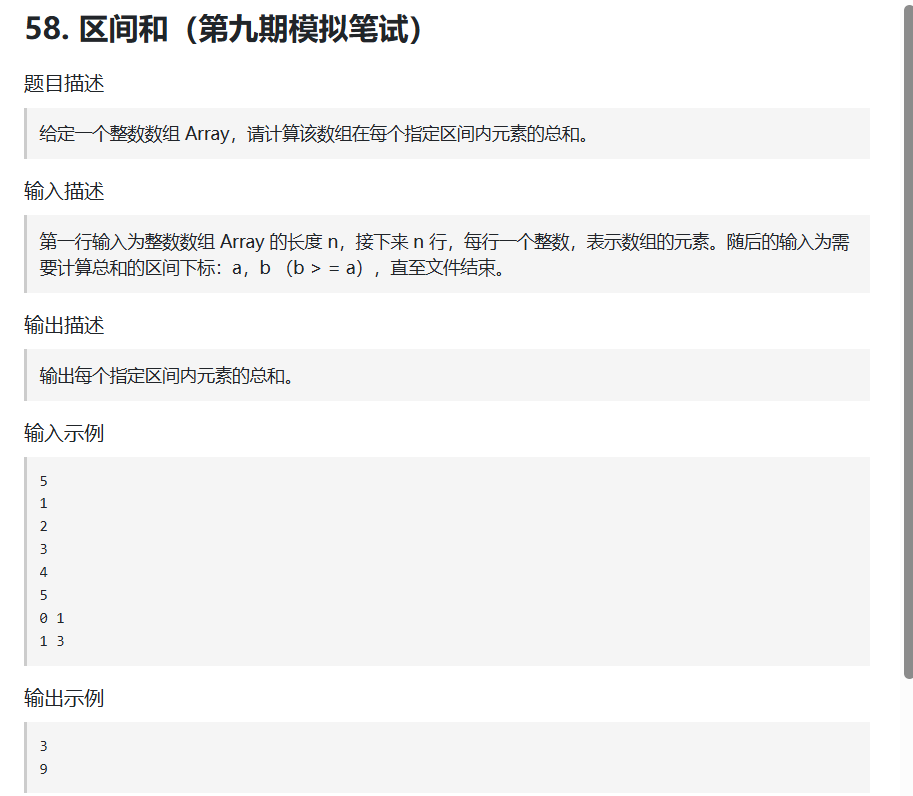
思路
这道题目求区间和，如果在数据规模很低的情况下，我们可以直接for循环遍历所属区间然后求和返回即可，但是考虑到在大规模数据引入的情况下，如果区间的范围很大，则会有比较差的性能表现，所以我们主要介绍采用前缀和求解的方法。前缀和即随着位置后移不断累加当前即之前位置元素之和得到的对应位置的和，他相较于遍历的优点是我们在初始化阶段便已经求得各个位置的前缀和，那么区间和只需要区间尾前缀和减去区间首前缀和即可求得区间的和。这样只在O(1)的消耗下便完成了操作。

代码如下

  #include <iostream>
  #include <vector>

  using namespace std;

  int main(){
    int n;
    int presum = 0;
    scanf("%d",&n);
    vector<int> nums(n);
    vector<int> psum(n);
    for(int i=0;i<n;i++){
       scanf("%d",&nums[i]);
       presum += nums[i]; //presum动态更新，随着循环不断的更新各个位置的前缀和
       psum[i] = presum;
  }
    int begin,end;
    while(cin>>begin>>end){
       printf("%d\n",psum[end]-psum[begin-1]); //这里要注意求begin至end区间和时，减去的前缀和应该是psum[begin-1]，因为区间和的区间是闭合的。
 }

    return 0;
}

时间复杂度：O(n)
空间复杂度：O(n)

END