1053 Path of Equal Weight——PAT甲级真题
1053 Path of Equal Weight
给定一个非空的树，树根为 RR。
树中每个节点 TiTi 的权重为 WiWi。
从 RR 到 LL 的路径权重定义为从根节点 RR 到任何叶节点 LL 的路径中包含的所有节点的权重之和。
现在给定一个加权树以及一个给定权重数字，请你找出树中所有的权重等于该数字的路径（必须从根节点到叶节点）。
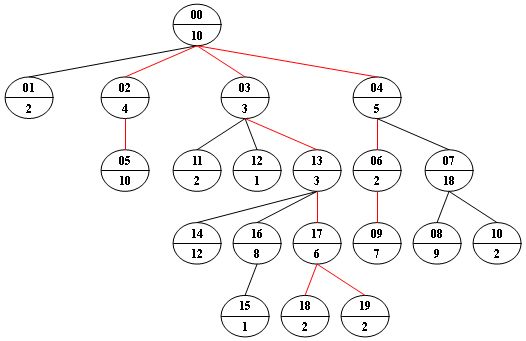
例如，我们考虑下图的树，对于每个节点，上方的数字是节点
ID，它是两位数字，而下方的数字是该节点的权重。假设给定数为 2424，则存在 44 个具有相同给定权重的不同路径：
{10 5 2 7}，{10 4 10}，{10 3 3 6 2}，{10 3 3 6 2}， 已经在图中用红色标出。
输入格式
第一行包含三个整数 N,M,SN,M,S，分别表示树的总节点数量，非叶子节点数量，给定权重数字。
第二行包含 NN 个整数 WiWi，表示每个节点的权重。
接下来 MM 行，每行的格式为：
ID K ID[1] ID[2] ... ID[K]IDID 是一个两位数字，表示一个非叶子结点编号，KK 是一个整数，表示它的子结点数，接下来的 KK 个 ID[i]ID[i] 也是两位数字，表示一个子结点的编号。
出于方便考虑，根节点固定为 0000，且树中所有节点的编号为 00∼N−100∼N−1。
输出格式
以单调递减的顺序输出所有权重为S的路径。
每个路径占一行，从根节点到叶节点按顺序输出每个节点的权重。
注意：我们称 AA 序列 {A1,A2,…,An}{A1,A2,…,An} 大于 BB 序列 {B1,B2,…,Bm}{B1,B2,…,Bm}，当且仅当存在一个整数 kk，1≤k<min(n,m)1≤k<min(n,m)，对于所有 1≤i≤k1≤i≤k，Ai=BiAi=Bi 成立，并且 Ak+1>Bk+1Ak+1>Bk+1。
数据范围
1≤N≤1001≤N≤100,
0≤M<N0≤M<N,
0<S<2300<S<230,
0<Wi<10000<Wi<1000输入样例：
20 9 24 10 2 4 3 5 10 2 18 9 7 2 2 1 3 12 1 8 6 2 2 00 4 01 02 03 04 02 1 05 04 2 06 07 03 3 11 12 13 06 1 09 07 2 08 10 16 1 15 13 3 14 16 17 17 2 18 19输出样例：
10 5 2 7 10 4 10 10 3 3 6 2 10 3 3 6 2
题目大意：给你一棵树，让你从叶节点到根节点的权值之和等于S的路径。
大致思路：题目要求我们输出的时候要按照结点权值由大到小输出，所以在读入每个节点的孩子结点的时候，把每个结点的孩子结点按照权值的大小由大到小排序。同时我们还要定义一个path数组用来记录搜索路径。最后进行DFS。
代码：
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
struct node {
long long val; //每个结点的权重
vector<int> child;
long long weight; //记录每个结点的权重
} root[N];
long long n, m, s;
vector<int> path;
bool vis[N]; //标记当前结点有没有访问过
int cnt = 0;
void DFS(int x) {
if (root[x].child.size() == 0) {
if (root[x].weight == s) {
// cout << "叶子结点为：" << x << endl;
// cout << "结点权值是：" << root[x].weight << endl;
for (int i = 0; i < path.size(); i++) {
cout << root[path[i]].val;
if (i != path.size() - 1)
cout << " ";
else
cout << endl;
}
return;
}
return;
}
for (int i = 0; i < root[x].child.size(); i++) {
int tmp = root[x].child[i];
int w = root[tmp].weight;
if (!vis[tmp]) {
vis[tmp] = true;
root[tmp].weight += root[x].weight;
path.push_back(tmp);
DFS(tmp);
vis[tmp] = false;
root[tmp].weight = w; //回溯
path.pop_back();
}
}
}
bool cmp(int a, int b) { return root[a].weight > root[b].weight; }
int main() {
memset(vis, 0, sizeof(vis));
cin >> n >> m >> s;
for (int i = 0; i < n; i++) {
scanf("%lld", &root[i].val);
root[i].weight = root[i].val;
}
for (int i = 0; i < m; i++) {
int id, k;
cin >> id >> k;
for (int j = 0; j < k; j++) {
int x;
cin >> x;
root[id].child.push_back(x);
}
sort(root[id].child.begin(), root[id].child.end(), cmp);
}
path.push_back(0);
DFS(0);
return 0;
}
