CF2094E Boneca Ambalabu（异或）

CF2094E Boneca Ambalabu

题目描述

Boneca Ambalabu gives you a sequence of $ n $ integers $ a_1,a_2,\ldots,a_n $ .

Output the maximum value of $ (a_k\oplus a_1)+(a_k\oplus a_2)+\ldots+(a_k\oplus a_n) $ among all $ 1 \leq k \leq n $ . Note that $ \oplus $ denotes the bitwise XOR operation.

输入格式

The first line contains an integer $ t $ ( $ 1 \leq t \leq 10^4 $ ) – the number of independent test cases.

The first line of each test case contains an integer $ n $ ( $ 1 \leq n\leq 2\cdot 10^5 $ ) – the length of the array.

The second line of each test case contains $ n $ integers $ a_1,a_2,\ldots,a_n $ ( $ 0 \leq a_i < 2^{30} $ ).

It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 2\cdot 10^5 $ .

输出格式

For each test case, output the maximum value on a new line.

输入输出样例 #1

输入 #1

5
3
18 18 18
5
1 2 4 8 16
5
8 13 4 5 15
6
625 676 729 784 841 900
1
1

输出 #1

0
79
37
1555
0

说明/提示

In the first test case, the best we can do is $ (18\oplus18)+(18\oplus18)+(18\oplus18)=0 $ .

In the second test case, we choose $ k=5 $ to get $ (16\oplus1)+(16\oplus2)+(16\oplus4)+(16\oplus8)+(16\oplus16)=79 $ .
异或运算的每一位是独立的，总和的每一位贡献可以分开计算。

异或运算的位独立性与总和分解

核心概念

异或运算的每一位是独立的，这意味着每一位的结果只与当前位的值相关，与其他位无关。因此，在计算异或总和时，可以将每一位的贡献分开计算，最后将所有位的贡献相加得到总和。

---

举例说明

假设数组为 [3, 5, 6]，其二进制表示为：

• 3 → 011
• 5 → 101
• 6 → 110

我们需要计算每个元素与其他元素的异或总和，并找到最大值。

---

1. 逐位统计贡献

对于每个二进制位 j，统计数组中该位为 1 的元素数量：

• 第0位（1的位）：3(1), 5(1), 6(0) → cnt[0] = 2
• 第1位（2的位）：3(1), 5(0), 6(1) → cnt[1] = 2
• 第2位（4的位）：3(0), 5(1), 6(1) → cnt[2] = 2

---

2. 计算每个元素的异或总和

以元素 3（二进制 011）为例：

• 第0位（值为1）：元素3的第0位是 1。
  • 其他元素中该位为 0 的数量为 n - cnt[0] = 3 - 2 = 1。
  • 贡献：1 * (1 << 0) = 1 * 1 = 1。
• 第1位（值为2）：元素3的第1位是 1。
  • 其他元素中该位为 0 的数量为 n - cnt[1] = 3 - 2 = 1。
  • 贡献：1 * (1 << 1) = 1 * 2 = 2。
• 第2位（值为4）：元素3的第2位是 0。
  • 其他元素中该位为 1 的数量为 cnt[2] = 2。
  • 贡献：2 * (1 << 2) = 2 * 4 = 8。
• 总和：1 + 2 + 8 = 11。

验证实际异或结果：

• 3^3 = 0、3^5 = 6、3^6 = 5。
• 总和：0 + 6 + 5 = 11，与计算结果一致。

---

3. 为什么可以分开计算？

• 异或的独立性：每个二进制位的异或结果仅取决于当前位的值，与其他位无关。
  • 例如，计算第2位的贡献时，无需关心第0位或第1位的值。
• 权值不重叠：每一位的权值（如 2^0, 2^1, 2^2）是独立的，总和可以通过直接相加得到。

---

总结

通过将每个二进制位的贡献独立计算，再累加所有位的贡献，可以高效地解决大规模异或总和问题。这种方法的优势在于：

1. 时间复杂度优化：从暴力法的 O(n²) 降为 O(n * log(max_value))。
2. 逻辑清晰：按位处理，避免了复杂的整体计算。
   

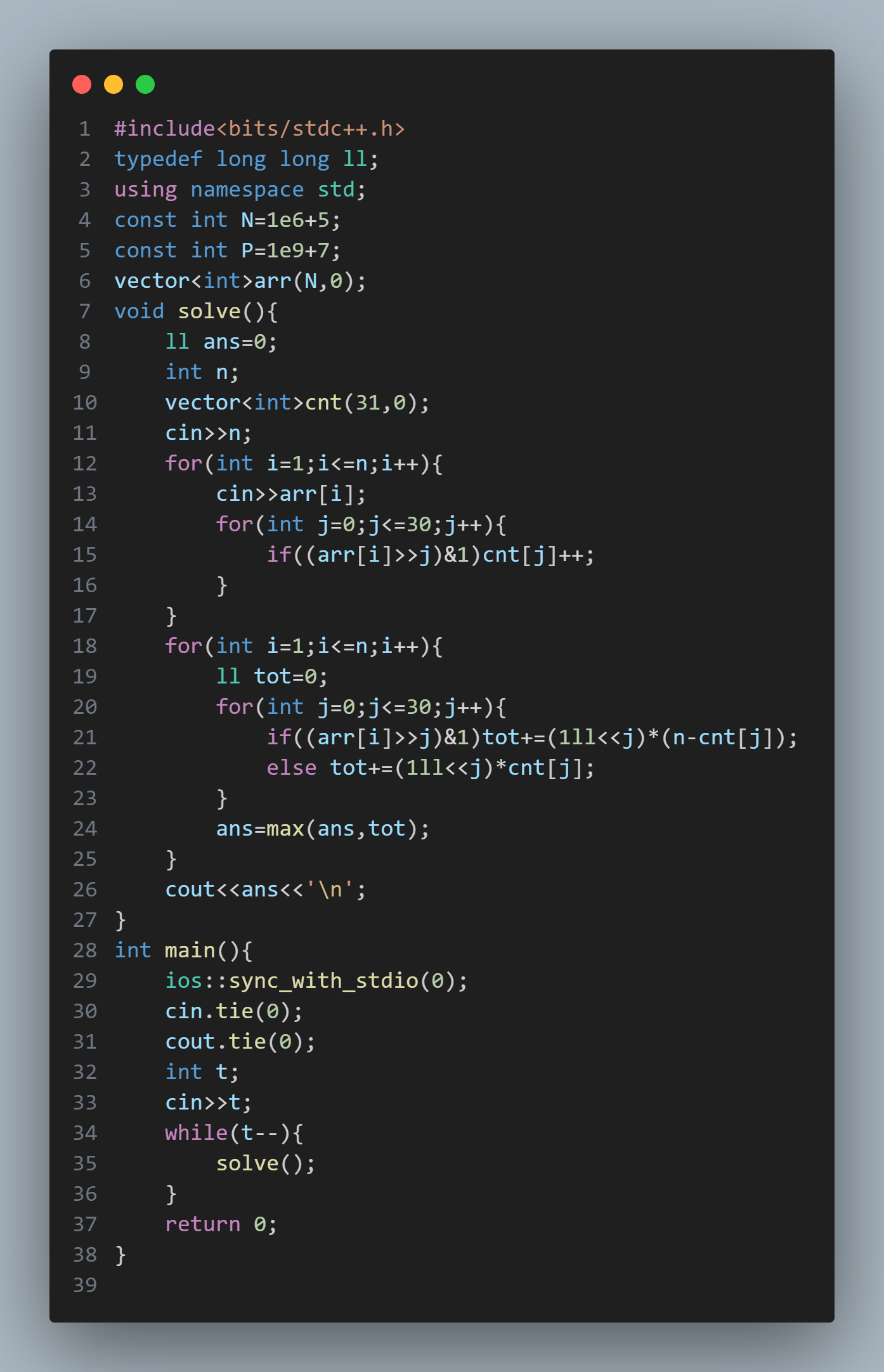
include<bits/stdc++.h>

typedef long long ll;
using namespace std;
const int N=1e6+5;
const int P=1e9+7;
vectorarr(N,0);
void solve(){
ll ans=0;
int n;
vectorcnt(31,0);
cin>>n;
for(int i=1;i<=n;i++){
cin>>arr[i];
for(int j=0;j<=30;j++){
if((arr[i]>>j)&1)cnt[j]++;
}
}
for(int i=1;i<=n;i++){
ll tot=0;
for(int j=0;j<=30;j++){
if((arr[i]>>j)&1)tot+=(1ll<<j)(n-cnt[j]);
else tot+=(1ll<<j)cnt[j];
}
ans=max(ans,tot);
}
cout<<ans<<'\n';
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
cin>>t;
while(t--){
solve();
}
return 0;
}