P2015 二叉苹果树（树上背包）

P2015 二叉苹果树

题目描述

有一棵苹果树，如果树枝有分叉，一定是分二叉（就是说没有只有一个儿子的结点）

这棵树共有 \(N\) 个结点（叶子点或者树枝分叉点），编号为 \(1 \sim N\)，树根编号一定是 \(1\)。

我们用一根树枝两端连接的结点的编号来描述一根树枝的位置。下面是一颗有 \(4\) 个树枝的树：

2   5
 \ / 
  3   4
   \ /
    1

现在这颗树枝条太多了，需要剪枝。但是一些树枝上长有苹果。

给定需要保留的树枝数量，求出最多能留住多少苹果。

输入格式

第一行 \(2\) 个整数 \(N\) 和 \(Q\)，分别表示表示树的结点数，和要保留的树枝数量。

接下来 \(N-1\) 行，每行 \(3\) 个整数，描述一根树枝的信息：前 \(2\) 个数是它连接的结点的编号，第 \(3\) 个数是这根树枝上苹果的数量。

输出格式

一个数，最多能留住的苹果的数量。

输入输出样例 #1

输入 #1

5 2
1 3 1
1 4 10
2 3 20
3 5 20

输出 #1

21

说明/提示

\(1 \leqslant Q < N \leqslant 100\)，每根树枝上的苹果 \(\leqslant 3 \times 10^4\)。

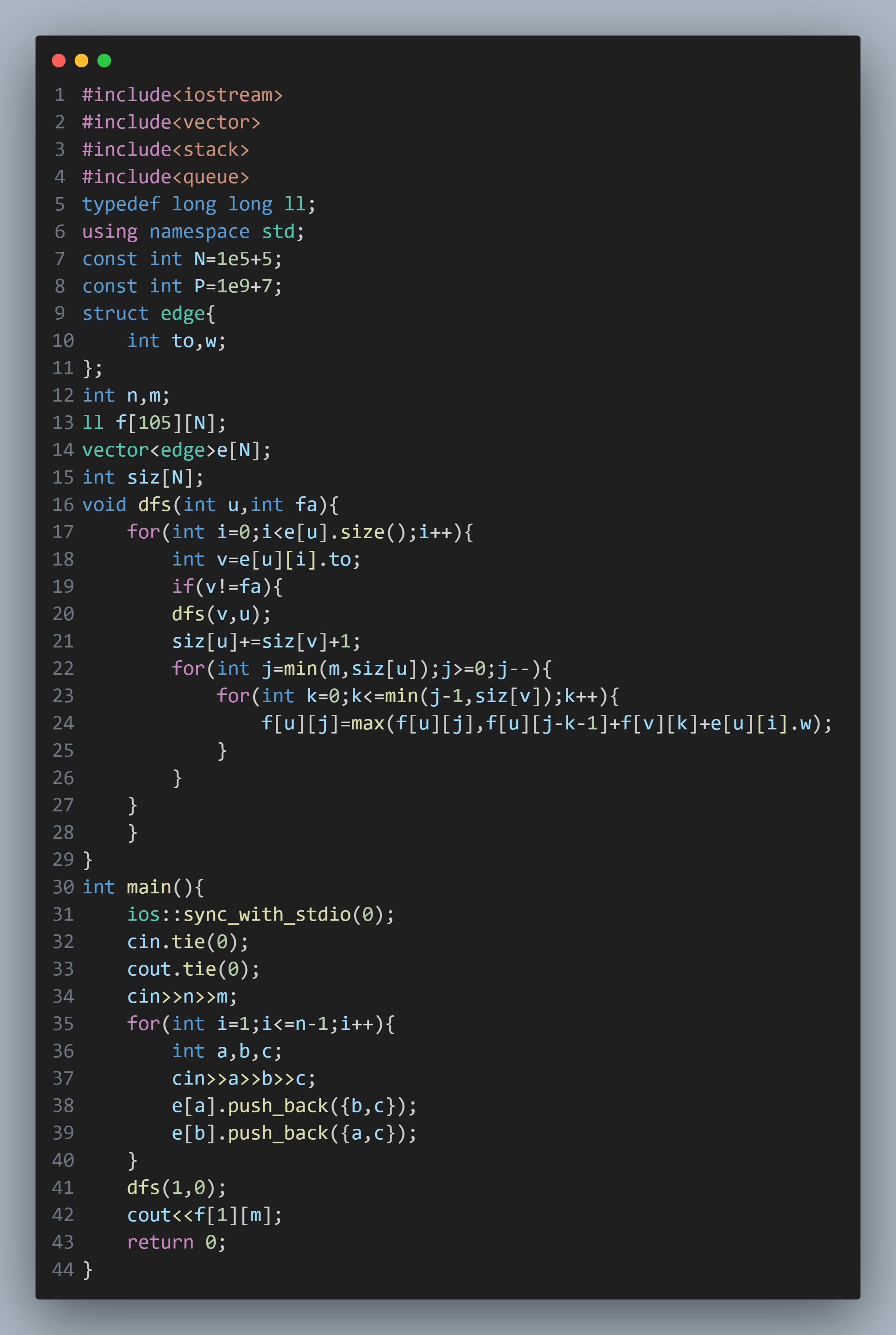
include

include

include

include

typedef long long ll;
using namespace std;
const int N=1e5+5;
const int P=1e9+7;
struct edge{
int to,w;
};
int n,m;
ll f[105][N];
vectore[N];
int siz[N];
void dfs(int u,int fa){
for(int i=0;i<e[u].size();i++){
int v=e[u][i].to;
if(v!=fa){
dfs(v,u);
siz[u]+=siz[v]+1;
for(int j=min(m,siz[u]);j>=0;j--){
for(int k=0;k<=min(j-1,siz[v]);k++){
f[u][j]=max(f[u][j],f[u][j-k-1]+f[v][k]+e[u][i].w);
}
}
}
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n-1;i++){
int a,b,c;
cin>>a>>b>>c;
e[a].push_back({b,c});
e[b].push_back({a,c});
}
dfs(1,0);
cout<<f[1][m];
return 0;
}