图论（连通分量）

AT_abc284_c [ABC284C] Count Connected Components

题目描述

頂点に $ 1 $ から $ N $ の番号が、辺に $ 1 $ から $ M $ の番号がついた $ N $ 頂点 $ M $ 辺の単純無向グラフが与えられます。辺 $ i $ は頂点 $ u_i $ と頂点 $ v_i $ を結んでいます。
グラフに含まれる連結成分の個数を求めてください。

输入格式

入力は以下の形式で標準入力から与えられる。

$ N $ $ M $ $ u_1 $ $ v_1 $ $ u_2 $ $ v_2 $ $ \vdots $ $ u_M $ $ v_M $

输出格式

答えを出力せよ。

输入输出样例 #1

输入 #1

5 3
1 2
1 3
4 5

输出 #1

2

输入输出样例 #2

输入 #2

5 0

输出 #2

5

输入输出样例 #3

输入 #3

4 6
1 2
1 3
1 4
2 3
2 4
3 4

输出 #3

1

说明/提示

注釈

単純無向グラフ とは、単純で辺に向きの無いグラフのことをいいます。
グラフが 単純 であるとは、グラフが自己ループや多重辺を含まないことをいいます。

あるグラフの 部分グラフ とは、元のグラフのいくつかの頂点といくつかの辺を選んでできるグラフのことをいいます。
グラフが 連結 であるとは、グラフに含まれるすべての頂点同士が辺を経由して互いに行き来できることをいいます。
連結成分 とは、連結な部分グラフのうち、そのグラフを含んだより大きい連結な部分グラフが存在しないものをいいます。

制約

• $ 1\ \leq\ N\ \leq\ 100 $
• $ 0\ \leq\ M\ \leq\ \frac{N(N\ -\ 1)}{2} $
• $ 1\ \leq\ u_i,\ v_i\ \leq\ N $
• 入力で与えられるグラフは単純
• 入力される値はすべて整数

Sample Explanation 1

与えられるグラフに含まれる連結成分は次の $ 2 $ 個です。 - 頂点 $ 1,\ 2,\ 3 $ および辺 $ 1,\ 2 $ からなる部分グラフ - 頂点 $ 4,\ 5 $ および辺 $ 3 $ からなる部分グラフ 
这道题本质上是求有几个连通分量，与强连通不同的是，这道题是求几个点在一起，比如说a到b，b到c，这个很明显没有形成一个环，但要视为一个连通分量，我们可以用dfs做，如果说一个点可以在遍历其他点的时候被遍历到就说明他们是一起的，比如说遍历a时b和c会一同遍历到，这时候我们可以从一遍历所有点，如果他没有在遍历其他点的时候被遍历，说明他属于一个新的集合，所以ans++；

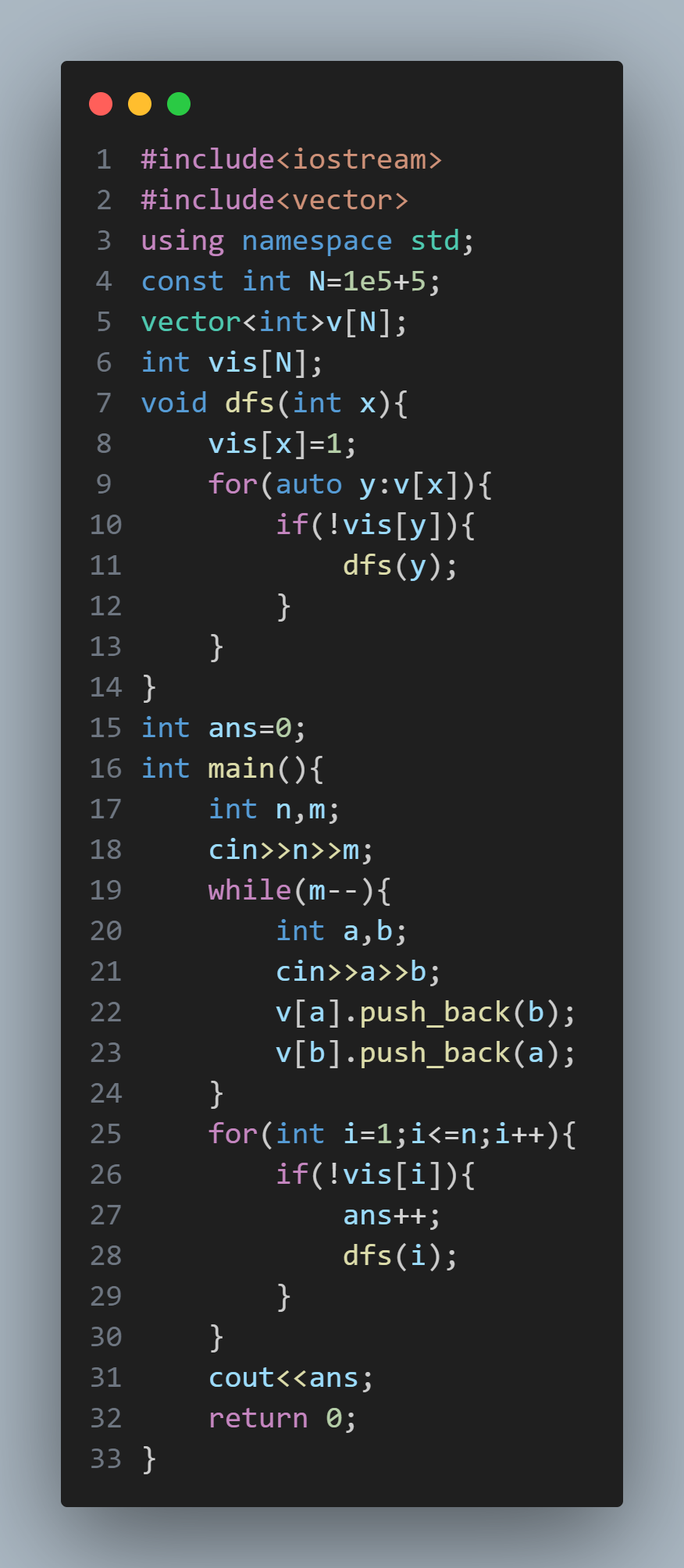
#include<iostream>
#include<vector>
using namespace std;
const int N=1e5+5;
vector<int>v[N];
int vis[N];
void dfs(int x){
    vis[x]=1;
    for(auto y:v[x]){
        if(!vis[y]){
            dfs(y);
        }
    }
}
int ans=0;
int main(){
    int n,m;
    cin>>n>>m;
    while(m--){
        int a,b;
        cin>>a>>b;
        v[a].push_back(b);
        v[b].push_back(a);
    }
    for(int i=1;i<=n;i++){
        if(!vis[i]){
            ans++;
            dfs(i);
        }
    }
    cout<<ans;
    return 0;
}