图论（连通性）

AT_abc399_c [ABC399C] Make it Forest

题目描述

给定一个由 \(N\) 个顶点和 \(M\) 条边构成的简单无向图，顶点编号为 \(1\) 至 \(N\)。第 \(i\) 条边连接顶点 \(u_i\) 和顶点 \(v_i\)。
若要将该图变为森林，至少需要删除多少条边？

森林的定义：简单无向图 \(F\) 是森林，当且仅当 \(F\) 不包含任何环。

输入格式

输入通过标准输入给出，格式如下：

\(N\) \(M\)
\(u_1\) \(v_1\)
\(u_2\) \(v_2\)
\(\vdots\)
\(u_M\) \(v_M\)

输出格式

输出答案。

输入输出样例 #1

输入 #1

4 4
1 2
1 3
2 4
3 4

输出 #1

1

输入输出样例 #2

输入 #2

5 0

输出 #2

0

输入输出样例 #3

输入 #3

10 10
7 9
4 6
6 10
2 5
5 6
5 9
6 8
4 8
1 5
1 4

输出 #3

2

说明/提示

约束条件

• \(1 \leq N \leq 2 \times 10^5\)
• \(0 \leq M \leq \min\left( \frac{N(N-1)}{2}, 2 \times 10^5 \right)\)
• \(1 \leq u_i < v_i \leq N\)
• 输入的图是简单无向图（无自环和重边）
• 所有输入值均为整数

样例解释 1

例如，删除第 1 条边后，该图将变为森林。

翻译由 DeepSeek R1 完成
这道题本质上是要求一个无向图中有几个环，这道题可以用并查集做，如果两条边的的端点的父节点是一样的，说明如果加上这条边就会形成个环，所以不能要这条边
![](https://img2024.cnblogs.com/blog/3599636/202503/3599636-20250331211151574-
175543493.png)

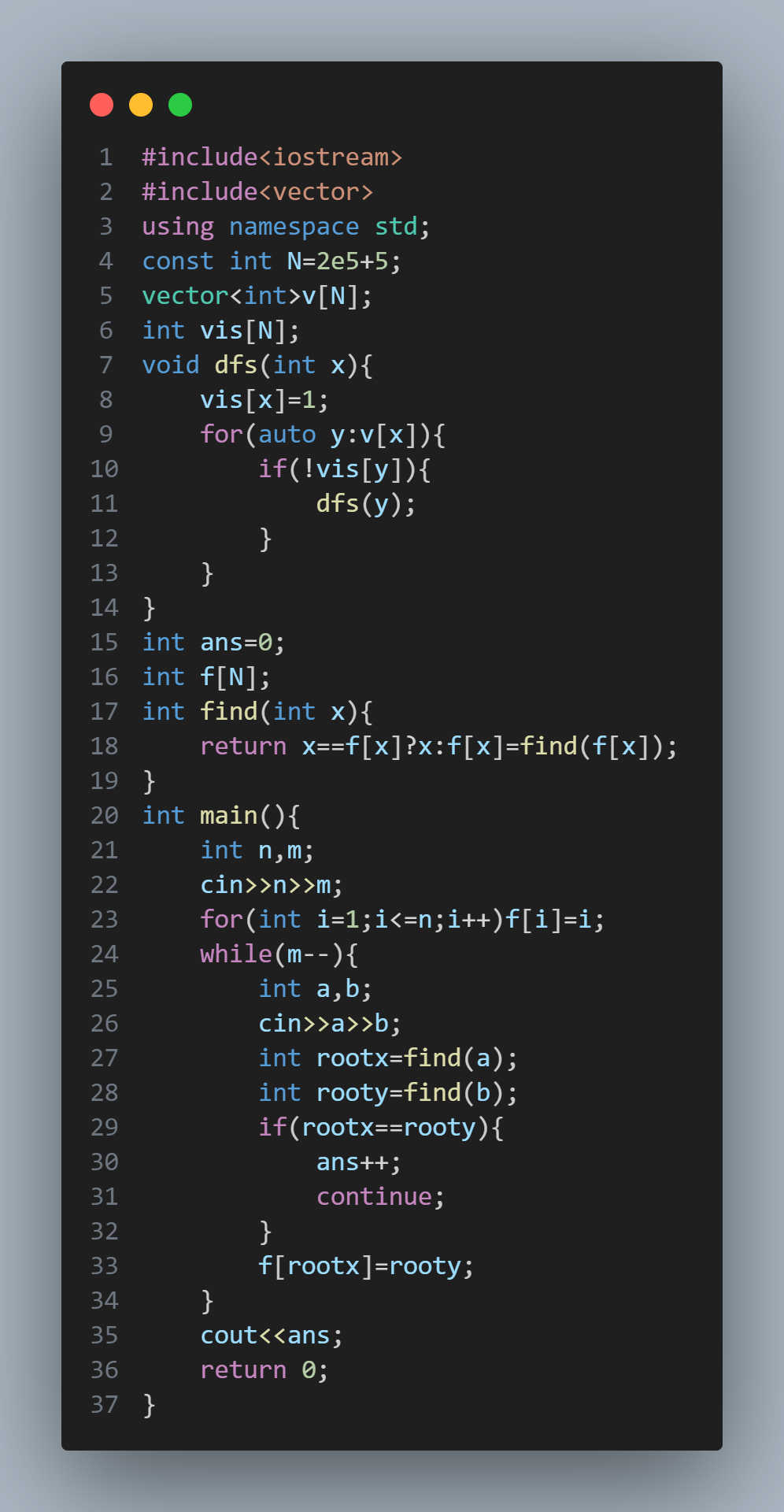
#include<iostream>
#include<vector>
using namespace std;
const int N=2e5+5;
vector<int>v[N];
int vis[N];
void dfs(int x){
    vis[x]=1;
    for(auto y:v[x]){
        if(!vis[y]){
            dfs(y);
        }
    }
}
int ans=0;
int f[N];
int find(int x){
    return x==f[x]?x:f[x]=find(f[x]);
}
int main(){
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)f[i]=i;
    while(m--){
        int a,b;
        cin>>a>>b;
        int rootx=find(a);
        int rooty=find(b);
        if(rootx==rooty){
            ans++;
            continue;
        }
        f[rootx]=rooty;
    }
    cout<<ans;
    return 0;
}