P8435 【模板】点双连通分量

P8435 【模板】点双连通分量

题目描述

对于一个 \(n\) 个节点 \(m\) 条无向边的图，请输出其点双连通分量的个数，并且输出每个点双连通分量。

输入格式

第一行，两个整数 \(n\) 和 \(m\)。

接下来 \(m\) 行，每行两个整数 \(u, v\)，表示一条无向边。

输出格式

第一行一个整数 \(x\) 表示点双连通分量的个数。

接下来的 \(x\) 行，每行第一个数 \(a\) 表示该分量结点个数，然后 \(a\) 个数，描述一个点双连通分量。

你可以以任意顺序输出点双连通分量与点双连通分量内的结点。

输入输出样例 #1

输入 #1

5 8
1 3
2 4
4 3
1 2
4 5
5 1
2 4
1 1

输出 #1

1
5 1 2 3 4 5

输入输出样例 #2

输入 #2

5 3
1 2
2 3
1 3

输出 #2

3
1 4
1 5
3 1 2 3

输入输出样例 #3

输入 #3

6 5
1 3
2 4
1 2
4 6
2 3

输出 #3

4
2 6 4
2 4 2
3 3 2 1
1 5

输入输出样例 #4

输入 #4

7 8
1 3
2 4
3 5
2 5
6 4
2 5
6 3
2 7

输出 #4

3
2 7 2
5 5 2 4 6 3
2 3 1

输入输出样例 #5

输入 #5

1 1
1 1

输出 #5

1
1 1

说明/提示

样例四解释：

相同颜色的点为同一个分量里的结点。

温馨提示：请认真考虑孤立点与自环（样例五）的情况。

---

数据范围：
对于 \(100\%\) 的数据，\(1 \le n \le 5 \times10 ^5\)，\(1 \le m \le 2 \times 10^6\)。

subtask	\(n\)	\(m\)	分值
\(1\)	\(1 \le n \le 100\)	\(1 \le m \le 500\)	\(25\)
\(2\)	\(1 \le n \le 5000\)	\(1 \le m \le 5 \times 10^4\)	\(25\)
\(3\)	\(1 \le n \le 2\times 10^5\)	\(1 \le m \le 5\times 10^5\)	\(25\)
\(4\)	\(1 \le n \le 5 \times10 ^5\)	\(1 \le m \le 2 \times 10^6\)	\(25\)

本题不卡常，时间限制与空间限制均已开大，正确的解法均可通过。

---

数据更新

• \(2022/7/14\) 加强数据
• \(2022/11/26\) 新增 \(10\) 组较小的数据（\(1\le n, m \le 10\))，方便选手调试。
• \(2022/12/31\) 重组 \(subtask\)，并加入若干组极端数据。
• \(2023/1/1\) 发现昨天新加入的数据出了问题，已修改。

---

惊喜：AC 后记得把鼠标放到测试点上看反馈信息，有惊喜哦。
首先点双连通分量最重要的一点就是，一个割点会在多个双连通分量中
首先如果x后面只入了一个点，说明x和y构成一个连通分量，应该把x也加入，
如果low[y]=dfsn[x]那么说明，y只能返回x，也应该把x加入双连通分量中，
如果low[y]>dfsn[x],或者dcc[cnt].szie()大于1说明，x和y单独构成一个双连通分量，
如果x没有子节点，说明x单独作为一个连通分量

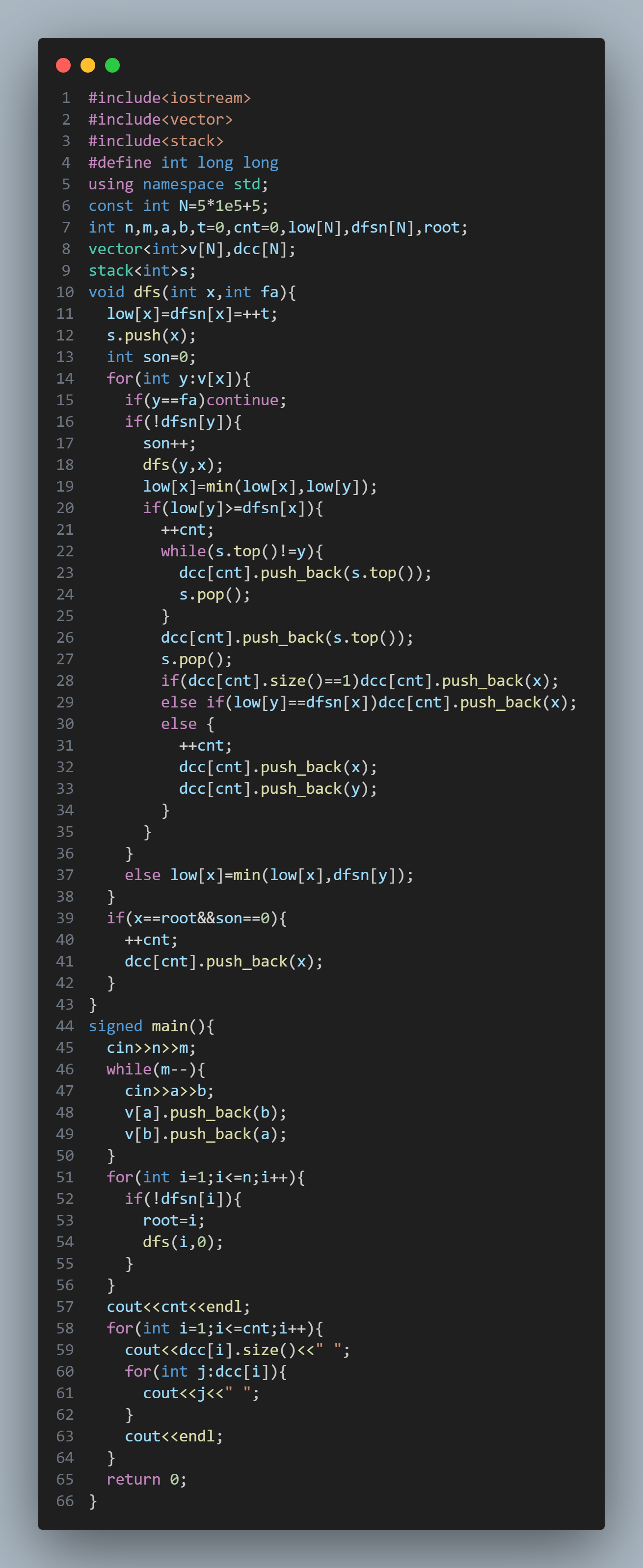
#include<iostream>
#include<vector>
#include<stack>
#define int long long 
using namespace std;
const int N=5*1e5+5;
int n,m,a,b,t=0,cnt=0,low[N],dfsn[N],root;
vector<int>v[N],dcc[N];
stack<int>s;
void dfs(int x,int fa){
  low[x]=dfsn[x]=++t;
  s.push(x);
  int son=0;
  for(int y:v[x]){
    if(y==fa)continue;
    if(!dfsn[y]){
      son++;
      dfs(y,x);
      low[x]=min(low[x],low[y]);
      if(low[y]>=dfsn[x]){
        ++cnt;
        while(s.top()!=y){
          dcc[cnt].push_back(s.top());
          s.pop();
        }
        dcc[cnt].push_back(s.top());
        s.pop();
        if(dcc[cnt].size()==1)dcc[cnt].push_back(x);
        else if(low[y]==dfsn[x])dcc[cnt].push_back(x);
        else {
          ++cnt;
          dcc[cnt].push_back(x);
          dcc[cnt].push_back(y);
        }
      }
    }
    else low[x]=min(low[x],dfsn[y]);
  }
  if(x==root&&son==0){
    ++cnt;
    dcc[cnt].push_back(x);
  }
}
signed main(){
  cin>>n>>m;
  while(m--){
    cin>>a>>b;
    v[a].push_back(b);
    v[b].push_back(a);
  }
  for(int i=1;i<=n;i++){
    if(!dfsn[i]){
      root=i;
      dfs(i,0);
    }
  }
  cout<<cnt<<endl;
  for(int i=1;i<=cnt;i++){
    cout<<dcc[i].size()<<" ";
    for(int j:dcc[i]){
      cout<<j<<" ";
    }
    cout<<endl;
  }
  return 0;
}