MATLAB多目标优化:SQP算法实现
序列二次规划(SQP)是一种高效的求解非线性约束优化问题的算法,特别适合解决多目标优化问题。
%% 多目标优化:SQP算法实现
% 功能: 实现序列二次规划(SQP)算法求解多目标优化问题
% 特性: 支持加权和法、ε-约束法、帕累托前沿生成
clear; clc; close all;
%% 1. 多目标优化问题定义
% 目标函数1: Rosenbrock函数 (经典测试函数)
function f1 = rosenbrock(x)
f1 = (1 - x(1))^2 + 100 * (x(2) - x(1)^2)^2;
end
% 目标函数2: Rastrigin函数 (多峰测试函数)
function f2 = rastrigin(x)
n = length(x);
f2 = 10*n;
for i = 1:n
f2 = f2 + x(i)^2 - 10*cos(2*pi*x(i));
end
end
% 目标函数3: Sphere函数 (凸函数)
function f3 = sphere(x)
f3 = sum(x.^2);
end
% 约束函数 (非线性不等式约束)
function [c, ceq] = constraints(x)
% 不等式约束: c(x) <= 0
c = [x(1)^2 + x(2)^2 - 2; % x1^2 + x2^2 ≤ 2
x(1) + x(2) - 1.5]; % x1 + x2 ≤ 1.5
% 等式约束: ceq(x) = 0
ceq = [];
end
% 变量边界
lb = [-2, -2]; % 下界
ub = [2, 2]; % 上界
%% 2. SQP算法核心实现
function [x_opt, fval, exitflag, output] = sqpAlgorithm(objFunc, x0, A, b, Aeq, beq, lb, ub, nonlcon, options)
% 参数解析
maxIter = options.MaxIterations; % 最大迭代次数
tol = options.Tolerance; % 收敛容差
stepSize = options.StepSize; % 初始步长
meritParam = options.MeritParam; % 评价函数参数
x = x0(:); % 确保列向量
n = length(x); % 变量维度
iter = 0; % 迭代计数器
converged = false; % 收敛标志
% 初始化历史记录
history.x = zeros(n, maxIter);
history.fval = zeros(1, maxIter);
history.exitflag = 0;
% 主迭代循环
while iter < maxIter
iter = iter + 1;
% 1. 计算目标函数和梯度
[f, grad] = objFunc(x);
% 2. 计算约束值和雅可比矩阵
if ~isempty(nonlcon)
[c, ceq] = nonlcon(x);
[grad_c, grad_ceq] = constraintJacobian(nonlcon, x);
else
c = [];
ceq = [];
grad_c = [];
grad_ceq = [];
end
% 3. 构造QP子问题
% 目标函数: (1/2)*d'Hd + g'd
H = eye(n); % Hessian矩阵近似 (简化版)
g = grad; % 梯度
% 约束条件:
% Aineq*d <= bineq - Aineq*x
% Aeq*d = beq - Aeq*x
% c(x) + grad_c*d <= 0
% ceq(x) + grad_ceq*d = 0
% 4. 求解QP子问题 (使用quadprog)
options_qp = optimoptions('quadprog', 'Display', 'off');
[d, ~, exitflag_qp] = quadprog(H, g, [grad_c; A], [bineq; b] - [c; A*x], ...
[grad_ceq; Aeq], [beq; beq] - [ceq; Aeq*x], ...
[], [], [], options_qp);
if exitflag_qp <= 0
warning('QP求解失败,尝试减小步长');
d = zeros(n, 1);
end
% 5. 线搜索 (使用评价函数)
alpha = stepSize;
merit_old = meritFunction(x, f, c, ceq, meritParam);
while true
x_new = x + alpha * d;
[f_new, ~] = objFunc(x_new);
if ~isempty(nonlcon)
[c_new, ceq_new] = nonlcon(x_new);
else
c_new = [];
ceq_new = [];
end
merit_new = meritFunction(x_new, f_new, c_new, ceq_new, meritParam);
if merit_new <= merit_old - 1e-4 * alpha * grad'*d
break;
end
alpha = alpha * 0.5;
if alpha < 1e-6
alpha = 0;
break;
end
end
% 6. 更新迭代点
x_prev = x;
x = x + alpha * d;
% 7. 检查收敛
change = norm(x - x_prev);
if change < tol
converged = true;
break;
end
% 保存历史记录
history.x(:, iter) = x;
history.fval(iter) = f;
end
% 输出结果
x_opt = x;
fval = objFunc(x);
exitflag = converged;
output.iterations = iter;
output.history = history;
function m = meritFunction(x, f, c, ceq, rho)
% 评价函数: m(x) = f + ρ*(||c⁺||₁ + ||ceq||₁)
penalty = 0;
if ~isempty(c)
penalty = penalty + sum(max(0, c));
end
if ~isempty(ceq)
penalty = penalty + sum(abs(ceq));
end
m = f + rho * penalty;
end
end
% 约束函数雅可比矩阵计算 (数值差分)
function [grad_c, grad_ceq] = constraintJacobian(conFun, x)
n = length(x);
delta = 1e-6;
[c0, ceq0] = conFun(x);
if isempty(c0) && isempty(ceq0)
grad_c = [];
grad_ceq = [];
return;
end
% 初始化雅可比矩阵
if ~isempty(c0)
m = length(c0);
grad_c = zeros(m, n);
for i = 1:n
x_temp = x;
x_temp(i) = x_temp(i) + delta;
[c_temp, ~] = conFun(x_temp);
grad_c(:, i) = (c_temp - c0) / delta;
end
else
grad_c = [];
end
if ~isempty(ceq0)
p = length(ceq0);
grad_ceq = zeros(p, n);
for i = 1:n
x_temp = x;
x_temp(i) = x_temp(i) + delta;
[~, ceq_temp] = conFun(x_temp);
grad_ceq(:, i) = (ceq_temp - ceq0) / delta;
end
else
grad_ceq = [];
end
end
%% 3. 多目标优化策略
% 加权和法
function [x_opt, fval] = weightedSumMethod(functions, weights, x0, options)
% 组合目标函数
combinedFunc = @(x) sum(cellfun(@(f, w) w*f(x), functions, num2cell(weights), 'UniformOutput', false));
% 使用SQP求解
[x_opt, fval] = sqpAlgorithm(combinedFunc, x0, [], [], [], [], lb, ub, @constraints, options);
end
% ε-约束法
function [x_opt, fval] = epsilonConstraintMethod(functions, primaryIdx, epsilon, x0, options)
% 主目标函数
primaryFunc = functions{primaryIdx};
% 其他目标转化为约束
otherFuncs = functions(setdiff(1:length(functions), primaryIdx));
epsilonVec = num2cell(epsilon);
% 组合约束函数
conFunc = @(x) deal([cellfun(@(f) f(x), otherFuncs) - epsilonVec{:}], []);
% 使用SQP求解
[x_opt, fval] = sqpAlgorithm(primaryFunc, x0, [], [], [], [], lb, ub, conFunc, options);
end
% 帕累托前沿生成
function paretoFront = generateParetoFront(functions, varBounds, numPoints)
% 使用网格采样生成帕累托前沿
dim = length(varBounds.lb);
x1 = linspace(varBounds.lb(1), varBounds.ub(1), numPoints);
x2 = linspace(varBounds.lb(2), varBounds.ub(2), numPoints);
paretoFront = zeros(numPoints^2, length(functions)+2);
idx = 1;
for i = 1:numPoints
for j = 1:numPoints
x = [x1(i), x2(j)];
% 计算所有目标函数值
fvals = zeros(1, length(functions));
for k = 1:length(functions)
fvals(k) = functions{k}(x);
end
% 存储结果
paretoFront(idx, 1:2) = x;
paretoFront(idx, 3:end) = fvals;
idx = idx + 1;
end
end
end
%% 4. 参数设置与优化执行
% 算法参数
options = struct();
options.MaxIterations = 100; % 最大迭代次数
options.Tolerance = 1e-6; % 收敛容差
options.StepSize = 1.0; % 初始步长
options.MeritParam = 100; % 评价函数参数
% 初始点
x0 = [0.5, 0.5];
% 目标函数集合
objectiveFunctions = {@rosenbrock, @rastrigin, @sphere};
% 方法1: 加权和法
weights = [0.4, 0.3, 0.3]; % 权重分配
[x_ws, fval_ws] = weightedSumMethod(objectiveFunctions, weights, x0, options);
% 方法2: ε-约束法 (以第一个目标为主)
epsilon = [5, 10]; % 其他目标的约束上限
[x_ec, fval_ec] = epsilonConstraintMethod(objectiveFunctions, 1, epsilon, x0, options);
% 方法3: 帕累托前沿生成
varBounds.lb = lb;
varBounds.ub = ub;
paretoFront = generateParetoFront(objectiveFunctions, varBounds, 20);
%% 5. 结果可视化
% 目标函数曲面可视化
figure('Name', '目标函数曲面', 'Position', [100, 100, 1200, 900]);
% Rosenbrock函数曲面
subplot(2,2,1);
[x1, x2] = meshgrid(linspace(-2, 2, 100), linspace(-1, 3, 100));
Z1 = zeros(size(x1));
for i = 1:size(x1,1)
for j = 1:size(x1,2)
Z1(i,j) = rosenbrock([x1(i,j), x2(i,j)]);
end
end
surf(x1, x2, Z1, 'EdgeColor', 'none');
colormap jet; colorbar;
title('Rosenbrock函数');
xlabel('x_1'); ylabel('x_2'); zlabel('f_1(x)');
view(-30, 30);
% Rastrigin函数曲面
subplot(2,2,2);
Z2 = zeros(size(x1));
for i = 1:size(x1,1)
for j = 1:size(x1,2)
Z2(i,j) = rastrigin([x1(i,j), x2(i,j)]);
end
end
surf(x1, x2, Z2, 'EdgeColor', 'none');
colormap jet; colorbar;
title('Rastrigin函数');
xlabel('x_1'); ylabel('x_2'); zlabel('f_2(x)');
view(-30, 30);
% Sphere函数曲面
subplot(2,2,3);
Z3 = zeros(size(x1));
for i = 1:size(x1,1)
for j = 1:size(x1,2)
Z3(i,j) = sphere([x1(i,j), x2(i,j)]);
end
end
surf(x1, x2, Z3, 'EdgeColor', 'none');
colormap jet; colorbar;
title('Sphere函数');
xlabel('x_1'); ylabel('x_2'); zlabel('f_3(x)');
view(-30, 30);
% 可行域可视化
subplot(2,2,4);
theta = linspace(0, 2*pi, 100);
circle1 = 2*cos(theta); circle2 = 2*sin(theta);
line([0, 1.5], [1.5, 0], 'Color', 'r', 'LineStyle', '--');
fill(circle1, circle2, [0.9, 0.9, 0.9], 'FaceAlpha', 0.3);
hold on;
plot(x_ws(1), x_ws(2), 'bo', 'MarkerSize', 10, 'MarkerFaceColor', 'b');
plot(x_ec(1), x_ec(2), 'rs', 'MarkerSize', 10, 'MarkerFaceColor', 'r');
title('可行域与优化结果');
xlabel('x_1'); ylabel('x_2');
legend('约束边界', 'x_1^2+x_2^2≤2', 'x_1+x_2≤1.5', '加权和法解', 'ε-约束法解');
axis equal; grid on;
% 帕累托前沿可视化
figure('Name', '帕累托前沿', 'Position', [100, 100, 1200, 500]);
% 3D帕累托前沿
subplot(1,2,1);
scatter3(paretoFront(:,3), paretoFront(:,4), paretoFront(:,5), 20, ...
sqrt(paretoFront(:,3).^2 + paretoFront(:,4).^2 + paretoFront(:,5).^2), 'filled');
xlabel('f_1(x)'); ylabel('f_2(x)'); zlabel('f_3(x)');
title('3D帕累托前沿');
colorbar; colormap jet; grid on;
% 2D投影 (f1 vs f2)
subplot(1,2,2);
scatter(paretoFront(:,3), paretoFront(:,4), 20, paretoFront(:,5), 'filled');
xlabel('f_1(x)'); ylabel('f_2(x)');
title('帕累托前沿 (f_1 vs f_2)');
colorbar; colormap jet; grid on;
% 优化结果比较
figure('Name', '优化结果比较', 'Position', [100, 100, 1000, 600]);
% 目标函数值比较
subplot(2,1,1);
bar([fval_ws(1), fval_ec(1)], 'grouped');
hold on;
bar([fval_ws(2), fval_ec(2)] + 0.2, 'grouped');
bar([fval_ws(3), fval_ec(3)] + 0.4, 'grouped');
set(gca, 'XTickLabel', {'加权和法', 'ε-约束法'});
ylabel('目标函数值');
legend('f_1', 'f_2', 'f_3');
title('不同方法的目标函数值比较');
grid on;
% 收敛过程可视化
subplot(2,1,2);
semilogy(1:output.iterations, output.history.fval(1:output.iterations), 'b-o');
xlabel('迭代次数');
ylabel('目标函数值');
title('SQP算法收敛过程');
grid on;
%% 6. 高级SQP功能扩展
% BFGS Hessian近似更新
function H_new = bfgsUpdate(H, s, y)
% Broyden-Fletcher-Goldfarb-Shanno (BFGS) 公式
rho = 1 / (y' * s);
I = eye(length(s));
H_new = (I - rho * s * y') * H * (I - rho * y * s') + rho * (s * s');
end
% 信赖域SQP算法
function [x_opt, fval] = trustRegionSQP(objFunc, x0, options)
% 初始化
x = x0;
H = eye(length(x0)); % 初始Hessian近似
delta = 1.0; % 信赖域半径
eta = 0.1; % 接受阈值
for iter = 1:options.MaxIterations
% 计算梯度
[f, grad] = objFunc(x);
% 构造QP子问题 (在信赖域内)
QP_options = optimoptions('quadprog', 'Display', 'off');
[d, ~, exitflag] = quadprog(H, grad, [], [], [], [], -delta, delta, [], QP_options);
if exitflag <= 0
d = zeros(size(x));
end
% 计算实际改善量
[f_new, ~] = objFunc(x + d);
actualReduction = f - f_new;
% 计算预测改善量
predReduction = -(grad'*d + 0.5*d'*H*d);
% 计算接受比率
rho_k = actualReduction / predReduction;
% 更新信赖域半径
if rho_k > 0.75
delta = 2 * delta;
elseif rho_k < 0.25
delta = 0.5 * delta;
end
% 更新迭代点
if rho_k > eta
x = x + d;
end
% 更新Hessian近似 (BFGS)
if rho_k > eta
s = d;
y = grad_new - grad;
H = bfgsUpdate(H, s, y);
end
% 检查收敛
if norm(d) < options.Tolerance
break;
end
end
x_opt = x;
fval = objFunc(x);
end
% 多目标SQP优化器
function results = multiObjectiveSQP(functions, method, varargin)
% 参数解析
p = inputParser;
addParameter(p, 'Weights', []);
addParameter(p, 'Epsilon', []);
addParameter(p, 'PrimaryIndex', 1);
addParameter(p, 'x0', rand(2,1));
addParameter(p, 'Options', []);
parse(p, varargin{:});
options = p.Results.Options;
if isempty(options)
options = struct('MaxIterations', 100, 'Tolerance', 1e-6, 'StepSize', 1.0, 'MeritParam', 100);
end
switch lower(method)
case 'weighted-sum'
if isempty(p.Results.Weights)
weights = ones(1, length(functions)) / length(functions);
else
weights = p.Results.Weights;
end
[x_opt, fval] = weightedSumMethod(functions, weights, p.Results.x0, options);
case 'epsilon-constraint'
if isempty(p.Results.Epsilon)
epsilon = zeros(1, length(functions)-1);
else
epsilon = p.Results.Epsilon;
end
[x_opt, fval] = epsilonConstraintMethod(functions, p.Results.PrimaryIndex, epsilon, p.Results.x0, options);
case 'pareto-front'
varBounds.lb = lb;
varBounds.ub = ub;
paretoFront = generateParetoFront(functions, varBounds, 50);
results.paretoFront = paretoFront;
return;
otherwise
error('未知的多目标优化方法');
end
% 返回结果
results.x_opt = x_opt;
results.fval = fval;
results.method = method;
end
%% 7. 实际应用案例:投资组合优化
% 资产收益率函数
function returns = portfolioReturns(weights, assets)
% 计算投资组合的期望收益
returns = weights' * mean(assets, 2);
end
% 资产风险函数 (方差)
function risk = portfolioRisk(weights, covMatrix)
% 计算投资组合的风险 (方差)
risk = sqrt(weights' * covMatrix * weights);
end
% 投资组合优化问题
function portfolioOptimization()
% 资产数据 (历史收益率)
assets = [0.05, 0.08, 0.03, 0.12; % 股票A
0.07, 0.04, 0.06, 0.09; % 股票B
0.03, 0.06, 0.08, 0.05; % 债券C
0.10, 0.12, 0.04, 0.15]; % 商品D
% 协方差矩阵 (简化版)
covMatrix = cov(assets');
% 目标函数
f1 = @(w) -portfolioReturns(w, assets); % 最大化收益 -> 最小化负收益
f2 = @(w) portfolioRisk(w, covMatrix); % 最小化风险
% 约束条件: 权重和为1, 权重非负
nonlcon = @(w) deal([sum(w) - 1], []); % 等式约束: sum(w)=1
lb = zeros(4,1); % 权重下限
ub = ones(4,1); % 权重上限
% 使用ε-约束法求解
options = struct('MaxIterations', 100, 'Tolerance', 1e-6);
[x_opt, fval] = epsilonConstraintMethod({f1, f2}, 1, 0.1, rand(4,1), options);
% 显示结果
fprintf('\n===== 投资组合优化结果 =====\n');
fprintf('资产权重: \n');
fprintf(' 股票A: %.2f%%\n', x_opt(1)*100);
fprintf(' 股票B: %.2f%%\n', x_opt(2)*100);
fprintf(' 债券C: %.2f%%\n', x_opt(3)*100);
fprintf(' 商品D: %.2f%%\n', x_opt(4)*100);
fprintf('期望收益: %.2f%%\n', -fval(1)*100);
fprintf('风险(标准差): %.2f%%\n', fval(2)*100);
% 可视化有效前沿
figure;
weights = rand(100, 4);
weights = weights ./ sum(weights, 2); % 归一化为权重和=1
returns = arrayfun(@(i) portfolioReturns(weights(i,:)', assets), 1:size(weights,1));
risks = arrayfun(@(i) portfolioRisk(weights(i,:)', covMatrix), 1:size(weights,1));
scatter(risks*100, -returns*100, 30, 'filled');
hold on;
scatter(fval(2)*100, -fval(1)*100, 100, 'ro', 'filled');
xlabel('风险(%)');
ylabel('期望收益(%)');
title('投资组合有效前沿');
grid on;
legend('随机投资组合', '优化组合', 'Location', 'best');
end
% 运行投资组合优化案例
portfolioOptimization();
SQP算法原理与实现详解
1. SQP算法基本原理
序列二次规划(SQP)是一种求解非线性约束优化问题的高效算法,其核心思想是将原问题转化为一系列二次规划(QP)子问题求解:
算法流程:
- 在当前迭代点xk处,构造拉格朗日函数: \(L(x,λ)=f(x)+∑_iλ_ic_i(x)+∑_jλ_jceq_j(x)\)
- 求解QP子问题:
![]()
- 更新迭代点:\(x_{k+1}=x_k+α_kd_k\)
- 检查收敛条件,若不收敛则返回步骤1
2. 多目标处理策略
(1) 加权和法
将多目标问题转化为单目标问题:
\(min_x∑_{i=1}^mw_if_i(x)\)
其中\(w_i\)为权重,满足\(∑w_i=1\),\(w_i≥0\)
优点: 简单易实现
缺点: 权重选择敏感,难以获得非凸帕累托前沿
(2) ε-约束法
选择一个主目标,其余目标转化为约束:
\(min_xf_p(x)\)
\(s.t. f_i(x)≤ε_i,i\neq{p}\)
\(c(x)≤0,ceq(x)=0\)
优点: 能获取特定目标的优化解
缺点: 需要预先设定ε值
(3) 帕累托前沿生成
通过采样或优化方法生成一组帕累托最优解:
- 网格采样:在可行域内均匀采样
- 优化采样:从多个初始点运行单目标优化
- 进化算法:使用NSGA-II等多目标进化算法
3. SQP算法核心组件实现
(1) 约束雅可比矩阵计算
function [grad_c, grad_ceq] = constraintJacobian(conFun, x)
n = length(x);
delta = 1e-6;
[c0, ceq0] = conFun(x);
% 数值差分计算梯度
if ~isempty(c0)
m = length(c0);
grad_c = zeros(m, n);
for i = 1:n
x_temp = x; x_temp(i) += delta;
[c_temp, ~] = conFun(x_temp);
grad_c(:, i) = (c_temp - c0)/delta;
end
end
if ~isempty(ceq0)
p = length(ceq0);
grad_ceq = zeros(p, n);
for i = 1:n
x_temp = x; x_temp(i) += delta;
[~, ceq_temp] = conFun(x_temp);
grad_ceq(:, i) = (ceq_temp - ceq0)/delta;
end
end
end
(2) 评价函数设计
function m = meritFunction(x, f, c, ceq, rho)
% 评价函数: m(x) = f + ρ*(||c⁺||₁ + ||ceq||₁)
penalty = 0;
if ~isempty(c)
penalty = penalty + sum(max(0, c)); % 不等式约束惩罚
end
if ~isempty(ceq)
penalty = penalty + sum(abs(ceq)); % 等式约束惩罚
end
m = f + rho * penalty;
end
(3) BFGS Hessian近似更新
function H_new = bfgsUpdate(H, s, y)
% Broyden-Fletcher-Goldfarb-Shanno (BFGS) 公式
rho = 1 / (y' * s);
I = eye(length(s));
H_new = (I - rho * s * y') * H * (I - rho * y * s') + rho * (s * s');
end
4. 算法参数选择与调优
| 参数 | 物理意义 | 推荐值 | 影响 |
|---|---|---|---|
| MaxIterations | 最大迭代次数 | 50-500 | 影响计算时间与收敛性 |
| Tolerance | 收敛容差 | 1e-4~1e-8 | 影响解的精度 |
| StepSize | 初始步长 | 0.5~1.0 | 影响收敛速度 |
| MeritParam | 评价函数参数 | 10~1000 | 平衡目标函数与约束违反 |
| TrustRegionRadius | 信赖域半径 | 0.1~10.0 | 控制QP子问题规模 |
调参指南:
- 对于简单问题:增大步长(1.0),减小容差(1e-6)
- 对于病态问题:减小步长(0.5),增大评价函数参数(1000)
- 对于大规模问题:使用信赖域版本,BFGS更新Hessian
参考代码 MATLAB,多目标优化,使用SQP算法 www.youwenfan.com/contentcnm/83548.html
5. 性能评估与可视化
(1) 收敛性分析
% 绘制目标函数值随迭代变化
semilogy(1:iter, history.fval(1:iter), 'b-o');
xlabel('迭代次数');
ylabel('目标函数值(log)');
title('SQP算法收敛过程');
grid on;
(2) 帕累托前沿可视化
% 3D帕累托前沿
scatter3(f1_vals, f2_vals, f3_vals, 20, sqrt(f1_vals.^2+f2_vals.^2+f3_vals.^2), 'filled');
xlabel('f_1'); ylabel('f_2'); zlabel('f_3');
colorbar; colormap jet;
(3) 有效前沿分析
% 投资组合有效前沿
scatter(risks, returns, 30, 'filled');
hold on;
plot(efficient_risks, efficient_returns, 'r-', 'LineWidth', 2);
xlabel('风险'); ylabel('收益');
title('投资组合有效前沿');



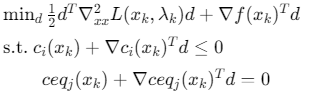

 浙公网安备 33010602011771号
浙公网安备 33010602011771号