基于MATLAB的LBFGS优化算法实现

一、LBFGS算法原理与数学模型

LBFGS（Limited-memory Broyden-Fletcher-Goldfarb-Shanno）是一种改进的拟牛顿法，通过存储最近m步的梯度差和变量差来近似Hessian矩阵逆，显著降低内存需求。其核心步骤包括：

1. 搜索方向计算：利用双循环递归算法生成下降方向 \(pk=−Bkgk\)
2. 线搜索确定步长：采用强Wolfe条件确定最优步长 \(αk\)
3. 变量更新：
4. Hessian近似更新：通过递推公式更新 Bk+1

数学表达式：

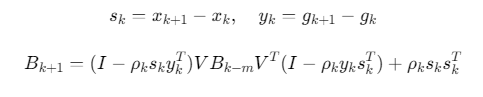
其中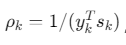，V为投影矩阵

---

二、MATLAB实现步骤

1. 基础实现（使用内置函数）

% 定义目标函数及梯度
fun = @(x) (x(1)-1).^2 + (x(2)-2).^4;  % 示例目标函数
grad = @(x) [2*(x(1)-1); 4*(x(2)-2).^3];

% 设置优化选项
options = optimoptions('fminunc',...
    'Algorithm', 'quasi-newton',...
    'GradObj', 'on',...
    'Display', 'iter',...
    'MaxIter', 1000,...
    'TolFun', 1e-6);

% 初始猜测
x0 = [0; 0];

% 执行优化
[x_opt, fval, exitflag] = fminunc(fun, x0, options);

2. 自定义LBFGS实现（双循环递归）

function [x, f, g, out] = myLBFGS(fun, grad, x0, m, maxit, tol)
    % 初始化
    x = x0;
    [f, g] = fun(x);
    n = length(x);
    S = zeros(n,m); Y = zeros(n,m);
    rho = zeros(m,1);
    k = 0;
    
    % 主循环
    while norm(g) > tol && k < maxit
        % 计算搜索方向
        p = -getDirection(g, S, Y, rho);
        
        % 线搜索
        alpha = backtrackingLineSearch(fun, grad, x, p, g);
        
        % 更新变量
        x_new = x + alpha*p;
        [f_new, g_new] = fun(x_new);
        
        % 更新历史信息
        s = x_new - x;
        y = g_new - g;
        rho(end+1) = 1/(y'*s);
        S(:,end) = s;
        Y(:,end) = y;
        
        % 维护历史窗口
        if size(S,2) > m
            S(:,1) = [];
            Y(:,1) = [];
            rho(1) = [];
        end
        
        x = x_new;
        f = f_new;
        g = g_new;
        k = k+1;
    end
    out.iter = k;
end

function p = getDirection(g, S, Y, rho)
    q = g;
    alpha = zeros(size(rho));
    for i = length(rho):-1:1
        alpha(i) = rho(i) * S(:,i)'*q;
        q = q - alpha(i)*Y(:,i);
    end
    r = (S(:,end)'*Y(:,end))/(Y(:,end)'*S(:,end)) * q;
    for i = 1:length(rho)
        beta = rho(i) * Y(:,i)'*r;
        r = r + S(:,i)*(alpha(i) - beta);
    end
    p = -r;
end

参考代码 基于matlab的LBFGS优化算法 www.youwenfan.com/contentcni/64465.html

三、参数调优

参数	推荐范围	作用说明
m(内存步数)	5-20	平衡计算效率与近似精度
TolFun	1e-6~1e-8	函数值收敛阈值
MaxIter	1000-10000	防止无限循环
LineSearch	Wolfe条件	确保充分下降和曲率条件

优化示例：

% 自适应内存步长选择
m = min(20, floor(0.1*size(x0,2))); 

% 高精度收敛设置
options = optimoptions('fminunc',...
    'Algorithm', 'lbfgs',...
    'SpecifyObjectiveGradient', true,...
    'HessianApproximation', 'lbfgs',...
    'OptimalityTolerance', 1e-8);

---

四、性能优化

1. 预处理加速：

   % 变量缩放
   x_scaled = (x - mean(x))/std(x);
   

2. 并行计算：

   % 使用parfor加速梯度计算
   parfor i = 1:n
       grad(i) = compute_gradient(x(i));
   end
   

3. GPU加速：

   x_gpu = gpuArray(x);
   [x_opt, fval] = fminunc(@(x) gpuObjFun(x), x_gpu);
   

---

五、应用案例：图像去模糊

1. 问题建模

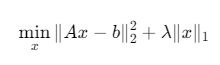
其中A为模糊算子，b为观测图像

2. MATLAB实现

% 加载模糊图像
load('blurred_image.mat');
b = double(blurred_img);
[m,n] = size(b);

% 定义目标函数
fun = @(x) 0.5*norm(A*x - b)^2 + lambda*norm(x,1);
grad = @(x) A'*(A*x - b) + lambda*sign(x);

% 初始猜测
x0 = zeros(m,n);

% 执行LBFGS优化
options = optimoptions('fminunc',...
    'Algorithm', 'lbfgs',...
    'GradObj', 'on',...
    'MaxIter', 500);
[x_recon, fval] = fminunc(fun, x0, options);

% 显示结果
figure;
subplot(1,2,1); imshow(uint8(b)); title('模糊图像');
subplot(1,2,2); imshow(uint8(x_recon)); title('重建图像');