【题解】P3727 曼哈顿计划E简要推理过程

题目

当字体为紫色时，代表题目的具体实现做法。

总结：Nim游戏的小trick：将元素的值设为最大可操作次数就能用普通 Nim 了！。

\(k=1\)

直接 \(\text{nim}\) 游戏。异或和为 0 时则获胜。

\(k=2\)

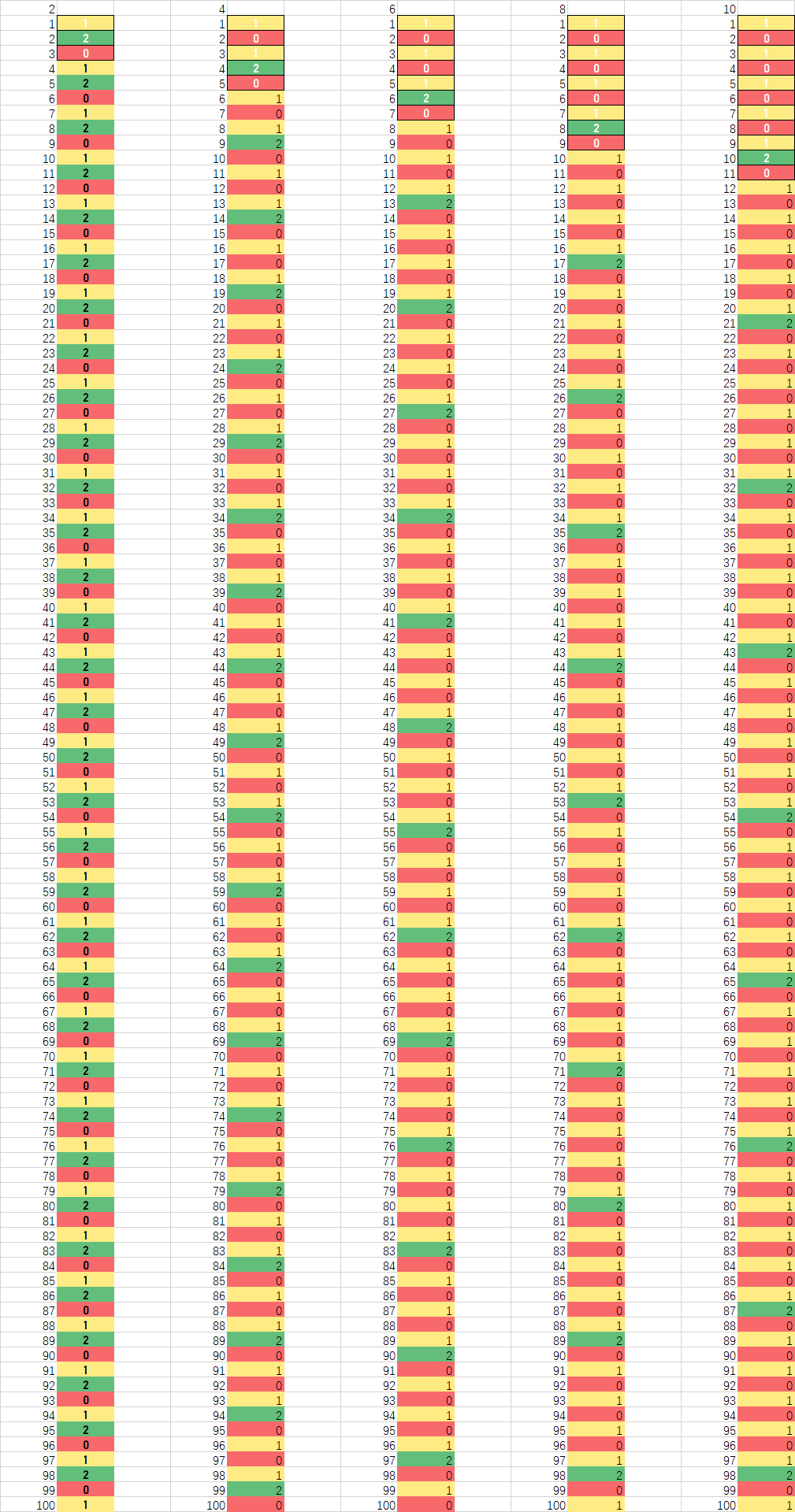
\(k=3\)

对于每一个数 \(x\)，最多肯定会被减少 \(\left\lfloor\displaystyle\frac{x}{s} \right\rfloor\) 次。每多挪动一点相当于多取了一次，不可能一次都不动，也是一个 \(\text{nim}\) 游戏。

所以可以将 \(x\) 改为 \(\left\lfloor\displaystyle\frac{x}{s} \right\rfloor\)，然后异或起来为 \(0\) 时取胜。

\(k=4\)

Code

#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
//#define int long long
namespace gtx{
//	Fast IO
	void read(int &x){
		x = 0;int h = 1;char tmp;
		do{tmp=getchar();if(tmp=='-')h*=-1;}while(!isdigit(tmp));
		while(isdigit(tmp)) x*=10,x+=tmp-'0',tmp=getchar();
		x*=h;
	}
	void read(char &x){do{x=getchar();}while(x==' '||x=='\n'||x=='\r');}
	void write(char x){putchar(x);}
	void write(int x){
		if(x<0) putchar('-'),x=-x;int st[200]={0},tot=0;
		do st[++tot]=x%10,x/=10; while(x);
		while(tot){putchar(st[tot--]+'0');}
	}
	void write(int x,char y){write(x);write(y);}
#ifndef int
	void read(long long &x){
		x = 0;int h = 1;char tmp;
		do{tmp=getchar();if(tmp=='-')h*=-1;}while(!isdigit(tmp));
		while(isdigit(tmp)) x*=10,x+=tmp-'0',tmp=getchar();
		x*=h;
	}
	void write(long long x){
		if(x<0) putchar('-'),x=-x;int st[200]={0},tot=0;
		do st[++tot]=x%10,x/=10; while(x);
		while(tot){putchar(st[tot--]+'0');}
	}
	void write(long long x,char y){write(x);write(y);}
#endif
	const int MAXN = 3e4+10;
	vector<int> v[MAXN];
	int n,a[MAXN];
	namespace k1{
		bool can_be_0;
		int delta[MAXN];
		set<int> dfs(int k,int fath){
			set<int> st,st2,*now,*t;
			now = &st;t = &st2;
//			st.insert(0);
			st.insert(a[k]);
			delta[k] = 0;
			if(a[k]==0) can_be_0 = 1;
			for(int i:v[k]){
				if(i==fath) continue;
				*t = dfs(i,k);
				if(t->size()<now->size()){
					for(int j:*t){
						if(now->find(j^delta[i]^delta[k])!=now->end()) can_be_0 = 1;
					}
					for(int j:*t){
						now->insert(j^delta[i]^delta[k]^a[k]);
					}
				}else{
					for(int j:*now){
						if(t->find(j^delta[k]^delta[i])!=t->end()) can_be_0 = 1;
					}
					int recentdel = delta[k];
					delta[k] = delta[i]^a[k];
					for(int j:*now){
						t->insert(j^recentdel^delta[k]);
					}
					swap(t,now);
				}
			}
			return *now;
		}
	}
	namespace k3{
		bool can_be_0;
		int delta[MAXN];
		set<int> dfs(int k,int fath){
			set<int> st,st2,*now,*t;
			now = &st;t = &st2;
//			st.insert(0);
			st.insert(a[k]);
			delta[k] = 0;
			if(a[k]==0) can_be_0 = 1;
			for(int i:v[k]){
				if(i==fath) continue;
				*t = dfs(i,k);
				if(t->size()<now->size()){
					for(int j:*t){
						if(now->find(j^delta[i]^delta[k])!=now->end()) can_be_0 = 1;
					}
					for(int j:*t){
						now->insert(j^delta[i]^delta[k]^a[k]);
					}
				}else{
					for(int j:*now){
						if(t->find(j^delta[k]^delta[i])!=t->end()) can_be_0 = 1;
					}
					int recentdel = delta[k];
					delta[k] = delta[i]^a[k];
					for(int j:*now){
						t->insert(j^recentdel^delta[k]);
					}
					swap(t,now);
				}
			}
			return *now;
		}
	}
	namespace k4{
		bool can_be_0;
		int delta[MAXN];
		set<int> dfs(int k,int fath){
			set<int> st,st2,*now,*t;
			now = &st;t = &st2;
//			st.insert(0);
			st.insert(a[k]);
			delta[k] = 0;
			if(a[k]==0) can_be_0 = 1;
			for(int i:v[k]){
				if(i==fath) continue;
				*t = dfs(i,k);
				if(t->size()<now->size()){
					for(int j:*t){
						if(now->find(j^delta[i]^delta[k])!=now->end()) can_be_0 = 1;
					}
					for(int j:*t){
						now->insert(j^delta[i]^delta[k]^a[k]);
					}
				}else{
					for(int j:*now){
						if(t->find(j^delta[k]^delta[i])!=t->end()) can_be_0 = 1;
					}
					int recentdel = delta[k];
					delta[k] = delta[i]^a[k];
					for(int j:*now){
						t->insert(j^recentdel^delta[k]);
					}
					swap(t,now);
				}
			}
			return *now;
		}
	}
	namespace k2{
		bool can_be_0;
		int delta[MAXN];
		set<int> dfs(int k,int fath){
			set<int> st,st2,*now,*t;
			now = &st;t = &st2;
//			st.insert(0);
			st.insert(a[k]);
			delta[k] = 0;
			if(a[k]==0) can_be_0 = 1;
			for(int i:v[k]){
				if(i==fath) continue;
				*t = dfs(i,k);
				if(t->size()<now->size()){
					for(int j:*t){
						if(now->find(j^delta[i]^delta[k])!=now->end()) can_be_0 = 1;
					}
					for(int j:*t){
						now->insert(j^delta[i]^delta[k]^a[k]);
					}
				}else{
					for(int j:*now){
						if(t->find(j^delta[k]^delta[i])!=t->end()) can_be_0 = 1;
					}
					int recentdel = delta[k];
					delta[k] = delta[i]^a[k];
					for(int j:*now){
						t->insert(j^recentdel^delta[k]);
					}
					swap(t,now);
				}
			}
			return *now;
		}
	}
	signed main(){
		read(n);
		for(int i = 1;i<=n;i++) v[i].clear();
		for(int i = 1;i<n;i++){
			int x,y;
			read(x);read(y);
			v[x].push_back(y);
			v[y].push_back(x);
		}
		for(int i = 1;i<=n;i++){
			read(a[i]);
		}
		int k;read(k);
		if(k==1){
			k1::can_be_0 = 0;
			k1::dfs(1,0);
			if(k1::can_be_0) puts("Mutalisk ride face how to lose?");
			else puts("The commentary cannot go on!");
		}else if(k==3){
			int s;read(s);
			for(int i = 1;i<=n;i++){
				a[i] = a[i]/s;
			}
			k3::can_be_0 = 0;
			k3::dfs(1,0);
			if(k3::can_be_0) puts("Mutalisk ride face how to lose?");
			else puts("The commentary cannot go on!");
		}else if(k==4){
			for(int i = 1;i<=n;i++){
				if(a[i]%4==1){
					a[i]=a[i];
				}else if(a[i]%4==2){
					a[i]=a[i];
				}else if(a[i]%4==3){
					a[i]++;
				}else{
					a[i]--;
				}
			}
			k4::can_be_0 = 0;
			k4::dfs(1,0);
			if(k4::can_be_0) puts("Mutalisk ride face how to lose?");
			else puts("The commentary cannot go on!");
			
		}else{
			int s;
			read(s);
			if(s&1){
				for(int i = 1;i<=n;i++){
					a[i] = a[i]&1;
				}
			}else{
				for(int i = 1;i<=n;i++){
					if(a[i]%(s+1)<s){
						a[i] = (a[i]%(s+1))&1;
					}else if(a[i]%(s+1)){
						a[i] = 2;
					}else{
						a[i] = 0;
					}
				}
			}
			k2::can_be_0 = 0;
			k2::dfs(1,0);
			if(k2::can_be_0) puts("Mutalisk ride face how to lose?");
			else puts("The commentary cannot go on!");
			
			
		}
		return 0;
	}
}
signed main(){
//	freopen("P3727_1.in","r",stdin);
//	freopen(".out","w",stdout);
//	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	int T = 1;
	gtx::read(T);
	while(T--) gtx::main();
	return 0;
}