[JSOI2015] 染色问题

[JSOI2015] 染色问题

题目描述

萌萌家有一个棋盘，这个棋盘是一个 \(n \times m\) 的矩形，分成 \(n\) 行 \(m\) 列共 \(n \times m\) 个小方格。
现在萌萌和南南有 \(C\) 种不同颜色的颜料，他们希望把棋盘用这些颜料染色，并满足以下规定：

1. 棋盘的每一个小方格既可以染色（染成 \(C\) 种颜色中的一种），也可以不染色。
2. 棋盘的每一行至少有一个小方格被染色。
3. 棋盘的每一列至少有一个小方格被染色。
4. 每种颜色都在棋盘上出现至少一次。

以下是一些将 \(3 \times 3\) 棋盘染成 \(C=3\) 种颜色（红、黄、蓝）的例子（下图已更新）：

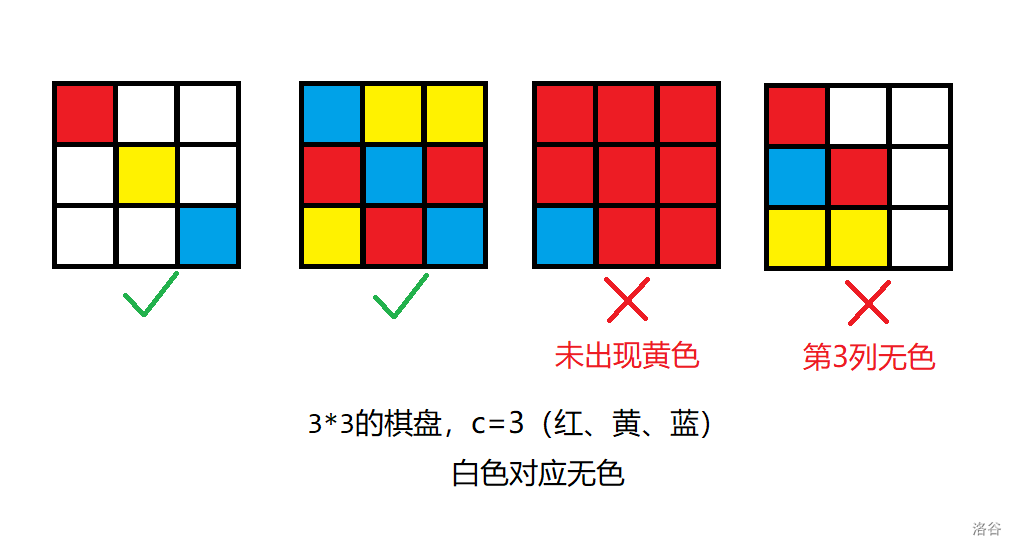
请你求出满足要求的不同的染色方案总数。只要存在一个位置的颜色不同，即认为两个染色方案是不同的。

输入格式

输入只有一行，为 \(3\) 个整数 \(n,m,c\)。

输出格式

输出一个整数，为不同染色方案总数。
因为总数可能很大，只需输出总数对 \(1,000,000,007\) 取模的值。

样例 #1

样例输入 #1

2 2 3

样例输出 #1

60

提示

对于\(100\%\)的数据，\(1 \le n,m,c \le 400\)。

思路分析

\(O(nmc\log c)\)，\(400\times 400\times 400\times 9=576\,000\,000\)，（在网上找一些离奇的卡场方法就能过）

代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN = 410;
const int MOD = 1e9+7;
int n,m,c,ans;
long long mm, p;
void init(int pp) { mm = ((__int128)1 << 64) / pp; p = pp; }
inline long long o(const long long x)
{
    return x - ((__int128(x) * mm) >> 64) * p;
}
inline int qpow(int a,int b){
	if(b==0) return 1;
	if(b==1) return a;
	int k = qpow(a,b>>1);
	k=o(k*k);
	if(b&1) k=o(k*a);
	return k;
}
int C[MAXN][MAXN];
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0); 
	cin >> n >> m >> c;init(MOD);
	for(register short i=0;i<=400;i++){
		C[i][0]=1;
		for(register short j=1;j<=i;j++){
			C[i][j]=o(C[i-1][j-1]+C[i-1][j]);
		}
	}
	for(register short i = 0;i<=n;i++){
		for(register short j = 0;j<=m;j++){
			for(register short k = 0;k<=c;k++){
				ans = o(ans+o(o(o(o(o((i+j+k)&1?-1:1)*C[n][i])*C[m][j])*C[c][k])*qpow(c-k+1,n*m-i*m-j*n+i*j)));
			}
		}
	}
	cout << o(o(ans)+MOD);
	return 0;
}

tag

洛谷、JSOI、2015、题解
数学、容斥、非正解卡常