组合数学（文章）

组合数学

Part 1. 基础的排列组合

加法原理和乘法原理

1. 加法原理（分类计数原理）：完成一件事，有 \(n\) 类办法，如果在第 \(1\) 类办法中有 \(m_1\) 种不同的方法，在第 \(2\) 类办法中有 \(m_2\) 种不同的方法,…，在第 \(n\) 类办法中有 \(m_n\) 种不同的方法，那么完成这件事共有：\(N＝m_1+m_2+…+m_n\) 种不同的方法。

2. 乘法原理（分步计数原理）：完成一件事，需要分成 \(n\) 个步骤，如果做第 \(1\) 步有 \(m_1\)种不同的方法，做第 \(2\) 步有 \(m_2\) 种不 同的方法，……，做第 \(n\) 步有 \(m_n\) 种不同的方法，那么完成这件事共有：\(N＝m_1×m_2×… ×m_n\) 种不同的方法。

3. 两个原理的区别：一个与分类有关，一个与分步有关；加法原理是“分类完成”，乘法原理是“分步完成”

排列数

排列数：从 \(n\) 个不同元素中取出 \(m\) 个元素排成一列，产生的不同排列数数量为：

\[A_n^m(p_n^m)=\frac{n!}{(n-m)!} \]

类型：

• 条件排列：条件排列是指符合一定条件的排列方案。

  【例如】：将\(1\)、\(2\)、\(3\)、\(4\)、\(5\) 五个数进行排列，要求 \(4\) 一定排在 \(2\) 的前面。问：有多少种排法？

  非常简单。我们可以使用插空法，不过非常麻烦。但是我们再来想一下，在每种方案中如果有 \(2...4\) ，则必定有一种方案是 \(4...2\)，这两种方法 一一对应。所以答案为 \(\frac{A_5^5}{2}=\frac{5!}{2}=60\) 种。

• 相异元素可重排列：从 \(n\) 个不同元素中可以重复地选取出 \(m\) 个元素的排列，叫做相异元素可重复排列。其排列总数为 \(n^m\)。

  【例如】：从 \(1\)、\(2\)、\(3\)、\(4\)、\(5\) 五个数字中任取三个出来组成一个三位数，有 \(A_5^3=60\) 种方案，即一般的排列(每位都不允许相同)。 如果每个数字都可以重复使用（即可以出现 \(111\) 这种三位数），则由乘法原理，有 \(5^3=125\) 种。

• 全排列：把 \(n\) 个元素排成一排的个数。

  【例如】\(A\)，\(B\)，\(C\)，\(D\)，\(E\) 五个人照相，则一共有 \(A_5^5=5!=120\) 种方案。

• 圆排列：从 \(n\) 个不同元素中选取出 \(m\) 个元素，不分首尾地围成一个圆圈的排列叫做圆排列，其排列方案数为：\(\frac{A_n^m}{m}\) 种。

  如果 \(m=n\)，则有 \(\frac{n!}{n}=(n-1)!\)种。

• 错排问题：

  设 \((a_1,a_2,...,a_n)\) 是 \((1,2,...n)\) 的一个全排列，若对于任意的 \(i\in{1,2...,n}\) ,都有 \(a_i≠i\)，则称 \((a_1,a_2,...,a_n)\) 是 \((1,2,...n)\) 的一个错位排列。一般用 \(D_n\) 表示 \((1,2,...n)\) 的错位排列个数。

  \[D_n=n!(1-\frac{1}{1!}+\frac{1}{2!}-...+(-1)^n\frac{1}{n!}) \]

组合数

组合数：从 \(n\) 个不同元素中取出 \(m\) 个元素排成一列（不考虑顺序），产生的排列数量为：

\[C_n^m=\frac{A_n^m}{m!}=\frac{n!}{(n-m)!m!} \]

常用结论：

• \(C_n^m=C_n^{n-m}\)
• \(C_n^m=C_{n-1}^m+C_{n-1}^{m-1}\)
• \(\sum_{i=0}^n C_n^i=2^n\)

二项式定理

二项式定理：

\[(a+b)^n=\sum_{i=0}^n(C_n^ia^{n-i}b^i) \]

康托展开

康托展开：

\[\text{Rank(}\{a_1,a_2,...,a_n\})=\sum_{i=1}^n [(a_i-1-\text{Small}(i-1,a_i))(n-i)!] +1 \]

\(\text{Rank}(k)\) 表示排列 \(k\) 是从小到大第几个排列（排列的排名），\(\text {Small}(n,k)\) 表示前 \(n\) 个中比 \(k\) 小的个数。

next_permutaion 函数的使用方法：

引用头文件： 函数 next_permutaion 在函数库 algorithm里面。

使用方法：和 sort 的参数一样，一般传两个参数，第一个是排列开始的地址，第二个是排列结束的下一个地址，如实现数组第 \(1-3\) 排列的下一个排列：next_permutation(a+1,a+4)。一般作用对象是数组。

作用：next_permutation是求当前排列的下一个排列（按字典序升序的下一个序列），如 1234 的 next_permutation 是1243。在全排列当中经常会用。

C++中next_permutation

抽屉原理

抽屉原理：又叫做鸽巢原理。把 \(n+1\) 件东西放入 \(n\) 个抽屉，则至少有一个抽屉里放了两件或两件以上的东西。从另一个角度说，把 \(n-1\) 件东西放入 \(n\) 个抽屉，则至少有一个抽屉式空的。

例题讲解：

LGP1313[NOIP2011 提高组] 计算系数

题目描述

给定一个多项式 \((by+ax)^k\)，请求出多项式展开后 \(x^n\times y^m\) 项的系数。

输入格式

输入共一行，包含 \(5\) 个整数，分别为 \(a,b,k,n,m\)，每两个整数之间用一个空格隔开。

输出格式

输出共一行，包含一个整数，表示所求的系数。

这个系数可能很大，输出对 \(10007\) 取模后的结果。

样例输入 #1

1 1 3 1 2

样例输出 #1

3

数据范围

对于 \(30\%\) 的数据，有 $ 0\le k\le 10$。

对于 \(50\%\) 的数据，有 $ a=1\(，\)b=1$。

对于 \(100\%\) 的数据，有 \(0\le k\le 1000\)，\(0\le n,m\le k\)，\(n+m=k\)，\(0\le a,b\le 10^6\)。

noip2011 提高组 day2 第 1 题。

【思路分析】

由二项式定理：

\[(ax+by)^k=\sum_{i=0}^k(C_k^ia^{k-i}x^{k-i}b^iy^i) \]

所以，\(x^ny^m\) 的系数为 \(C_k^ma^{k-m}b^m\)。

\(\mathbf{Code}\)：

#include<bits/stdc++.h>
using namespace std;
const int MOD = 10007;
const int MAXN = 1200;
int k,a,b,n,m,p,c[MAXN][MAXN];
int C(int n,int m){
    if(m==0) return 1;
    if(m>n-m) return C(n,n-m);
    if(c[n][m]) return c[n][m];
    return c[n][m] = (C(n-1,m)+C(n-1,m-1))%MOD;
}
int qpow(int a,int b){
    if(b==1) return a;
    if(b==0) return 1;
    int tmp = qpow(a,b/2);
    if(b&1){
        return tmp*tmp%MOD*a%MOD;
    }else{
        return tmp*tmp%MOD;
    }
}
signed main(){
    scanf("%d%d%d%d%d",&a,&b,&k,&n,&m);
    a%=MOD;b%=MOD;
    printf("%d",C(k,m)*qpow(a,k-m)%MOD*qpow(b,m)%MOD);
    return 0;
}

LG1088[NOIP2004 普及组] 火星人

题目描述

人类终于登上了火星的土地并且见到了神秘的火星人。人类和火星人都无法理解对方的语言，但是我们的科学家发明了一种用数字交流的方法。这种交流方法是这样的，首先，火星人把一个非常大的数字告诉人类科学家，科学家破解这个数字的含义后，再把一个很小的数字加到这个大数上面，把结果告诉火星人，作为人类的回答。

火星人用一种非常简单的方式来表示数字――掰手指。火星人只有一只手，但这只手上有成千上万的手指，这些手指排成一列，分别编号为 \(1,2,3,\cdots\)。火星人的任意两根手指都能随意交换位置，他们就是通过这方法计数的。

一个火星人用一个人类的手演示了如何用手指计数。如果把五根手指――拇指、食指、中指、无名指和小指分别编号为 \(1,2,3,4\) 和 \(5\)，当它们按正常顺序排列时，形成了 \(5\) 位数 \(12345\)，当你交换无名指和小指的位置时，会形成 \(5\) 位数 \(12354\)，当你把五个手指的顺序完全颠倒时，会形成 \(54321\)，在所有能够形成的 \(120\) 个 \(5\) 位数中，\(12345\) 最小，它表示 \(1\)；\(12354\) 第二小，它表示 \(2\)；\(54321\) 最大，它表示 \(120\)。下表展示了只有 \(3\) 根手指时能够形成的 \(6\) 个 \(3\) 位数和它们代表的数字：

三进制数	代表的数字
\(123\)	\(1\)
\(132\)	\(2\)
\(213\)	\(3\)
\(231\)	\(4\)
\(312\)	\(5\)
\(321\)	\(6\)

现在你有幸成为了第一个和火星人交流的地球人。一个火星人会让你看他的手指，科学家会告诉你要加上去的很小的数。你的任务是，把火星人用手指表示的数与科学家告诉你的数相加，并根据相加的结果改变火星人手指的排列顺序。输入数据保证这个结果不会超出火星人手指能表示的范围。

输入格式

共三行。
第一行一个正整数 \(N\)，表示火星人手指的数目（\(1 \le N \le 10000\)）。
第二行是一个正整数 \(M\)，表示要加上去的小整数（\(1 \le M \le 100\)）。
下一行是 \(1\) 到 \(N\) 这 \(N\) 个整数的一个排列，用空格隔开，表示火星人手指的排列顺序。

输出格式

\(N\) 个整数，表示改变后的火星人手指的排列顺序。每两个相邻的数中间用一个空格分开，不能有多余的空格。

样例输入 #1

5
3
1 2 3 4 5

样例输出 #1

1 2 4 5 3

数据范围

对于 \(30\%\) 的数据，\(N \le 15\)。

对于 \(60\%\) 的数据，\(N \le 50\)。

对于 \(100\%\) 的数据，\(N \le 10000\)。

noip2004 普及组第 4 题

【思路分析】

我们可以暴力求解下一个排列。

使用 next_permutation。

\(\mathbf{Code}\)：

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 12000;
int n,m,a[MAXN];
signed main(){
    scanf("%d%d",&n,&m);
    for(int i = 1;i<=n;i++){
        scanf("%d",a+i);
    }
    for(int i = 1;i<=m;i++){
        next_permutation(a+1,a+1+n);
    }
    for(int i = 1;i<=n;i++){
        printf("%d ",a[i]);
    }
    return 0;
}

Part 2.容斥原理及应用

引入：

先来看一道很简单的数学题：求不大于 \(20\) 能被 \(2\) 或 \(3\) 整除的正整数个数。

先算出不大于 \(20\) 能被 \(2\) 整除的正整数有 \(10\) 个：\(2,4,6,8,10,12,14,16,18,20\)；

再算出不大于 \(20\) 能被 \(3\) 整除的正整数有 \(6\) 个: \(3,6,9,12,15,18\)。

但是不大于 \(20\) 能被 \(2\) 或 \(3\) 整除的正整数却不是 \(16\) 个，而是 \(13\) 个。原因很简单：因为 \(6,12,18\) 这三个数都计算了两次，重复计算部分必须扣除。

容斥原理：

上面这道题目看似简单的数学题其实就蕴涵了“容斥原理”的精髓。

为了描述容斥原理，通常都要借助集合思想：

假定 \(A\) 和 \(B\) 是集合 \(U\) 的子集：

1. 当 \(A∩B=\empty\) 时 \(|A∪B|=|A|+|B|\)；
2. 当 \(A∩B\neq\empty\) 时 \(|A|+|B|\) 将 \(|A∩B|\) 计算了两次，所以 \(|A∪B|=|A|+|B|-|A∩B|\)。

这便是容斥原理。

容斥原理的定理与推论：

【定理】

令 \(A=A_1\cup A_2\cup A_3\cup...\cup A_m\)，则：

\[\mid A\mid=\sum_{i=1}^m\mid A_i\mid-\sum_{i=1}^m\sum_{j<i}|A_1\cap A_j|+\sum_{i=1}^m\sum_{i<j}\sum_{j<k}\mid A_i\cap A_j\cap A_k\mid+...+(-1)^{m-1}|A_1\cap A_2\cap A_3\cap ...\cap A_m| \]

【推论】

如果 \(A\neq U\) ，且 \(A=A_1\cup A_2\cup A_3\cup...\cup A_m\)，则：

\[\mid \overline A\mid=|I|-\sum_{i=1}^m\mid \overline{A_i}\mid+\sum_{i=1}^m\sum_{j<i}|\overline{A_1}\cap \overline{A_j}|-\sum_{i=1}^m\sum_{i<j}\sum_{j<k}\mid \overline{A_i}\cap \overline{A_j}\cap \overline{A_k}\mid+...+(-1)^{m}|\overline{A_1}\cap \overline{A_2}\cap \overline{A_3}\cap ...\cap \overline {A_m}| \]

例题讲解：

LGP2567 [SCOI2010] 幸运数字

题目背景

四川 NOI 省选 2010。

题目描述

在中国，很多人都把 \(6\) 和 \(8\) 视为是幸运数字！lxhgww 也这样认为，于是他定义自己的“幸运号码”是十进制表示中只包含数字 \(6\) 和 \(8\) 的那些号码，比如 \(68\)，\(666\)，\(888\) 都是“幸运号码”！但是这种“幸运号码”总是太少了，比如在 \([1,100]\) 的区间内就只有 \(6\) 个（\(6\)，\(8\)，\(66\)，\(68\)，\(86\)，\(88\)），于是他又定义了一种“近似幸运号码”。lxhgww 规定，凡是“幸运号码”的倍数都是“近似幸运号码”，当然，任何的“幸运号码”也都是“近似幸运号码”，比如 \(12\)，\(16\)，\(666\) 都是“近似幸运号码”。

现在 lxhgww 想知道在一段闭区间 \([a, b]\) 内，“近似幸运号码”的个数。

输入格式

输入数据是一行，包括 \(2\) 个数字 \(a\) 和 \(b\)。

输出格式

输出数据是一行，包括 \(1\) 个数字，表示在闭区间 \([a, b]\) 内“近似幸运号码”的个数。

样例输入 #1

1 10

样例输出 #1

2

提示

对于 \(30\%\) 的数据，保证 \(1\le a\le b\le10^6\)。

对于 \(100\%\) 的数据，保证 \(1\le a\le b\le10^{10}\)。

【思路分析】

这道题我们先预处理出幸运数个数，总共有 \(2000+\) 多个。当然有些数例如：\(6\)、\(66\) 这样成倍数关系的数，我们只需要保留 \(6\) 即可。筛出来总共有 \(900+\) 个。然后从大到小枚举就行。

\(\mathbf{Code}\)：

#include<bits/stdc++.h>
#define int long long
using namespace std;
int sum,ans;
long long luckynum[2200],a,b;
void Make_Num(long long x){
    if(x>b) return;
    luckynum[++sum] = x;
    // cout << x << endl;
    Make_Num(x*10+6);
    Make_Num(x*10+8);
}
void pre(){
    sum = -1;
    Make_Num(0);
    int tmpsum = 0;
    bool flag[2200] = {0};
    long long tmp[2200] = {};
    sort(luckynum+1,luckynum+1+sum);
    for(int i = 1;i<=sum;i++){
        if(!flag[i]){
            tmp[++tmpsum] = luckynum[i];
            for(int j = i+1;j<=sum;j++){
                if(luckynum[j]%luckynum[i]==0){
                    flag[j] = 1;
                }
            }
        }
    }
    memcpy(luckynum,tmp,sizeof(luckynum));
    // reverse(luckynum+1,luckynum+1+tmpsum);
    sum = tmpsum;
}
long long lcm(long long x,long long y){
    return x*y/__gcd(x,y);
}
void calc(int x,bool y,long long z,long long w){
    long long tmp;
    for(int i = x;i>=1;i--){
        tmp = lcm(z,luckynum[i]);
        if(tmp>0&&tmp<=w){
            if(y){
                ans += w/tmp;
            }else{
                ans -= w/tmp;
            }
            calc(i-1,y^1,tmp,w);
        }
    }
}
long long count(int x){
    if(x<5) return 0;
    ans = 0;
    calc(sum,1,1,x);
    return ans;
}
signed main(){
    scanf("%lld%lld",&a,&b);
    pre();
    printf("%lld",count(b)-count(a-1));
    return 0;
}

Part 3.Catalan 数列

Catalan 数的基本形式

递推公式

\[f_n=\sum_{i=1}^n f_{i-1}\times f_{n-i} ,f_0=f_1=1 \]

组合公式

\[f_n=C_{2n}^n-C_{2n}^{n-1}=\frac{1}{n+1}C_{2n}^n (n\in{1,2,3...}) \]

前 \(7\) 个\(\text{Catalan}\) 数为：\(1,1,2,5,14,42,132,429\)。

衍生例题

【例题1】将 \(n\) 个 \(1\) 和 \(n\) 个 \(-1\) 排成一行，要求对于所有的 \(k(k∈[1,n])\)，第 \(1\) 个数至第 \(k\) 个数的累加和均非负，问有几种排列方法？

【例题2】有 \(2n\) 个人排成一行进入剧场。入场费 \(5\) 元。其中只有 \(n\) 个人有一张 \(5\) 元钞票，另外 \(n\) 人只有 \(10\) 元钞票，剧院无其它钞票，问有多少种方法使得只要有 \(10\) 元的人买票，售票处就有 \(5\) 元的钞票找零？

【例题3】在圆上选择 \(2n\) 个点，将这些点成对连接起来，使得所得到的 \(n\) 条线段不相交的方法数？

【例题4】n*n 的方格地图中，从左下角到右上角，求不跨越对角线的路径条数。

【例题5】给定 n 个结点(结点编号为:1,2,..,n)的二叉树，其中序遍历结果为：1,2,…,n，问具备这种遍历结果的二叉树有几种不同形态？（二叉树形态的计数）

【例题6】对于连乘 \(a_0\times a_1\times a_2\times...\times a_n\)，加了括号后可改变它的运算顺序。问：有多少种不同的运算顺序？（乘法加括号）

【例题7】 一个栈(无穷大)的进栈序列为 \(1,2,3,..n\)，有多少个不同的出栈序列？（出栈次序问题）

公式证明

递推式证明：

以例题 \(7\) 为例：我们每加入一个数我们只能在原本的序列里面插入。例如，在最后一个数入栈之前，已经有 \(i\) 个数已经入栈了，方法数为 \(f_i\)。剩下 \(n-i\) 个数的出站顺序为 \(f_{n-i}\)，我们最后一个数在只能在第 \(i\) 个数出之入栈，又要在第 \(i+1\) 个数之前出栈，所以这是一个方案数固定（方案数为 \(1\)）的情况，所以最后的递推式为 \(f_n=\sum_{i=1}^n f_{i-1}\times f_{n-i}\)。

组合公式证明：

其实我们只需要推出其中一个组合式，另外一个组合数就迎刃而解了，我们正是来证明。

我们拿例题4来详细证明。

先来看一张图：

我们不难发现，要从左下角 \((1,1)\) 到右上角 \((n,n)\)，总共需要走 \(n\) 次向右边走，\(n\) 次向左边走。所以方法总数为 \(C_{2n}^n\) 种方法，但是我们考虑到有这样的这情况在：

emm。所以我们要去掉一些情况，也就是在某一个时刻向上的个数大于向左的个数。这样不好处理，我们可以换一个思考方式，我们将整个图做一个对称：

则问题变成了从七点出发走任意的路径到点 \((n,n-1)\) 的方法数，和上面几乎一样，总共有 \(C_{2n}^{n-1}\) 种方法。

综上所述，\(f_n=C_{2n}^n-C_{2n}^{n-1}\)。最后暴力算一下：

\[\begin{align*} f_n&=C_{2n}^n-C_{2n}^{n-1}\\ &=\frac{(2n)!}{(n!)^2}-\frac{(2n)!}{(n+1)!(n-1)!}\\ &=(2n)!(\frac{1}{n^2\cdot((n-1)!)^2}-\frac{1}{n(n+1)\cdot((n-1)!)^2})\\ &=(\frac{(2n)!}{n((n-1)!)^2})(\frac1{n}-\frac1{n+1})\\ &=\frac{(2n)!}{n((n-1)!)^2}\cdot\frac1{n(n+1)}\\ &=\frac{1}{n+1}(\frac{(2n)!}{n((n-1)!)^2}\cdot\frac1{n})\\ &=\frac1{n+1}\cdot\frac{(2n)!}{(n!)^2}\\ &=\frac1{n+1}\cdot C_{2n}^n \end{align*} \]

得证。

例题讲解：

LGP1044[NOIP2003 普及组] 栈

题目背景

栈是计算机中经典的数据结构，简单的说，栈就是限制在一端进行插入删除操作的线性表。

栈有两种最重要的操作，即 pop（从栈顶弹出一个元素）和 push（将一个元素进栈）。

栈的重要性不言自明，任何一门数据结构的课程都会介绍栈。宁宁同学在复习栈的基本概念时，想到了一个书上没有讲过的问题，而他自己无法给出答案，所以需要你的帮忙。

题目描述

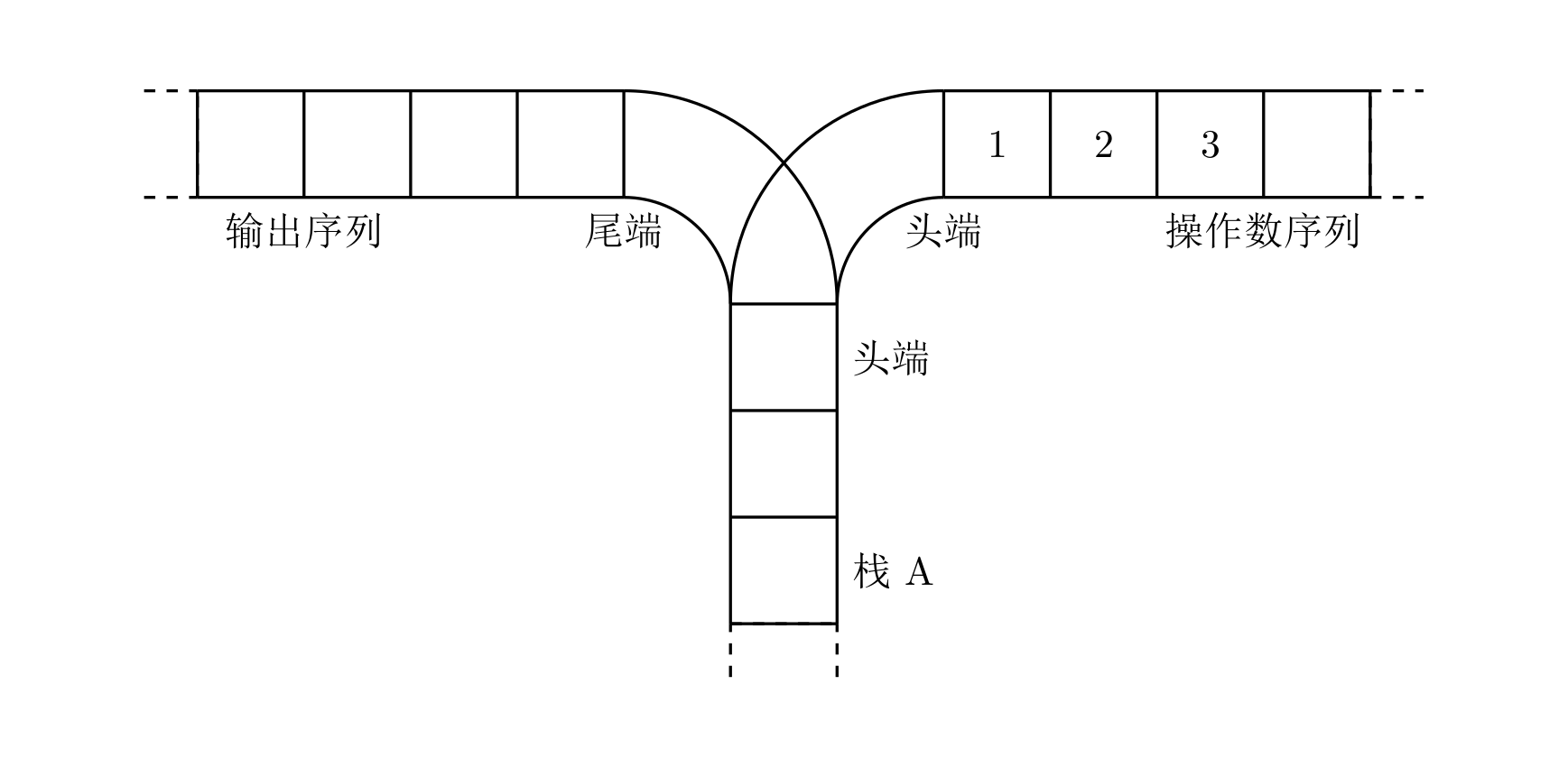
宁宁考虑的是这样一个问题：一个操作数序列，\(1,2,\ldots ,n\)（图示为 1 到 3 的情况），栈 A 的深度大于 \(n\)。

现在可以进行两种操作，

1. 将一个数，从操作数序列的头端移到栈的头端（对应数据结构栈的 push 操作）
2. 将一个数，从栈的头端移到输出序列的尾端（对应数据结构栈的 pop 操作）

使用这两种操作，由一个操作数序列就可以得到一系列的输出序列，下图所示为由 1 2 3 生成序列 2 3 1 的过程。

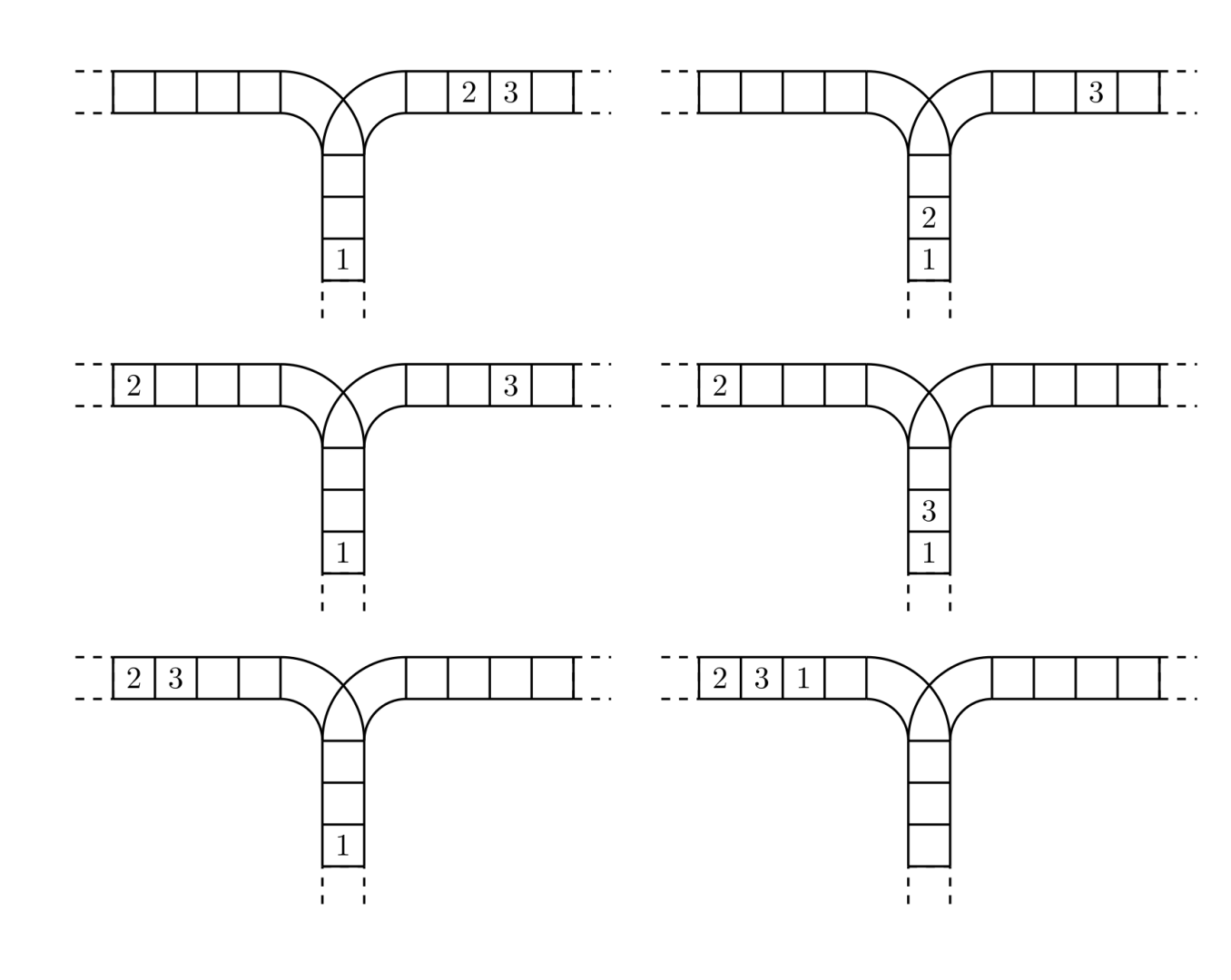
（原始状态如上图所示）

你的程序将对给定的 \(n\)，计算并输出由操作数序列 \(1,2,\ldots,n\) 经过操作可能得到的输出序列的总数。

输入格式

输入文件只含一个整数 \(n\)（\(1 \leq n \leq 18\)）。

输出格式

输出文件只有一行，即可能输出序列的总数目。

样例输入 #1

3

样例输出 #1

5

【题目来源】

NOIP 2003 普及组第三题

【思路分析】

纯的裸的卡特兰数问题。

\(\mathbf{Code}\)：

#include<bits/stdc++.h>
using namespace std;
int n,f[20];
signed main(){
	scanf("%d",&n);
	f[0] = 1;
	f[1] = 1;f[2] = 2;
	for(int i = 3;i<=n;i++){
		for(int k = 1;k<=i;k++){
			f[i]+=f[k-1]*f[i-k];
		}
	}
	printf("%d",f[n]);	
    return 0;
}

Part 4.stirling 数

Stirling 数，又称为斯特灵数。在组合数学，Stirling 数可指两类数，都是由 18 世纪数学家 James Stirling 提出的。

【第一类 Stirling数】是有正负的，其绝对值是包含 \(n\) 个元素的集合分作 \(k\) 个环排列的方法数目。递推公式为：

\(S(n,0)=0,S(1,1)=1\)。

\(S(n,k)=S(n-1,k-1)+(n-1)S(n-1,k)\)。

【第二类Stirling数】是把包含 \(n\) 个不同元素的集合划分为正好 \(k\) 个非空子集的方法的数目。递推公式为：

\[\begin{align} S(n,k)=0 &&(n<k)或(k=0)\\ S(n,k)=S(n-1,k-1)+k\times S(n-1,k)&& 2\le k\le n \end{align} \]

应用：把 \(n\) 个有标号小球放进 \(k\) 个一样的盒子里面，其方案数为 \(S(n,k)\)

例题讲解：

LGP1287 盒子与球

题目描述

现有 \(r\) 个互不相同的盒子和 \(n\) 个互不相同的球，要将这 \(n\) 个球放入 \(r\) 个盒子中，且不允许有空盒子。请求出有多少种不同的放法。

两种放法不同当且仅当存在一个球使得该球在两种放法中放入了不同的盒子。

输入格式

输入只有一行两个整数，分别代表 \(n\) 和 \(r\)。

输出格式

输出一行一个整数代表答案。

样例输入 #1

3 2

样例输出 #1

6

样例输入输出 1 解释

有两个盒子（编号为 \(1, 2\)）和三个球（编号为 \(1, 2, 3\)），共有六种方案，分别如下：

盒子编号	方案 1	方案 2	方案 3	方案 4	方案 5	方案 6
盒子 \(1\)	小球 \(1\)	小球 \(2\)	小球 \(3\)	小球 \(2, 3\)	小球 \(1, 3\)	小球 \(1, 2\)
盒子 \(2\)	小球 \(2, 3\)	小球 \(1, 3\)	小球 \(1, 2\)	小球 \(1\)	小球 \(2\)	小球 \(3\)

数据规模与约定

对于 \(100\%\) 的数据，保证 \(0 \leq r \leq n \leq 10\)，且答案小于 \(2^{31}\)。

【思路分析】

因为盒子不同，所以每个方法的结果分别标号 \(1-n\)，总共有 \(S(n,k)\times k!\)。

\(\mathbf{Code}\)：

#include<bits/stdc++.h>
using namespace std;
int n,r;
int S(int x,int y){
    if(y<0) return 0;
    if(x<y) return 0;
    if(x==y) return 1;
    return S(x-1,y-1)+y*S(x-1,y);
}
int fac(int x){
    if(x<=1) return 1;
    return fac(x-1)*x;
}
signed main(){
    scanf("%d%d",&n,&r);
    printf("%d",S(n,r)*fac(r));
    return 0;
}