数据结构与算法学习笔记
Leetcode笔记
前置的语法:STL
-
C++声明二维数组
int m=grid.size(); int n=grid[0].size(); auto dp = vector < vector <int> > (m, vector <int> (n));或者
//输入vector<int> &triangle vector<vector<int>> dp(triangle.size(),vector<int>(triangle.size(),0));C++里数组长度是用
triangle.size() -
ACM模式处理输入输出
题型一:两数/三数/四数之和:使用散列表/双指针降复杂度
-
第一题:两数之和:从数组中找到两个数使其和为target,返回索引值。
优质解法:利用哈希表优化时间复杂度,以空间换时间把查找时间从O(n)降到O(1)
hashmap:直接查找关键字值的数据结构
-
第15题:三数之和:从数组中找到和为0的三个数的所有不重复组合。
关键技术:双指针
第一个指针first=0,1,……n-3,第二个指针second=first+1,first+2,…… n-2。在第二个指针从左往右走的同时,第三个指针从右往左走,检查两个指针指向的数的和。因为总共走了N步,所以把时间复杂度从\(O(N^2)\)降到了\(O(N)\).(srds python还是过不了)
-
第18题:四数之和
关键技术:哈希表保存所有可能的两数之和
题型二:括号匹配问题:使用栈/动态规划
-
第20题:判断括号是否匹配:左括号入栈,右括号检查栈顶元素是否匹配,若匹配则栈顶出栈。
-
第32题(hard):寻找最长有效括号:
-
栈方法:进栈的元素是下标!
具体实现:1. 初始将-1入栈。2. 遇到左括号将其下标入栈。遇到右括号将栈顶出栈,然后用当前index减去栈顶元素得到最长长度。如果此时栈已经为空,则将右括号下标入栈表示数组已经被该右括号分割。
-
动态规划方法
-
题型三:动态规划方法
-
第九题:数字回文数:判断一个32位的整数是否是回文数
- 如果将数字转变成字符串则空间代价比较大。
- 可以不转换字符串,直接对数字进行操作:反转后半部分的数字,检查是否与前半部分相同。
-
第三题:无重复字符最长子串
- 滑动窗口:利用哈希集合。
-
第990题:等式方程的可满足性
-
并查集
![]()
-
题型四:树相关知识
-
第1379题:找出克隆二叉树中的target结点:同时遍历两棵树。用栈/队列代替递归操作进行遍历。
-
面试题04.10:检查子树:检查T2是否是T1的子树:
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode(int x) : val(x), left(NULL), right(NULL) {} * }; */ class solution{ public: bool checkSubTree(TreeNode*t1,TreeNode*t2){ //判断T2是否是T1的子树 if(t2==NULL) return true; if(t1==NULL) return false; if(t1->val==t2->val){ return checkSubTree(t1->left,t2->left) && checkSubTree(t1->right,t2->right); } if(t1->val!=t2->val){ return checkSubTree(t1->left,t2)||checkSubTree(t1->right,t2); } } } -
1367题:二叉树中的列表:递归
-
144题:前序遍历返回列表:
-
递归:定义全局变量+定义void函数才可以递归调用
class Solution { vector<int> ans; public: void preorder(TreeNode *root){ if(root==NULL) return; ans.push_back(root->val); preorder(root->left); preorder(root->right); } vector<int> preorderTraversal(TreeNode* root) { preorder(root); return ans; } }; -
递归改栈:右子树进栈->左子树进栈->root进栈
class Solution { public: vector<int> preorderTraversal(TreeNode* root) { if(root==NULL) return {}; stack<TreeNode*> s; vector<int> ans; s.push(root); while(!s.empty()){ TreeNode* cur=s.top(); ans.push_back(cur->val); s.pop(); if(cur->right) s.push(cur->right); if(cur->left) s.push(cur->left); } return ans; } };
-
-
dfs:第1315题:求祖父节点为偶数的节点值之和
class Solution { int sum=0; public: void dfs(int grandPa_val,int parent_val,TreeNode* node){ if(node==NULL) return; if(grandPa_val%2==0){ sum+=node->val; } dfs(parent_val,node->val,node->left); dfs(parent_val,node->val,node->right); } int sumEvenGrandparent(TreeNode* root) { dfs(1,1,root); return sum; } };- dfs要定义成void,返回值定义成全局的
- 考虑到要讨论root下两层的节点存在性,可以把原来设计的
dfs(TreeNode* GrandPa, TreeNode* pa,TreeNode* node)改成dfs(int grandpa_val,int parent_val,TreeNode *node),然后把root上面两层设虚拟节点值1。
-
判断是否满足AVL树条件:自底向上递归
对于每一个结点root,先判断其左子树、右子树是否满足AVL条件。如果都满足,那么判断对于root是否满足(类似于后序遍历)
class Solution { public: int height(TreeNode* root) { if (root == NULL) { return 0; } int leftHeight = height(root->left); int rightHeight = height(root->right); if (leftHeight == -1 || rightHeight == -1 || abs(leftHeight - rightHeight) > 1) { return -1; } else { return max(leftHeight, rightHeight) + 1; } } bool isBalanced(TreeNode* root) { return height(root) >= 0; } }; -
根据层次遍历建树,以及求树的层次遍历结果
- 建树
观察层次遍历序列:[0,1,2,null,3],首先根据数组第一个元素创建root,然后将root入队。
每次循环中,将队首节点出队,从遍历到的当前位置往后数两个元素,分别作为当前节点的左子节点和右子节点。然后按顺序将这两个节点也入队。
TreeNode* root;
vector<int> preTraverse;
buildTree(vector<int>& input) {
//输入按层次遍历顺序输入
int n = input.size();
if (n == 0) {
root = NULL;
return;
}
queue<TreeNode*> q;
root = new TreeNode(input[0]);
if (n == 1) return;
q.push(root);
int cur = 1;
while (!q.empty()) {
TreeNode* front = q.front();
q.pop();
if (front == NULL) continue;
int cnt = 0;
while (cur < n && cnt < 2) {
TreeNode* tmp = (input[cur]==null)? NULL:new TreeNode(input[cur]);
cur++;
cnt++;
q.push(tmp);
if (cnt == 1) front->left = tmp;
if (cnt == 2) front->right = tmp;
}
}
}
- 层次遍历
题型五:无序三重循环降复杂度:
-
第1395题:统计作战单位数:给定无序int数组ratings,找到i,j,k,使得i,j,k有序且ratings[i],ratings[j],ratings[k]也有序
关键思路:枚举中间点
class Solution { public: int numTeams(vector<int>& rating) { if(rating.size()<=2) return 0; int cnt=0; for(int j=1;j<rating.size()-1;j++){ //枚举中间点 int leftLess=0; int leftMore=0; int rightLess=0; int rightMore=0; for(int i=0;i<j;i++){ if(rating[i]<rating[j]){ leftLess++; } else if(rating[i]>rating[j]){ leftMore++; } } for(int k=j+1;k<rating.size();k++){ if(rating[k]>rating[j]){ rightMore++; } else if(rating[k]<rating[j]){ rightLess++; } } cnt+=leftLess*rightMore+leftMore*rightLess; } return cnt; } };
题型六:博弈问题:包含先后手转换
但是这种方法经常超时超空间orz---有时间再回去看石子游戏5的题解
面对超时的一些修改办法:
- max,min这种函数自己写
- vector比较慢,改array
- 控制台能运行通过但是commit会超时也真的是rlgl
-
第877题:石子游戏:很多堆石子数组,每次只能拿走最左边或者最右边的一堆;假设两个人都贼精明,求谁嬴谁输。
通用解法:区间dp
-
dp[i][j]定义成在区间piles[i…j]中间的最优解。它是一个元组,包含了(first,second)两个值。dp[i][j].first表示先手在区间中的最大值,dp[i][j].second表示后手在区间中的最大值。 -
状态转移方程:包含先后手转换
![]()
class Solution { public: bool stoneGame(vector<int>& piles) { //dp[i][j][0]表示从piles[i......j],先手获得的最大值 //dp[i][j][1]表示从piles[i......j],后手获得的最大值 //状态转移方程: //dp[i][j][0]=max(piles[i]+dp[i+1][j][1],piles[j]+dp[i][j-1][1]) //dp[i][j][1]= //初始化 //if j==i dp[i][j][0]=piles[i],dp[i][j][1]=0 //if j==i+1 dp[i][j][0]=max(piles[i],piles[i+1]),dp[i][j][1]=min(piles[i],piles[i+1]); //return dp[0][n-1][0]>dp[0][n-1][1] int n=piles.size(); if(n<=2) return true; vector<vector<vector<int>>> dp(n,vector<vector<int>>(n,vector<int>(2,0))); //initialize: for(int i=0;i<n-1;i++){ dp[i][i][0]=piles[i]; dp[i][i][1]=0; dp[i][i+1][0]=max(piles[i],piles[i+1]); dp[i][i+1][1]=min(piles[i],piles[i+1]); } dp[n-1][n-1][0]=piles[n-1]; dp[n-1][n-1][1]=0; for(int i=n-3;i>=0;i--){ for(int j=i+2;j<n;j++){ int left=piles[i]+dp[i+1][j][1]; int right=piles[j]+dp[i][j-1][1]; if(left>right){ //选左边一堆 dp[i][j][0]=left; dp[i][j][1]=dp[i+1][j][0]; } else{ dp[i][j][0]=right; dp[i][j][1]=dp[i][j-1][0]; } } } return dp[0][n-1][0]>dp[0][n-1][1]; } }; -
1147 石子游戏2:字节笔试题:一直debug不出来的动态规划:每次拿X堆,\(1\le X \le 2M\),初始\(M=1\),\(M\)的迭代方程:\(M=max(M,X)\).
#include<vector> #include<iostream> #include<algorithm> using namespace std; int getLarger(double x) { if (x == int(x)) return int(x); else return int(x) + 1; } int stoneGame_2(vector<int>& piles) { //dp方法解答:这可太复杂了 //1.状态定义: //dp[i][j][0]表示从piles[i]开始拿,M=j的情况下先手的最优值 //dp[i][j][1]表示………………后手 //2.状态转移方程: //dp[i][j][0]=max(piles[i]+...+piles[k-1]+dp[k][max(j,k-i)][1]); //dp[i][j][1]=dp[k][max(j,k-i)][0]; //k表示从第i堆拿到第k-1堆,一共拿了X=k-i堆,所以k的范围是[i+1,min(n,i+2j)] //3.初始化条件: //dp[i][ceil((n-i+1)/2)][0]=piles[i]+...+piles[n-1]; //dp[i][ceil((n-i+1)/2)][1]=0 //4.返回值 //return dp[0][1][0] if (piles.size() == 0) return 0; if (piles.size() == 1) return piles[0]; if (piles.size() == 2) return piles[0] + piles[1]; //initialize: int n = piles.size(); vector<vector<vector<int>>> dp(n, vector<vector<int>>(n, vector<int>(2, 0))); for (int i = 0; i < n; i++) { for (int j = getLarger((n - i) / 2.0); j < n; j++) { for (int k = i; k < n; k++) { dp[i][j][0] += piles[k]; } dp[i][j][1] = 0; } } //迭代开始: for (int i = n - 1; i >= 0; i--) { for (int j = 1; j < getLarger((n - i) / 2.0); j++) { dp[i][j][0] = piles[i] + dp[i + 1][1][1]; dp[i][j][1] = dp[i + 1][1][0]; for (int k = i + 1; k < min(n + 1, i + 2 * j + 1); k++) { //getsum int sum = piles[i]; for (int t = i + 1; t < k; t++) sum += piles[t]; if (sum + dp[k][max(j, k - i)][1] > dp[i][j][0]) { dp[i][j][0] = sum + dp[k][max(j, k - i)][1]; dp[i][j][1] = dp[k][max(j, k - i)][0]; } } } } return dp[0][1][0]; } int main() { vector<int> piles; int a[8] = { 2,3,44,4,33,45,100,900 }; piles.insert(piles.begin(), a, a + 8); return stoneGame_2(piles); } //测试样例过一半,如果测试样例为[2,3,44,4,33,45,100,900]则过不了,单步执行发现dp[1][3]=229/900,错了;别的dp值都正常。累了累了 咸了咸了bye
-
题型七:字符串
回文子串
-
第5题:最长回文子串
-
简单的\(O(N^2)\)动态规划算法:
vector<vector<bool>> dp; //dp[i][j]表示s[i...j]是否为回文串 //dp[i][j]=dp[i+1][j-1] && (s[i]==s[j]) -
Manacher算法:在线性时间内求解最长回文子串,一种类似于动态规划的算法,维护一个以每个结点为中心的最长字串长度的数组。
-
预处理:同一奇偶字符串的表示:在原字符串的每一个间隔中插入‘#’,如‘aba’经过预处理以后为‘#a#b#a#’,这样预处理以后的字符串一定是奇数串。
-
定义R为最长子串最右边界,C为回文子串中心(C和R是伴生的),i为当前遍历数组索引,开始遍历。
- i>R,则直接用O(n)的中心拓展算法暴力匹配
- i<R,检查i的回文子串长:利用i关于C的对称点i’。
- i的回文子串长度对应到数组边界不超过R,则不更新
- i的回文子串长度对应到数组边界超过R,更新R,C。
-
class Solution { public: int expand(const string& s, int left, int right) { while (left >= 0 && right < s.size() && s[left] == s[right]) { --left; ++right; } return (right - left - 2) / 2; } string longestPalindrome(string s) { int start = 0, end = -1; string t = "#"; for (char c: s) { t += c; t += '#'; } t += '#'; s = t; vector<int> arm_len; int right = -1, j = -1; for (int i = 0; i < s.size(); ++i) { int cur_arm_len; if (right >= i) { int i_sym = j * 2 - i; int min_arm_len = min(arm_len[i_sym], right - i); cur_arm_len = expand(s, i - min_arm_len, i + min_arm_len); } else { cur_arm_len = expand(s, i, i); } arm_len.push_back(cur_arm_len); if (i + cur_arm_len > right) { j = i; right = i + cur_arm_len; } if (cur_arm_len * 2 + 1 > end - start) { start = i - cur_arm_len; end = i + cur_arm_len; } } string ans; for (int i = start; i <= end; ++i) { if (s[i] != '#') { ans += s[i]; } } return ans; } }; -
重复子串
- 题459:判断一个字符串是否可以由其某一子串重复多次生成:
字符串匹配:KMP算法
https://zhuanlan.zhihu.com/p/83334559
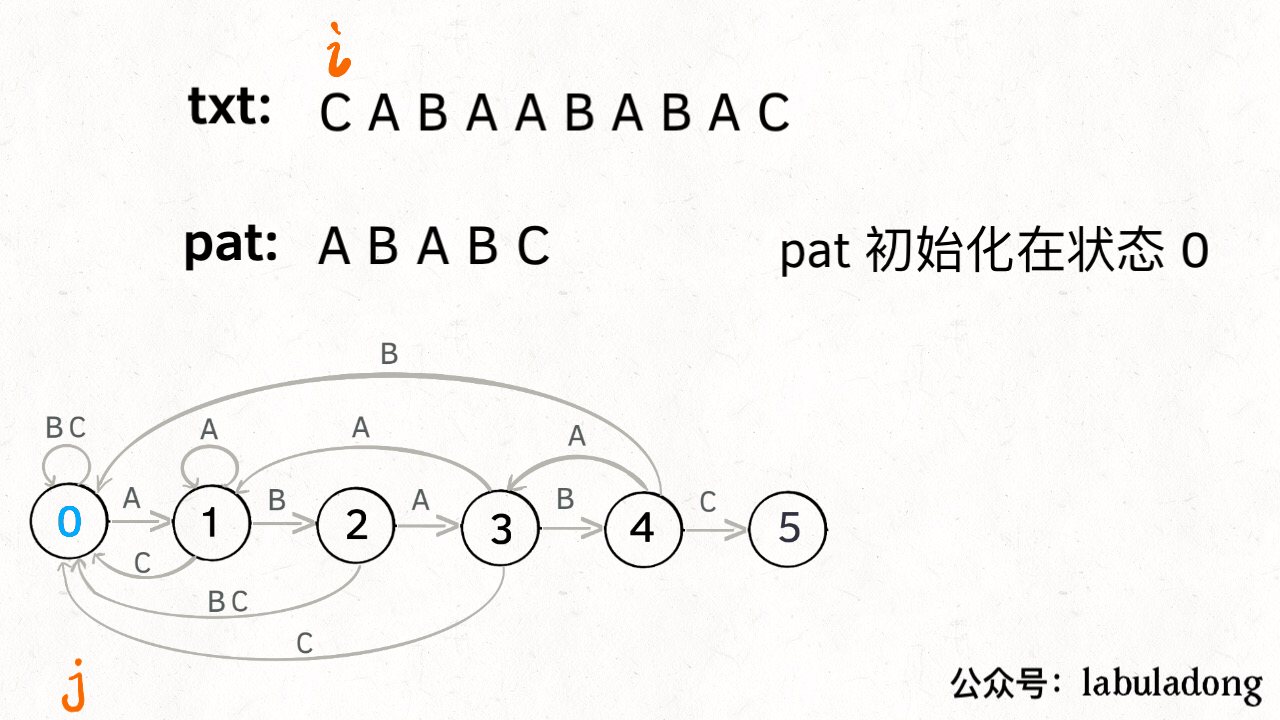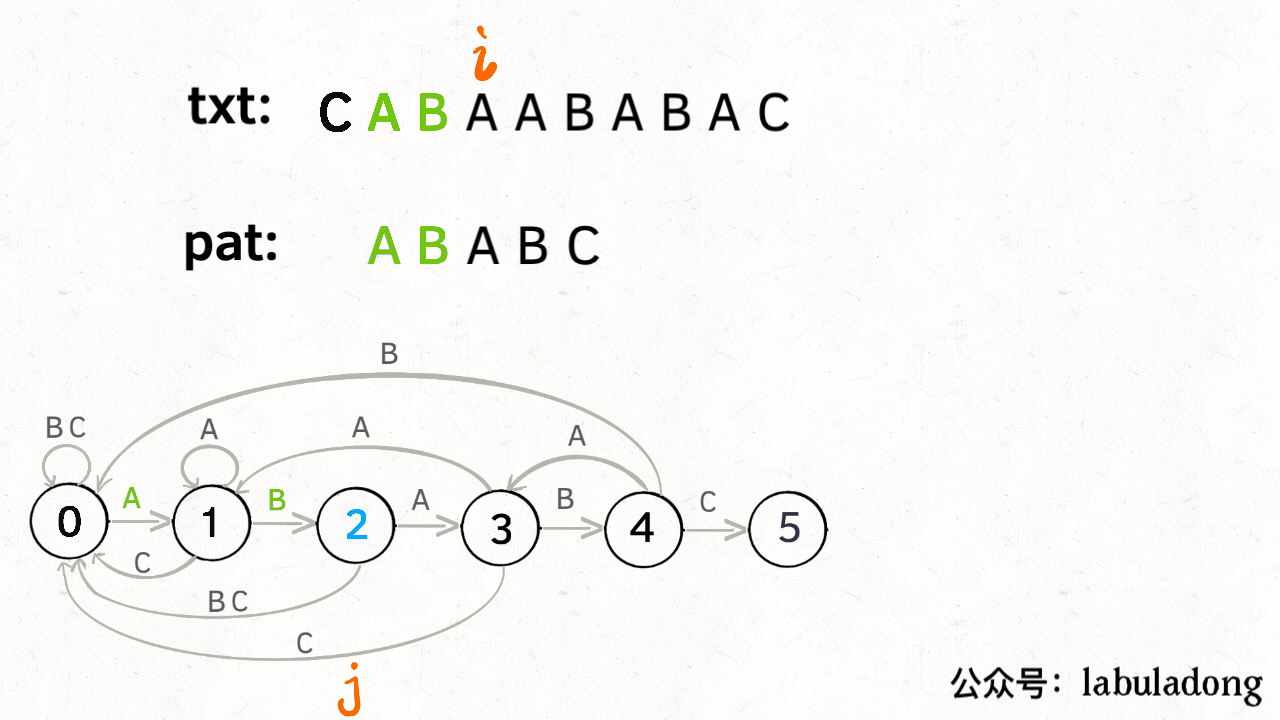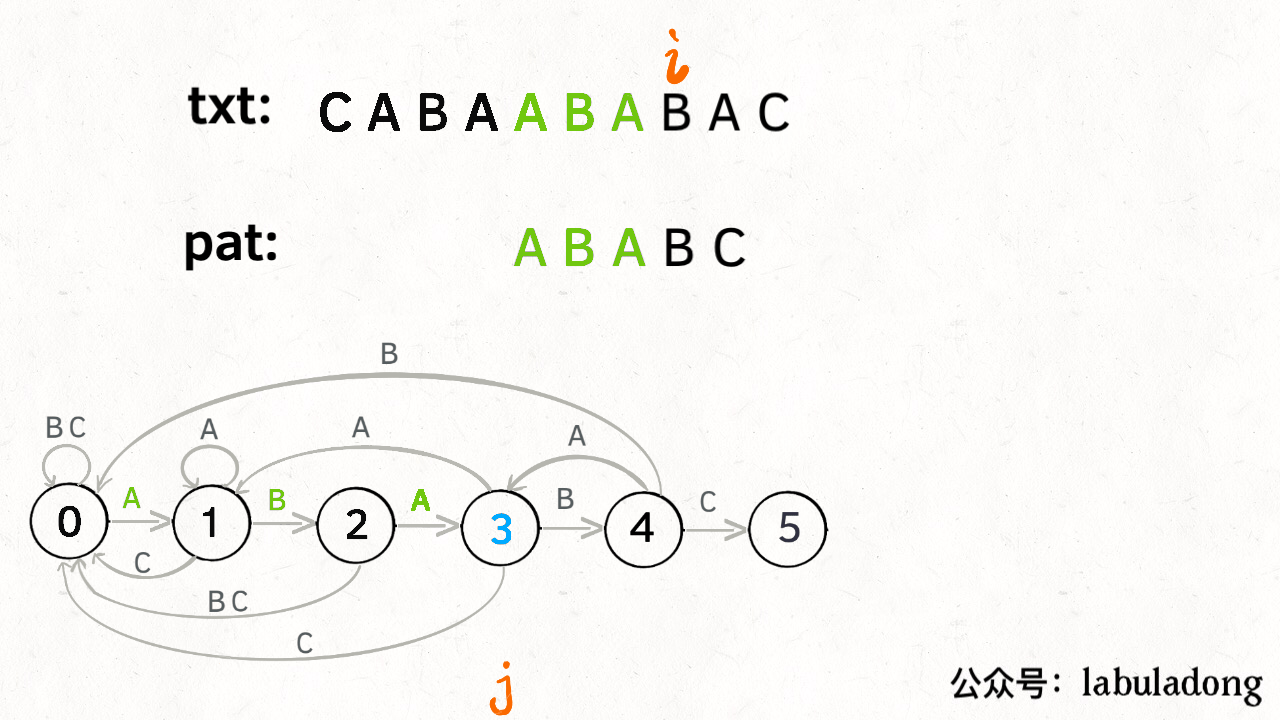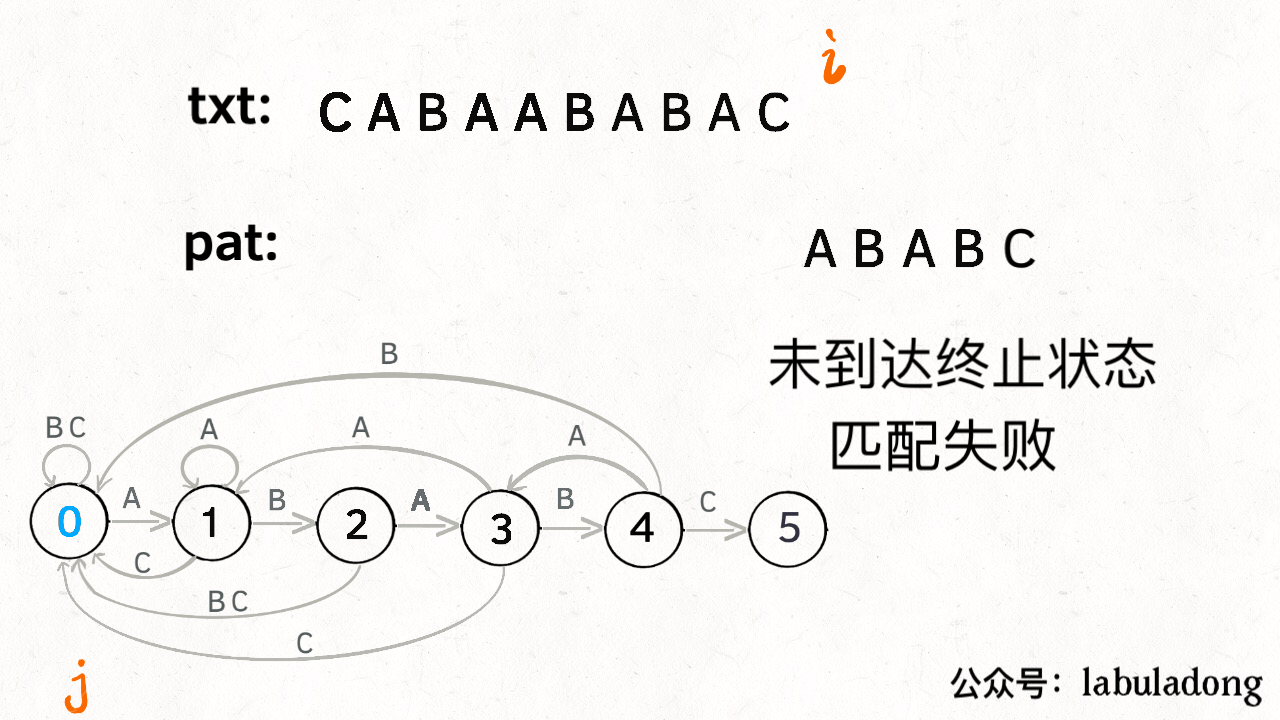
KMP是一种结合了动态规划的字符串匹配算法。长字符串txt中找一个子串pat。利用动态规划dp数组解决暴力匹配中重复计算的问题。
-
dp数组的定义:
dp[j][c] = next 0 <= j < M,代表当前的状态 0 <= c < 256,代表遇到的字符(ASCII 码) 0 <= next <= M,代表下一个状态 dp[4]['A'] = 3 表示: 当前是状态 4,如果遇到字符 A, pat 应该转移到状态 3 dp[1]['B'] = 2 表示: 当前是状态 1,如果遇到字符 B, pat 应该转移到状态 2 -
状态转移方程:
public int search(String txt) { int M = pat.length(); int N = txt.length(); // pat 的初始态为 0 int j = 0; for (int i = 0; i < N; i++) { // 当前是状态 j,遇到字符 txt[i], // pat 应该转移到哪个状态? j = dp[j][txt.charAt(i)]; // 如果达到终止态,返回匹配开头的索引 if (j == M) return i - M + 1; } // 没到达终止态,匹配失败 return -1; } //状态转移伪代码 int X # 影子状态 for 0 <= j < M: for 0 <= c < 256: if c == pat[j]: # 状态推进 dp[j][c] = j + 1 else: # 状态重启 # 委托 X 计算重启位置 dp[j][c] = dp[X][c] -
转移目标的确定:前缀匹配
-
如果下一目标匹配,则向下一目标转移;(状态推进)
-
如果不匹配,就要回退(状态重启)。找到最近的有相同前缀的状态转移之。
public class KMP { private int[][] dp; private String pat; public KMP(String pat) { this.pat = pat; int M = pat.length(); // dp[状态][字符] = 下个状态 dp = new int[M][256]; // base case dp[0][pat.charAt(0)] = 1; // 影子状态 X 初始为 0 int X = 0; // 当前状态 j 从 1 开始 for (int j = 1; j < M; j++) { for (int c = 0; c < 256; c++) { if (pat.charAt(j) == c) dp[j][c] = j + 1; else dp[j][c] = dp[X][c]; } // 更新影子状态 X = dp[X][pat.charAt(j)]; } } public int search(String txt) {...} }
-
波兰表达式
读入一个字符串形式表达的中缀式(正常的运算表达式,可以用二叉树形式理解,叶子节点是数字,非叶节点是运算符号),可以通过栈转化成前缀式(波兰表达式)进行运算。
图算法
始终考虑:
- bfs?dfs?
- 邻接矩阵?邻接表?
- 入度表?出度表?
-
题1557:找最小点集使其可以到达所有点:找入度为0的点即可。
class Solution { public: vector<int> findSmallestSetOfVertices(int n, vector<vector<int>>& edges) { vector<int> indegrees(n,0); for(int i=0;i<edges.size();i++){ int from=edges[i][0]; int to=edges[i][1]; indegrees[to]++; } vector<int> ans; for(int i=0;i<n;i++){ if(indegrees[i]==0) ans.push_back(i); } return ans; } };
拓扑排序:
-
题207:考虑先修课程的课表,判断是否可行
![]()
拓扑排序的时间复杂度是\(O(V(G)+E(G))\).
对于本题的建模:
- 将每一门课看成一个结点
- 如果B是A的先修课,那么从B到A连一条有向边。
- 本题可以约化为判断是否为有向无环图
算法流程:维护一个入度表+BFS
- 统计入度,维护入度表
- 将所有入度为0的结点入队
- 在队列非空时将首节点出队,然后将出队结点指向的结点入度减一。将此时入度为0的结点入队。
- 每次出队时执行
numCourses--,如果出循环时numCourses==0那么return true;
图着色问题:
根据输入的边的条件建邻接表!
-
1042图着色:
class Solution { public: vector<int> gardenNoAdj(int N, vector<vector<int>>& paths) { //涂色问题 //建邻接表 vector<vector<int>> graph(N,vector<int>()); for(int i=0;i<paths.size();i++){ vector<int> cur=paths[i]; graph[cur[0]-1].push_back(cur[1]-1); graph[cur[1]-1].push_back(cur[0]-1); } vector<bool> visited(N,false); vector<int> ans(N); for(int i=0;i<N;i++){ if(visited[i]) continue; set<int> tmpSet; for(int j=0;j<graph[i].size();j++){ int tmpNode=graph[i][j]; tmpSet.insert(ans[tmpNode]); } for(int m=1;m<5;m++){ if(tmpSet.find(m)==tmpSet.end()){ ans[i]=m; } } visited[i]=true; } return ans; } };
最短路径问题:
-
1344题,给定赋权无向图,求阈值范围内最少邻居。(暴力dfs超时)
-
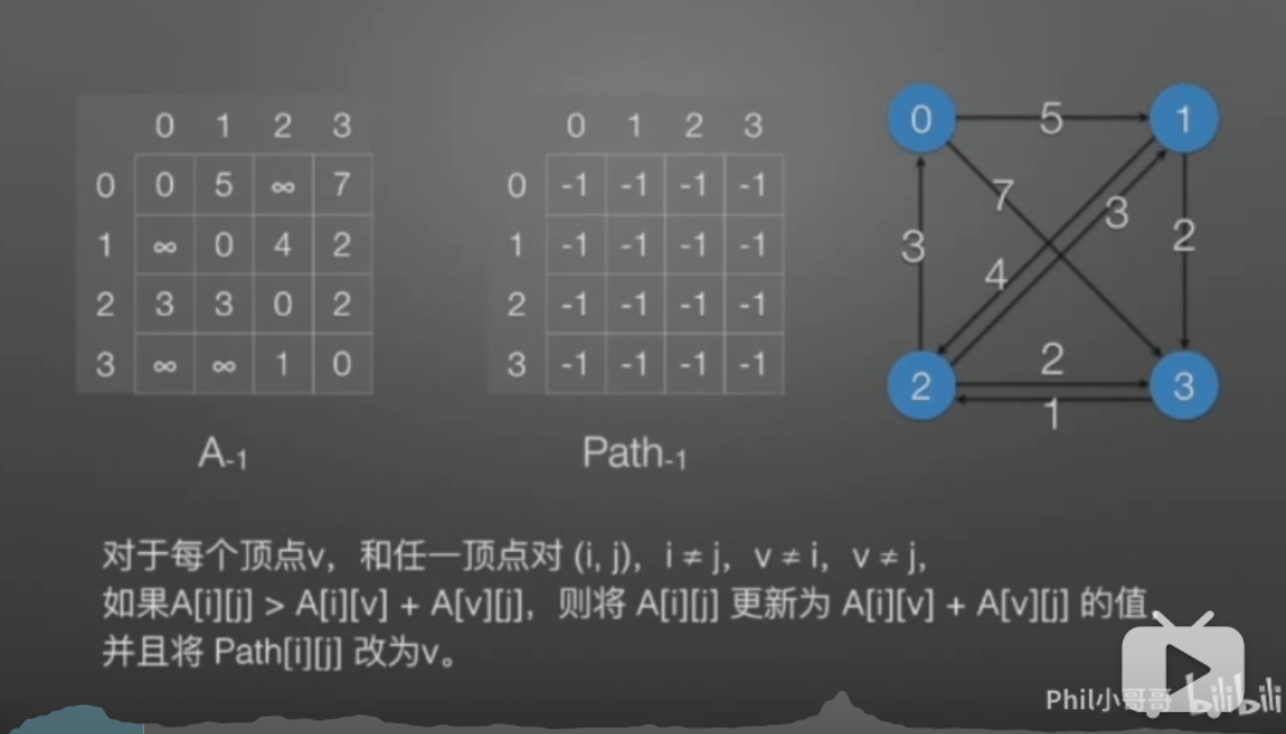
Floyd算法(多源最短路径)
![]()
A中保存当前遍历到的最短路径,Path中保存经过的点;A和Path的下标就是当前v的值
![]()
-
bellman-ford算法:可以用于负权值图
-
Dijkstra算法(单源最短路径):定义已经遍历的结点集S。用bfs(遍历cur_node的所有子节点,然后对每个子节点递归调用bfs)记录最短路径,当遍历到该子节点时将其加入S,然后记录最短路径。
class Solution { protected: int inf = 1e9; vector<vector<int> > MP;//邻接表 public: int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) { vector<vector<int> > mp(n,vector<int>(n,inf)); for(int i = 0; i < edges.size(); i++){ int s = edges[i][0]; int e = edges[i][1]; int w = edges[i][2]; mp[s][e] = w; mp[e][s] = w; mp[s][s] = 0; mp[e][e] = 0; } MP = mp; int ans = inf; int ins = 0; for(int i = n - 1; i >= 0; i--){ int temp = dijkstra(i,distanceThreshold); if(temp < ans){ ans = temp; ins = i; } } return ins; } int dijkstra(int start,int dt){ int n = MP.size(); int sp = start; int counts = 0; vector<int> dis = MP[sp]; vector<int> visited(n); visited[sp] = 1; for(int k = 0; k < n - 1; k++){ int max_dis = inf; int min_index = -1; for(int i = 0 ; i < n; i++){ if(visited[i] == 0 && dis[i] < max_dis){ max_dis = dis[i]; min_index = i; } } if(min_index == -1) break; visited[min_index] = 1; for(int i = 0; i < n; i++){ dis[i] = min(dis[i], dis[min_index] + MP[min_index][i]); } } for(int i = 0; i < n; i++){ if(dis[i] <= dt) counts++; } return counts - 1; } };
-
海陆问题:BFS
-
1162题:地图分析:给定海陆位置,给每块海洋定义一个最短距离为其到陆地的最小距离。找到最大的这个距离。
思路:BFS求每一个海洋的最短路径。这个算法需要维护一个visited数组+一个队列。
int findNearestLand(int x, int y) { memset(vis, 0, sizeof vis); queue <Coordinate> q; q.push({x, y, 0}); vis[x][y] = 1; while (!q.empty()) { auto f = q.front(); q.pop(); for (int i = 0; i < 4; ++i) { int nx = f.x + dx[i], ny = f.y + dy[i]; if (!(nx >= 0 && nx <= n - 1 && ny >= 0 && ny <= m - 1)) continue; if (!vis[nx][ny]) { q.push({nx, ny, f.step + 1}); vis[nx][ny] = 1; if (a[nx][ny]) return f.step + 1; } } } return -1; }回去自己写一下!
-
529题:扫雷游戏
int dx8[8] = { -1,-1,-1,0,0,1,1,1 }; int dy8[8] = { 0,-1,1,-1,1,-1,0,1 }; class pos { public: int x; int y; pos(int x, int y) { this->x = x; this->y = y; } }; class Solution { public: bool isNum(char ch) { return (ch >= '1' && ch <= '9'); } bool isOutOfBound(vector<vector<char>>& board, int x, int y) { return (x<0 || y<0 || x>board.size() - 1 || y>board[0].size() - 1); } int getNext2bombNum(vector<vector<char>>& board, int x, int y) { int cnt = 0; for (int i = 0; i < 8; i++) { int new_x = x + dx8[i]; int new_y = y + dy8[i]; if (isOutOfBound(board, new_x, new_y)) continue; if (board[new_x][new_y] == 'M') cnt++; } return cnt; } void bfs(vector<vector<char>>& board, int x, int y) { if (isOutOfBound(board, x, y)) return; pos cur(x, y); queue<pos> q; q.push(cur); while (!q.empty()) { pos u = q.front(); q.pop(); int ans=getNext2bombNum(board,u.x,u.y); if(ans==0){ board[u.x][u.y] = 'B'; for (int i = 0; i < 8; i++) { int new_x = u.x + dx8[i]; int new_y = u.y + dy8[i]; if (isOutOfBound(board, new_x, new_y) || board[new_x][new_y] == 'B'||isNum(board[new_x][new_y])) continue; else { pos tmp(new_x, new_y); q.push(tmp); } } } else{ for (int i = 0; i < 8; i++) { int new_x = u.x + dx8[i]; int new_y = u.y + dy8[i]; if (isOutOfBound(board, new_x, new_y)) continue; if (board[new_x][new_y] == 'M') { board[u.x][u.y] = '0'+getNext2bombNum(board, u.x, u.y); } else if (board[new_x][new_y] == 'B' || isNum(board[new_x][new_y])) continue; } } } } vector<vector<char>> updateBoard(vector<vector<char>>& board, vector<int>& click) { int x = click[0]; int y = click[1]; if (board[x][y] == 'M') { board[x][y] = 'X'; return board; } if (board[x][y] == 'B' || isNum(board[x][y])) return board; int row = board.size(); int col = board[0].size(); bfs(board, x, y); return board; } };虽然超时但是思路反正就是这个样子(摊手---
检查环
-
无向图检查环:并查集
-
有向图检查环:T802 拓扑排序:如果能用拓扑排序,则说明无环。
但是使用拓扑排序的方法也并不能完全发现环的分量,因为如果环的分量中的结点有到达其它结点的分支,则永远无法用入度为0的方法把其他节点与环分量中的结点区分开来。所以拓扑排序只能判断是否是有环有向图,不能发现分量。
不过T802可以通过把图逆转的方法找到分量。
数学方法
-
异或运算优化:
数学方法就是\(0\bigoplus x=x\)
例题:
哈希表
-
1282题:用户分组
![]()
-
自己实现一个hashmap
字典树
-
基本性质:
- 根节点不包含字符,除根节点外每一个结点都只包含一个字符
- 从根节点到某一节点,路径上经过的字符连接起来为该结点的字符串
- 每个结点的所有子结点包含的字符都不相同
-
实现:
https://leetcode-cn.com/problems/QC3q1f/solution/jian-zhi-offer-2-mian-shi-ti-62-shu-zhon-ykfv/
class Trie{
private:
bool isWord;
vector<Trie*> children;
Trie* searchPrefix(string& prefix) {
Trie* node = this;
for (const char& ch : prefix) {
if (node->children[ch - 'a'] == nullptr) {
return nullptr;
}
node = node->children[ch - 'a'];
}
return node;
}
public:
/** Initialize your data structure here. */
Trie() : isWord(false), children(26, nullptr) {}
/** Inserts a word into the trie. */
void insert(string word) {
Trie* node = this;
for (const char& ch : word) {
if (node->children[ch - 'a'] == nullptr) {
node->children[ch - 'a'] = new Trie();
}
node = node->children[ch - 'a'];
}
node->isWord = true;
}
/** Returns if the word is in the trie. */
bool search(string word) {
Trie* node = this->searchPrefix(word);
return node != nullptr && node->isWord;
}
/** Returns if there is any word in the trie that starts with the given prefix. */
bool startsWith(string prefix) {
Trie* node = this->searchPrefix(prefix);
return node != nullptr;
}
};
并查集(Disjoint Set)
最大作用是检查图是否存在环
-
合并连通分量:然后去扫描没有visited的边,如果两个顶点在同一个集合里那么就存在环。、
-
分立集合的合并:类比森林合并成树,把集合用
parent数组表示出来,类似于把集合用树的形式进行组织。然后合并森林。对于每一个点,合并其parent。
例题:
-
第765题(七夕彩蛋:情侣牵手):想办法交换情侣的位置让每对情侣都能牵手
![]()
-
第684题,冗余连接:图是一棵树加上一条边。删去一条“冗余连接”使图仍然是树。
并查集模板:
int n = 1005; // 节点数量3 到 1000 int father[1005]; // 并查集初始化 void init() { for (int i = 0; i < n; ++i) { father[i] = i; } } // 并查集里寻根的过程 int find(int u) { return u == father[u] ? u : father[u] = find(father[u]); } // 将v->u 这条边加入并查集 void join(int u, int v) { u = find(u); v = find(v); if (u == v) return ; father[v] = u; } // 判断 u 和 v是否找到同一个根,本题用不上 bool same(int u, int v) { u = find(u); v = find(v); return u == v; }本题:题目说是无向图,返回一条可以删去的边,使得结果图是一个有着N个节点的树。如果有多个答案,则返回二维数组中最后出现的边。
那么我们就可以从前向后遍历每一条边,边的两个节点如果不在同一个集合,就加入集合(即:同一个根节点)。
如果边的两个节点已经出现在同一个集合里,说明着边的两个节点已经连在一起了,如果再加入这条边一定就出现环了。
动态规划
与递归思想类似,保存递归中间结果,省去解决重复子问题的时间。
- 第337题 打家劫舍3:二叉树动态规划,如果有直接连线(父子关系)则不能偷。

class Solution {
public:
unordered_map<TreeNode*,int> f,g;
void dfs(TreeNode* o){
if(!o) return;
dfs(o->left);
dfs(o->right);
f[o]=o->val+g[o->left]+g[o->right];
g[o]=max(f[o->left],g[o->left])+max(f[o->right],g[o->right]);
}
int rob(TreeNode* root) {
if(!root) return 0;
dfs(root);
return max(f[root],g[root]);
}
};
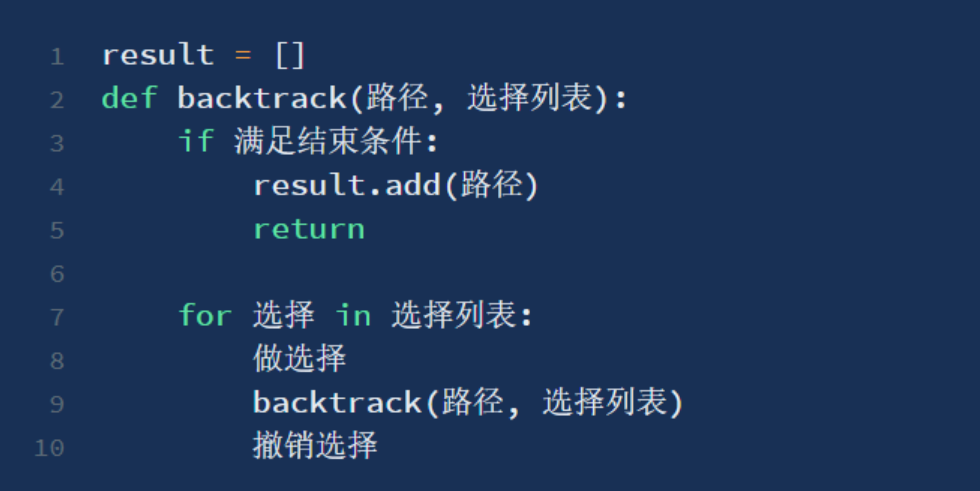
回溯算法:
-
https://labuladong.gitbook.io/algo/di-ling-zhang-bi-du-xi-lie/hui-su-suan-fa-xiang-jie-xiu-ding-ban
![]()
-
第46题:给定无重复数字的数列,返回全排列
搜索回溯:视为插空。定义函数
traceback(first,output)表示以first开头,输出为output的数组class Solution { public: void backtrack(vector<vector<int>>& res, vector<int>& output, int first, int len){ // 所有数都填完了 if (first == len) { res.emplace_back(output); return; } for (int i = first; i < len; ++i) { // 动态维护数组 swap(output[i], output[first]); // 继续递归填下一个数 backtrack(res, output, first + 1, len); // 撤销操作 swap(output[i], output[first]); } } vector<vector<int>> permute(vector<int>& nums) { vector<vector<int> > res; backtrack(res, nums, 0, (int)nums.size()); return res; } };用swap的方法降空间复杂度,减少了一个标记是否已经使用的数组。
二分查找:
二分查找模板:最简单的二分查找:从已排列数组中查找值
bool binary_Search(vector<int>& nums,int target){
int l=0,r=nums.size()-1;
int mid=l+((r-l)>>1);//相当于int mid=(r+l)/2,但可以防止溢出
while(l<r){
if(nums[mid]==target) return true;
else if(nums[mid]>target) r=mid-1;
else l=mid+1;
mid=l+((r-l)>>1);
}
return false;
}
-
题5489,求两球之间磁力(202周赛T3,5分)
class Solution { public: bool check(int x, vector<int>& a, int m) { int cnt = 0; int target = a[0] + x; for(int i = 0; i < a.size() - 1; i++) { if(a[i] < target && a[i + 1] >= target) { cnt++; target = a[i + 1] + x; } } return cnt >= m - 1; } int maxDistance(vector<int>& a, int m) { sort(a.begin(), a.end()); int len = a.size(); int diff = a[len - 1] - a[0]; // 最大间隔 int mn = INT_MAX; // 记录最小间隔 for(int i = 0; i < len - 1; i++) { if(mn > a[i + 1] - a[i]) { mn = a[i + 1] - a[i]; } } if(m == 2) { // 这里特判了m = 2的情况,也可以归到底下的代码中。 return diff; } else { int l = mn, r = diff / (m - 1); // 确定左右边界 while(l <= r) { // 二分搜索 int mid = (l + r) / 2; // printf("l = %d, r = %d, mid = %d\n", l, r, mid); if(check(mid, a, m)) { l = mid + 1; } else { r = mid - 1; } } return l - 1; } } }; -
剑指offer 53-1:排序数组中查找数字出现次数:用两次二分查找确定数字出现的左右边界
滑动窗口
滑动窗口模板
int l=0,r=0,sum=0;
for(;r<n;r++){
sum+=nums[r];
while(DisQualified(sum)){
sum-=nums[l++];
}
//做操作
}
经典例题:在字符串S中寻找包含字符串T的最短子串https://www.bilibili.com/video/BV14Q4y1P7Np?from=search&seid=8825570946872359968
-
例:S=“ABCDEFG”,T=”BD”,开始时滑动窗口为空。当当前窗口包含的字符串不满足要求时,向右扩展。当窗口满足要求时,更新满足要求的最优解,然后左侧加一,继续判断。
-
leetcodeT3:不包含重复字符的最长子串长:滑动窗口,哈希集合维护当前窗口中所有字母。
-
leetcodeT424:替换后的最长重复字符:
example: given "ABBBB",k=1 替换成"BBBBB",return 5解题思路: //双指针维护一个滑动窗口,窗长为start-end+1 //维护一个元素maxSameNum标识当前窗口中所有重复元素的个数中最大的那个 //由于移动过程中最大数目元素字符会变化,用一个数组来表示。 //if maxSameNum+k>=end-start+1,说明可以替换,此时最长的是end-start+1,end右移; //if maxSameNum+k<end-start+1,说明不可以替换,在数组中将start对应的数减一,start右移。 -
leetcode T713,乘积小于k的连续子数组的个数
https://leetcode-cn.com/problems/subarray-product-less-than-k/
class Solution { public: int numSubarrayProductLessThanK(vector<int>& nums, int k) { //滑动窗口 int l=0,r=0; int cur_mul=1; int ans=0; for(;r<nums.size();r++){ cur_mul*=nums[r]; while(cur_mul>=k && l<=r){ cur_mul/=nums[l++]; } //此时固定r,以l,l+1,...r为起点,r为终点的子数组全部满足条件 ans+=r-l+1; } return ans; } };
堆排序
-
普通的堆排序使用语法:
priority_queue<int> heap;//大顶堆 priority_queue<int,vector<int>,greater<int>> heap;//小顶堆 heap.insert(); heap.erase();自定义堆的元素和比较算法:
auto comp = [](const test_heap_data& data1, const test_heap_data& data2) { return data1.val*data1.val < data2.val*data2.val; }; priority_queue<test_heap_data, vector<test_heap_data>, decltype(comp)> q(comp);注意这个comp定义的时候,定义的是将元素放在优先级队列尾的比较算法。所以想要堆顶最小,需要定义>,想要堆顶最大,需要定义<
-
利用堆排序设计算法
-
例T295,数据流的中位数:在插入数据的时候顺便排序,并且输出其中位数。
用两个堆实现:
- 维护一个大顶堆和一个小顶堆,大顶堆中放小的那一半,小顶堆中放大的那一半;小顶堆的堆顶(最小元素)比大顶堆顶堆(最大元素)还要大。
- 如果当前数据总数为奇数,则允许大顶堆比小顶堆多持有一个元素;是偶数则两个堆元素个数相同;
- 插入步骤:维护数据结构
- 插入一个数到大顶堆;
- 将大顶堆堆顶出队,送给小顶堆;
- 如果不满足平衡条件,即小顶堆元素比大顶堆多,则将小顶堆堆顶出队,送给大顶堆。
-
背包问题:
https://www.cnblogs.com/jbelial/articles/2116074.html dd大牛的《背包九讲》
-
0-1背包:
- 问题描述:有一个背包最多载重w,一批物品,分别重w_i,并且有价值v_i。一件物品只能拿一次,求背包最多承载多少价值的物品。
- 状态定义:dp[i][j]表示从下标0...i的物品中任意取,放进总重为j的背包,其中的最大价值
- 递推方程: 方程根据放不放i推出。
- 不放i:dp[i][j]=dp[i-1][j]
- 放i:dp[i][j]=dp[i-1][j-weight[i]]+value[i]
于是,递推方程为:
dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i])
- 初始化:
int n = w.size(); vector<vector<int>> dp(n,vector<int>(w+1,0)); //dp[0][j] for(int j=w[0];j<=w;j++){ dp[0][j]=v[0]; }- 递推:
for(int i=0;i<n;i++){ for(int j=0;j<=w;j++){ dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]) } } return dp[n-1,w];也可以进行降维:dp[i]表示重量为i的背包的最大价值,直接去掉第一维
那么遍历时就有讲究了:for(int j=0;j<n;j++){ for(int i=w;i>=w[j];i--){ dp[i]=max(dp[i],dp[i-w[j]]+v[j]); } }其中j作用是每次都遍历整个数组,确定可以放进来的物品;i从后往前遍历,避免重复。
-
完全背包
- 问题描述:0-1背包的无限版,只需要修改递推关系式和初始化条件就行。
int infinite_package_problem(int w, vector<int>& weight, vector<int>& value) { //dp[i][j]是一样的 //initialize不一样了 //dp[i][j]=max(dp[i-1][j],dp[i][j-weights[i]]+value[i]) int n = weight.size(); vector<vector<int>> dp(n, vector<int>(w+1,0)); for (int j = weight[0];j <= w;j++) { int cur_times = j / weight[0]; dp[0][j] = cur_times * value[0]; } for (int i = 1;i < n;i++) { for (int j = 1;j <= w;j++) { if(j>=weight[i]) dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]); else dp[i][j] = dp[i - 1][j]; } } printDp(dp); return dp[n - 1][w]; } -
多重背包
dp[i][j]=max(dp[i][j-kweight[i]]+kvalue[i]),for k in 1...nums[i]
数位dp
一般是:给定一个闭区间[l,r],求区间内满足条件的数的总数。这个区间可能很大。
可以设f(n)为[0,n]的所有满足条件的个数,则res = f[r]-f[l-1],问题转化为求f(n).
数位dp从树的思想来考虑,将数拆分成位\(a_na_{n-1}...a_2a_1\),从字符串的角度dp。
例如:筛选出[l,r]之间不含有5的数字个数
class digit_dp {
public:
vector<vector<int>> dp;
void init() {
dp.clear();
for (int i = 0;i < MAX_LENGTH;i++) dp.push_back(vector<int>(2, 0));
}
int f1(int x) {
init();
if (x == 0) return 0;
if (x < 0) return -1;
string x_str = to_string(x);
return dfs(0, true, x_str);
}
int dfs(int cur_bit, bool limit,string& x_str) {
if (cur_bit == x_str.length()) return 1;
int ans = 0;
if (!limit) {
ans += 8 * dfs(cur_bit + 1, false, x_str);
}
else {
// 先取x[cur_bit]
int x_cur_bit = x_str[cur_bit] - '0';
if (x_cur_bit!=5) ans += dfs(cur_bit + 1, true, x_str);
if (x_cur_bit>5) ans += dfs(cur_bit + 1, false, x_str)*(x_cur_bit-1);
else ans += dfs(cur_bit + 1, false, x_str)*(x_cur_bit);
}
dp[cur_bit][limit] = ans;
return ans;
}
int problem1(int left, int right) {
// return number of ints in [left,right], which does not contain digit 5
// f(i) expresses problem1(0,i), then
// res = f(right)-f(left-1)
// how to get f(x)?
// x = [a0,a1,....a_{n-1}]
// dp[cur][limit]: [0...cur], number of ints satisfying the request
// limit is a bool variable, standing for whether the cur digit have limitation
// digit i has limitation, only if digit i-1 has limitation && digit i-1 equals a_{i-1}
if (right < 0) return -1;
if (right == 0) return 0;
if (left <= 1) return f1(right);
return f1(right) - f1(left - 1);
}
void test() {
vector<int> testcases = { 8,10,20,100,99,30,10000000 };
for (int i = 0;i < testcases.size();i++) {
cout << f1(testcases[i]) << endl;
}
}
};
机器学习算法
- 题1515(197周赛4,hard):给定一组点的坐标,找一个点使这些点到找到的点的欧几里得距离最小。
位运算
-
题201:给定范围,求范围内所有数按位与的结果,问题转换成求二进制公共前缀
class Solution { public: int rangeBitwiseAnd(int m, int n) { int i=0; while(m!=n){ m>>=1; n>>=1; i++; } return m<<i; } }; -
位运算的基本模型:
-
与运算模型
n&(n-1)//将n的最右一位1置0,非常常用!剑指offer11:求二进制中1的个数(包含补码)
int findNumberOfOne(int n){ int cnt=0; while(n!=0){ n=n&(n-1); cnt++; } return cnt; } -
异或运算模型:
-
翻转某一二进制位,将对应的位与1异或。
-
x^x=0 -
运算律和自反性:
a^b=b^aa^(b^c)=(a^b)^c
-
交换两个数
a=a^b; b=a^b;//b=(a^b)^b=a a=a^b;//a=(a^b)^a=b
-
-
取反运算模型
-
位运算符
~,逻辑运算符! -
变换符号:用补码自身的特性
int num=5; int res=~num+1;//res=-num
-
-
移位运算模型:
- 若左移时舍弃的高位不包含1,则左移乘2,右移除以2。
-
剑指offer:
-
两个栈维护一个单向队列:
- 一个栈用来push_back,一个栈用来pop_front
- 仅当用来pop的栈为空时才把push的栈全塞进去。
class CQueue { public: stack<int> stack1,stack2; CQueue() { while(!stack1.empty()){ stack1.pop(); } while(!stack2.empty()){ stack2.pop(); } } void appendTail(int value) { stack1.push(value); if(stack2.empty()){ while(!stack1.empty()){ int tmp=stack1.top(); stack1.pop(); stack2.push(tmp); } } } int deleteHead() { if(stack2.empty()){ while(!stack1.empty()){ int cur=stack1.top(); stack1.pop(); stack2.push(cur); } } if(stack2.empty()) return -1; int tmp=stack2.top(); stack2.pop(); return tmp; } }; -
不用乘法、循环、条件判断等求\(1+2+...+n\)
-
递归
class Solution { public: int sumNums(int n) { n && (n+=sumNums(n-1)); return n; } };不用逻辑判断的时候就用逻辑运算和短路特性控制代码语句的执行与否;
-
快速乘:二进制展开,俄罗斯农夫算法
把乘数二进制展开,然后移位相加。
-
-
一个二维数组,按行递增、按列递增,查找是否存在某个target值。
从右上角开始搜,走折线。
-
不重复节点值,根据前序和中序结果重建二叉树
根据前序找中间结点,在中序结果中定位中序结点,从而确定左子树和右子树。关键要用好个数相等。
-
旋转序列求最小值:二分查找。
一般输入:[3,4,5,1,2]
容易想到的特例:[2,2,2,2,2]
扑街:[2,1,2,2,2,2]
考试的时候怼测试样例真的好难…
C++ algorithm库的神奇的函数们
-
sort函数:排序
vector<int> v={1,4,2,5,6,3}; sort(v.begin(),v.end());//默认升序 sort(v.begin(),v.end(),greater<int>());//降序 vector<string> strs={"a","aaa","ba","fsfs"}; sort(v.begin(),v.end(),[](const auto& str1,const auto& str2 ){return str1.size()<str2.size();})//按字符串长度从小到大排序 -
accumulate函数:求和,未必是加法操作,可以自定义
前两个参数是范围迭代器,第三个参数是累加初值,第四个参数是执行的操作,默认为加。
using namespace std; vector<int> nums={1,4,2,5,6,3}; int result = accumulate(nums.begin(), nums.end(), 0);//输出求和结果 int multiResult=accumulate(nums.begin(),nums.end(),1,multiplies<int>());//输出求积结果 int self_definedRes=accumulate(nums.begin(),nums.end(),0,[](int acc,int ai){ //acc对应到第三个参数 //ai对应到迭代器中的元素 return acc+max(ai-mid,0); });
刷题经验
- 做题一定要有节奏!比如一道题最多最多半小时,花更多的时间意味着算法写错了,哪怕实现出来了最后也会超时。
- 注意代码行数,超过50行就一定是太冗余了







 浙公网安备 33010602011771号
浙公网安备 33010602011771号