历年蓝桥杯真题解析 | 蓝桥杯2025年省赛B组
欢迎大家订阅我的专栏:算法题解:C++与Python实现!
本专栏旨在帮助大家从基础到进阶 ,逐步提升编程能力,助力信息学竞赛备战!
专栏特色
1.经典算法练习:根据信息学竞赛大纲,精心挑选经典算法题目,提供清晰的代码实现与详细指导,帮助您夯实算法基础。
2.系统化学习路径:按照算法类别和难度分级,从基础到进阶,循序渐进,帮助您全面提升编程能力与算法思维。
适合人群:
- 准备参加蓝桥杯、GESP、CSP-J、CSP-S等信息学竞赛的学生
- 希望系统学习C++/Python编程的初学者
- 想要提升算法与编程能力的编程爱好者
附上汇总贴:历年蓝桥杯真题解析 | 汇总
P12130 移动距离
【题目来源】
洛谷:[P12130 蓝桥杯 2025 省 B] 移动距离 - 洛谷
【题目描述】
小明初始在二维平面的原点,他想前往坐标 \((233, 666)\)。在移动过程中,他只能采用以下两种移动方式,并且这两种移动方式可以交替、不限次数地使用:
- 水平向右移动,即沿着 \(x\) 轴正方向移动一定的距离。
- 沿着一个圆心在原点 \((0, 0)\)、以他当前位置到原点的距离为半径的圆的圆周移动,移动方向不限(即顺时针或逆时针移动不限)。
在这种条件下,他到达目的地最少移动多少单位距离?你只需要输出答案四舍五入到整数的结果。
【输入】
无
【输出】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只需要编写一个程序输出这个整数,输出多余的内容将无法得分。
【解题思路】
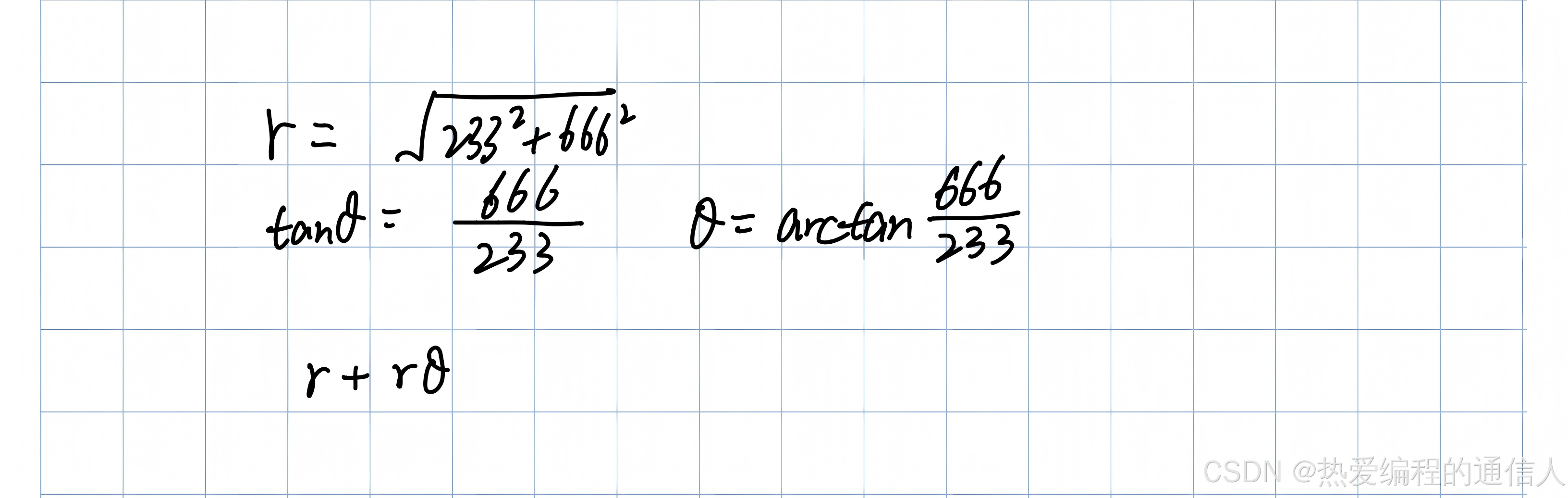
【算法标签】
《洛谷 P12130 移动距离》 #数学# #微积分# #蓝桥杯省赛# #2025#
【代码详解】
#include <bits/stdc++.h>
using namespace std;
double r;
int main()
{
r = sqrt(233 * 233 + 666 * 666); // 计算直角三角形的斜边长度
double theta = atan(1.0 * 666/233); // 计算反正切值,即角度θ
cout << round(r*theta + r) << endl; // 输出计算结果
return 0;
}
【运行结果】
1576
P12131 客流量上限
【题目来源】
洛谷:[P12131 蓝桥杯 2025 省 B] 客流量上限 - 洛谷
【题目描述】
一家连锁旅馆在全国拥有 \(2025\) 个分店,分别编号为 \(1\) 至 \(2025\)。随着节日临近,总部决定为每家分店设定每日客流量的上限,分别记作 \(A_1, A_2, \dots , A_{2025}\)。这些上限并非随意分配,而是需要满足以下约束条件:
- \(A_1, A_2, \dots , A_{2025}\) 必须是 \(1\) 至 \(2025\) 的一个排列,即每个 \(A_i\) 均是 \(1\) 至 \(2025\) 之间的整数,且所有 \(A_i\) 互不相同。
- 对于任意分店 \(i\) 和 \(j\)(\(1 \leq i, j \leq 2025\),\(i\) 可等于 \(j\)),它们的客流量上限 \(A_i\) 和 \(A_j\) 的乘积不得超过 \(i \times j + 2025\)。
这些约束旨在平衡各分店客流压力,确保服务质量和运营稳定性。
现在,请你计算这样的分配方案究竟有多少种。由于答案可能很大,你只需输出其对 \(10^9 + 7\) 取余后的结果即可。
【输入】
无
【输出】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只需要编写一个程序输出这个整数,输出多余的内容将无法得分。
【解题思路】

【算法标签】
《洛谷 P12131 客流量上限》 #组合数学# #蓝桥杯省赛# #2025# #提交答案#
【代码详解】
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int mod = 1e9 + 7;
int ans = 1;
signed main()
{
int t = 2025 / 2; // t = 1012 (整数除法,向下取整)
for (int i = 1; i <= t; i++)
ans = ans * 2 % mod; // 计算2^t mod (1e9+7)
cout << ans << endl;
return 0;
}
【运行结果】
781448427
P12132 可分解的正整数
【题目来源】
洛谷:[P12132 蓝桥杯 2025 省 B] 可分解的正整数 - 洛谷
【题目描述】
定义一种特殊的整数序列,这种序列由连续递增的整数组成,并满足以下条件:
- 序列长度至少为 \(3\)。
- 序列中的数字是连续递增的整数(即相邻元素之差为 \(1\)),可以包括正整数、负整数或 \(0\)。
例如,\([1, 2, 3]\)、\([4, 5, 6, 7]\) 和 \([−1, 0, 1]\) 是符合条件的序列,而 \([1, 2]\)(长度不足)和 \([1, 2, 4]\)(不连续)不符合要求。
现给定一组包含 \(N\) 个正整数的数据 \(A_1, A_2, \dots , A_N\)。如果某个 \(A_i\) 能够表示为符合上述条件的连续整数序列中所有元素的和,则称 \(A_i\) 是可分解的。
请你统计这组数据中可分解的正整数的数量。
【输入】
输入的第一行包含一个正整数 \(N\),表示数据的个数。
第二行包含 \(N\) 个正整数 \(A_1, A_2, \dots , A_N\),表示需要判断是否可分解的正整数序列。
【输出】
输出一个整数,表示给定数据中可分解的正整数的数量。
【输入样例】
3
3 6 15
【输出样例】
3
【解题思路】

【算法标签】
《洛谷 P12132 可分解的正整数》 #数学# #蓝桥杯省赛# #2025#
【代码详解】
#include <bits/stdc++.h>
using namespace std;
int ans;
int n;
int main()
{
cin >> n; // 输入n
for (int i = 1; i <= n; i++)
{
int x; cin >> x; // 输入x
if (x != 1) ans++; // 如果x不等于1,计数器加1
}
cout << ans << endl; // 输出结果
return 0;
}
【运行结果】
3
3 6 15
3
P12133 产值调整
【题目来源】
洛谷:[P12133 蓝桥杯 2025 省 B] 产值调整 - 洛谷
【题目描述】
偏远的小镇上,三兄弟共同经营着一家小型矿业公司“兄弟矿业”。公司旗下有三座矿山:金矿、银矿和铜矿,它们的初始产值分别用非负整数 \(A\)、\(B\) 和 \(C\) 表示。这些矿山的产出是小镇经济的核心,支撑着三兄弟和许多矿工家庭的生计。
然而,各矿山的产值波动剧烈,有时金矿收益高而银矿、铜矿低迷,有时则相反。这种不稳定性让公司收入难以预测,也常引发兄弟间的争执。为了稳定经营,三兄弟设计了一个公平的产值调整策略,每年执行一次,每次调整时,将根据当前的产值 \(A\)、\(B\)、\(C\),计算新产值:
- 金矿新产值:\(A'=\lfloor \dfrac{B+C}{2} \rfloor\);
- 银矿新产值:\(B'=\lfloor \dfrac{A+C}{2} \rfloor\);
- 铜矿新产值:\(C'=\lfloor \dfrac{A+B}{2} \rfloor\);
其中,\(\lfloor \rfloor\) 表示向下取整。例如,\(\lfloor 3.7\rfloor = 3\),\(\lfloor 5.2\rfloor = 5\)。
计算出 \(A'\)、\(B'\)、\(C'\) 后,同时更新:\(A\) 变为 \(A'\),\(B\) 变为 \(B'\),\(C\) 变为 \(C'\),作为下一年调整的基础。
三兄弟认为这个方法能平衡产值波动,于是计划连续执行 \(K\) 次调整。现在,请你帮他们计算,经过 \(K\) 次调整后,金矿、银矿和铜矿的产值分别是多少。
【输入】
输入的第一行包含一个整数 \(T\),表示测试用例的数量。
接下来的 \(T\) 行,每行包含四个整数 \(A,B,C,K\),分别表示金矿、银矿和铜矿的初始产值,以及需要执行的调整次数。
【输出】
对于每个测试用例,输出一行,包含三个整数,表示经过 \(K\) 次调整后金矿、银矿和铜矿的产值,用空格分隔。
【输入样例】
2
10 20 30 1
5 5 5 3
【输出样例】
25 20 15
5 5 5
【算法标签】
《洛谷 P12133 产值调整》 #模拟# #蓝桥杯省赛# #2025#
【代码详解】
#include <bits/stdc++.h>
using namespace std;
int T;
int main()
{
cin >> T; // 输入测试用例数量
while (T--)
{
int a, b, c, k;
cin >> a >> b >> c >> k; // 输入初始值和迭代次数
for (int i = 1; i <= k; i++)
{
// 更新规则:每个数变成另外两个数的平均值
int aa = (b + c) / 2; // a_new = floor((b + c) / 2)
int bb = (a + c) / 2; // b_new = floor((a + c) / 2)
int cc = (a + b) / 2; // c_new = floor((a + b) / 2)
a = aa, b = bb, c = cc; // 同时更新
// 如果三个数相等,提前终止
if (a == b && b == c)
break;
}
cout << a << " " << b << " " << c << endl;
}
return 0;
}
【运行结果】
2
10 20 30 1
25 20 15
5 5 5 3
5 5 5
P12134 画展布置
【题目来源】
洛谷:[P12134 蓝桥杯 2025 省 B] 画展布置 - 洛谷
【题目描述】
画展策展人小蓝和助理小桥为即将举办的画展准备了 \(N\) 幅画作,其艺术价值分别为 \(A_1, A_2, \dots , A_N\)。他们需要从这 \(N\) 幅画中挑选 \(M\) 幅,并按照一定顺序布置在展厅的 \(M\) 个位置上。如果随意挑选和排列,艺术价值的变化可能会过于突兀,导致观众的观展体验不够流畅。
为了优化布置,他们查阅了《画展布置指南》。指南指出,理想的画展应使观众在欣赏画作时,艺术价值的过渡尽量平缓。指南建议,选择并排列 \(M\) 幅画,应使艺术价值的变化程度通过一个数值 \(L\) 来衡量,且该值越小越好。数值 \(L\) 的定义为:
其中 \(B_i\) 表示展厅第 \(i\) 个位置上画作的艺术价值。
现在,他们希望通过精心挑选和排列这 \(M\) 幅画作,使 \(L\) 达到最小值,以提升画展的整体协调性。请你帮他们计算出这个最小值是多少。
【输入】
输入共两行。
第一行包含两个正整数 \(N\) 和 \(M\),分别表示画作的总数和需要挑选的画作数量。
第二行包含 \(N\) 个正整数 \(A_1, A_2, \dots , A_N\),表示每幅画作的艺术价值。
【输出】
输出一个整数,表示 \(L\) 的最小值。
【输入样例】
4 2
1 5 2 4
【输出样例】
3
【算法标签】
《洛谷 画展布置》 #数学# #排序# #前缀和# #双指针two-pointer# #蓝桥杯省赛# #2025#
【代码详解】
#include <bits/stdc++.h>
using namespace std;
#define int long long // 将int重定义为long long
int n, m, a[100005], ans = 1e16; // n: 数字个数, m: 需要选取的数字个数, a: 存储数字, ans: 答案
signed main() // 由于#define int long long,需要使用signed main
{
cin >> n >> m; // 输入数字个数n和需要选取的数字个数m
for (int i = 1; i <= n; i++)
cin >> a[i]; // 读入n个数字
sort(a + 1, a + n + 1); // 对数组进行升序排序
// 寻找最小值
for (int i = m; i <= n; i++) // 遍历可能的子数组终点
{
int j = i - m + 1; // 计算子数组起点
int t = a[i] * a[i] - a[j] * a[j]; // 计算当前子数组的最大最小值平方差
ans = min(t, ans); // 更新最小值
}
cout << ans << endl; // 输出答案
return 0;
}
【运行结果】
4 2
1 5 2 4
3



 浙公网安备 33010602011771号
浙公网安备 33010602011771号