GESP认证C++编程真题解析 | 202403 七级
欢迎大家订阅我的专栏:算法题解:C++与Python实现!
本专栏旨在帮助大家从基础到进阶 ,逐步提升编程能力,助力信息学竞赛备战!
专栏特色
1.经典算法练习:根据信息学竞赛大纲,精心挑选经典算法题目,提供清晰的代码实现与详细指导,帮助您夯实算法基础。
2.系统化学习路径:按照算法类别和难度分级,从基础到进阶,循序渐进,帮助您全面提升编程能力与算法思维。
适合人群:
- 准备参加蓝桥杯、GESP、CSP-J、CSP-S等信息学竞赛的学生
- 希望系统学习C++/Python编程的初学者
- 想要提升算法与编程能力的编程爱好者
附上汇总帖:GESP认证C++编程真题解析 | 汇总
编程题
P10378 七级
【题目来源】
洛谷:[P10378 GESP202403 七级] 交流问题 - 洛谷
【题目描述】
来自两所学校 \(A\)、\(B\) 的 \(n\) 名同学聚在一起相互交流。为了方便起见,我们把这些同学从 \(1\) 至 \(n\) 编号。他们共进行了 \(m\) 次交流,第 \(i\) 次交流中,编号为 \(u_i, v_i\) 的同学相互探讨了他们感兴趣的话题,并结交成为了新的朋友。
由于这次交流会的目的是促进两校友谊,因此只有不同学校的同学之间会交流。同校同学并不会互相交流。
作为 \(A\) 校顾问,你对 \(B\) 校的规模非常感兴趣,你希望求出 \(B\) 校至少有几名同学、至多有几名同学。
【输入】
第一行两个正整数,表示同学的人数 \(n\)、交流的次数 \(m\)。
接下来 \(m\) 行,每行两个整数 \(u_i, v_i\),表示一次交流。
【输出】
输出一行两个整数,用单个空格隔开,分别表示 \(B\) 校至少有几名同学、至多有几名同学。
【输入样例】
4 3
1 2
2 3
4 2
【输出样例】
1 3
【算法标签】
《洛谷 P10378 交流问题》 #搜索# #图论# #并查集# #图论建模# #二分图# #GESP# #2024#
【代码详解】
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5; // 最大节点数
int n, m, s, t; // n: 节点数, m: 边数, s,t: 边的两个端点
int ans1, ans2; // ans1: 最小染色数, ans2: 最大染色数
int num[3]; // num[1]: 颜色1的节点数, num[2]: 颜色2的节点数
int col[N]; // 每个节点的颜色,0表示未染色
vector<int> e[N]; // 邻接表存储图
// 深度优先搜索进行二分图染色
void dfs(int u)
{
// 遍历节点u的所有邻居节点v
for (auto v : e[u])
{
// 如果邻居节点v还未染色
if (col[v] == 0)
{
// 将v染成与u不同的颜色
// 如果col[u]=1,则col[v]=2;如果col[u]=2,则col[v]=1
col[v] = 3 - col[u];
num[col[v]]++; // 对应颜色的节点数加1
dfs(v); // 递归染色v的邻居
}
}
}
int main()
{
// 输入节点数和边数
cin >> n >> m;
// 输入边,构建无向图
for (int i = 1; i <= m; i++)
{
cin >> s >> t;
e[s].push_back(t);
e[t].push_back(s);
}
// 遍历所有节点
for (int i = 1; i <= n; i++)
{
// 如果节点i还未染色,说明找到一个新的连通分量
if (col[i] == 0)
{
// 初始化当前连通分量的颜色计数
num[1] = 1; // 从颜色1开始,所以num[1]=1
num[2] = 0; // 颜色2初始为0
// 将节点i染成颜色1
col[i] = 1;
// 从节点i开始进行DFS染色
dfs(i);
// 统计当前连通分量的结果
// ans1: 最小化颜色1和颜色2的较小值
// ans2: 最大化颜色1和颜色2的较大值
ans1 += min(num[1], num[2]);
ans2 += max(num[1], num[2]);
}
}
// 输出结果
cout << ans1 << " " << ans2 << endl;
return 0;
}
【运行结果】
4 3
1 2
2 3
4 2
1 3
P10379 俄罗斯方块
【题目来源】
洛谷:[P10379 GESP202403 七级] 俄罗斯方块 - 洛谷
【题目描述】
小杨同学用不同种类的俄罗斯方块填满了一个大小为 \(n \times m\) 的网格图。
网格图由 \(n \times m\) 个带颜色方块构成。小杨同学现在将这个网格图交给了你,请你计算出网格图中俄罗斯方块的种类数。
如果两个同色方块是四连通(即上下左右四个相邻的位置)的,则称两个同色方块直接连通;若两个同色方块同时与另一个同色方块直接或间接连通,则称两个同色方块间接连通。一个俄罗斯方块由一个方块和所有与其直接或间接连接的同色方块组成。定义两个俄罗斯方块的种类相同当且仅当通过平移其中一个俄罗斯方块可以和另一个俄罗斯方块重合;如果两个俄罗斯方块颜色不同,仍然视为同一种俄罗斯方块。
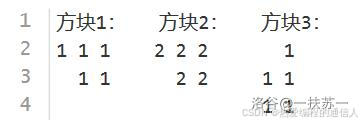
例如,在如下情况中,方块 \(1\) 和方块 \(2\) 是同一种俄罗斯方块,而方块 \(1\) 和方块 \(3\) 不是同一种俄罗斯方块。
【输入】
第一行包含两个正整数 \(n\) 和 \(m\),表示网格图的大小。
对于之后的 \(n\) 行,第 \(i\) 行包含 \(m\) 个正整数 \(a_{i1}, a_{i2}, \dots a_{im}\),表示该行 \(m\) 个方块的颜色。
【输出】
输出一行一个整数表示答案。
【输入样例】
5 6
1 2 3 4 4 5
1 2 3 3 4 5
1 2 2 3 4 5
1 6 6 7 7 8
6 6 7 7 8 8
【输出样例】
7
【算法标签】
《洛谷 P10379 俄罗斯方块》 #模拟# #搜索# #GESP# #2024#
【代码详解】
#include <bits/stdc++.h>
using namespace std;
const int N = 505;
int n, m, k, s, t, sx, sy; // n,m: 网格大小, sx,sy: 当前连通块的起始点
int a[N][N]; // 存储网格中的值
int ans; // 结果,不同形状的数量
int vis[N][N]; // 访问标记数组
// 四个方向的偏移量:右、下、左、上
int d[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
vector<pair<int, int>> e; // 存储当前连通块中所有点的相对坐标
set<vector<pair<int, int>>> se; // 存储所有不同形状的连通块
// 深度优先搜索,用于寻找连通块
void dfs(int x, int y)
{
// 将当前点的相对坐标(相对于连通块起始点)存入向量e
e.push_back({x - sx, y - sy});
// 标记当前点已访问
vis[x][y] = 1;
// 遍历四个方向
for (int i = 0; i < 4; i++)
{
int xx = x + d[i][0]; // 新的x坐标
int yy = y + d[i][1]; // 新的y坐标
// 检查新坐标是否有效
if (xx >= 1 && xx <= n && yy >= 1 && yy <= m && // 在网格范围内
a[xx][yy] == a[x][y] && // 值相同
!vis[xx][yy]) // 未访问过
{
dfs(xx, yy); // 继续深度优先搜索
}
}
}
int main()
{
// 输入网格大小
cin >> n >> m;
// 输入网格数据
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
cin >> a[i][j];
}
}
// 遍历整个网格
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
// 如果当前点未访问过
if (!vis[i][j])
{
// 记录连通块的起始点
sx = i;
sy = j;
// 从当前点开始深度优先搜索,找到整个连通块
dfs(i, j);
// 将当前连通块的形状(相对坐标向量)插入集合
// 集合会自动去重
se.insert(e);
// 清空向量,为下一个连通块做准备
e.clear();
}
}
}
// 输出不同形状的数量
cout << se.size() << endl;
return 0;
}
【运行结果】
5 6
1 2 3 4 4 5
1 2 3 3 4 5
1 2 2 3 4 5
1 6 6 7 7 8
6 6 7 7 8 8
7



 浙公网安备 33010602011771号
浙公网安备 33010602011771号