AtCoder Beginner Contest竞赛题解 | AtCoder Beginner Contest 441
欢迎大家订阅我的专栏:算法题解:C++与Python实现!
本专栏旨在帮助大家从基础到进阶 ,逐步提升编程能力,助力信息学竞赛备战!
专栏特色
1.经典算法练习:根据信息学竞赛大纲,精心挑选经典算法题目,提供清晰的代码实现与详细指导,帮助您夯实算法基础。
2.系统化学习路径:按照算法类别和难度分级,从基础到进阶,循序渐进,帮助您全面提升编程能力与算法思维。
适合人群:
- 准备参加蓝桥杯、GESP、CSP-J、CSP-S等信息学竞赛的学生
- 希望系统学习C++/Python编程的初学者
- 想要提升算法与编程能力的编程爱好者
附上汇总帖:AtCoder Beginner Contest竞赛题解 | 汇总
A - Black Square
【题目来源】
洛谷:[AT_abc441_a ABC441A] Black Square - 洛谷
【题目描述】
There is a grid with \(10^{100}\) rows and \(10^{100}\) columns.
有一个 \(10^{100}\) 行 \(10^{100}\) 列网格。
In what follows, the cell at the \(i\) -th row from the top and \(j\) -th column from the left is denoted as cell \((i,j)\) .
在下文中,从上往下第 \(i\) 行、从左往右第 \(j\) 列的单元格将记为单元格 \((i,j)\)。
In this grid, only the $ 100\times 100 $ region with cell $ (P,Q) $ as the top-left cell is painted black, and all other cells are painted white.
在此网格中,仅以单元格 \((P, Q)\) 为左上角的 \(100\times 100\) 区域被涂为黑色,其余所有单元格均被涂为白色。
Determine whether cell \((X,Y)\) is painted black.
判断单元格 \((X, Y)\) 是否被涂为黑色。
【输入】
The input is given from Standard Input in the following format:
\(P\) \(Q\) \(X\) \(Y\)
【输出】
If cell \((X,Y)\) is painted black, print Yes; otherwise, print No.
【输入样例】
3 3
5 10
【输出样例】
Yes
【代码详解】
#include <bits/stdc++.h>
using namespace std;
int p, q, x, y;
int main()
{
// 输入
cin >> p >> q >> x >> y;
// 检查点(x,y)是否在矩形内
if (x >= p && x <= p + 100 - 1 && y >= q && y <= q + 100 - 1)
cout << "Yes" << endl; // 点在矩形内
else
cout << "No" << endl; // 点在矩形外
return 0;
}
【运行结果】
3 3
5 10
Yes
B - Two Languages
【题目来源】
洛谷:[AT_abc441_b ABC441B] Two Languages - 洛谷
【题目描述】
The AtCoder country has two official languages: Takahashi-go and Aoki-go.
AtCoder 国有两种官方语言:高桥语和青木语。
Both Takahashi-go and Aoki-go use some lowercase English letters to write words in those languages. Takahashi-go uses only the characters contained in a string \(S\) of length \(N\) , and Aoki-go uses only the characters contained in a string \(T\) of length \(M\) .
高桥语和青木语都使用一些小写英文字母来书写其语言的单词。高桥语仅使用长度为 \(N\) 的字符串 \(S\) 中所包含的字符,而青木语仅使用长度为 \(M\) 的字符串 \(T\) 中所包含的字符。
You are given \(Q\) words \(w _ 1,w _ 2,\ldots,w _ Q\) that are in the official languages of the AtCoder country. For each word, determine which of the following applies based on the characters contained in that word:
给定 \(Q\) 个属于 AtCoder 国官方语言的单词 \(w _ 1,w _ 2,\ldots,w _ Q\)。对于每个单词,根据其包含的字符,判断下列哪一种情况适用:
- It is confirmed to be a word in Takahashi-go
确认该单词属于高桥语。 - It is confirmed to be a word in Aoki-go
确认该单词属于青木语。 - Neither can be determined
无法确定属于哪一种语言。
【输入】
The input is given from Standard Input in the following format:
\(N\) \(M\) \(S\) \(T\) \(Q\) \(w _ 1\) \(w _ 2\) \(\vdots\) \(w _ Q\)
【输出】
Print $ Q $ lines. The $ i $ -th line should contain Takahashi if it is confirmed that $ w _ i $ is a word in Takahashi-go, Aoki if it is confirmed to be a word in Aoki-go, and Unknown if neither can be determined.
【输入样例】
6 5
ahikst
aikot
5
asahi
okita
kiai
hash
it
【输出样例】
Takahashi
Aoki
Unknown
Takahashi
Unknown
【算法标签】
《洛谷 AT_abc441_b Two Languages》 #字符串# #枚举#
【代码详解】
#include <bits/stdc++.h>
using namespace std;
int n, m, q;
string s, t;
int main()
{
// 输入
cin >> n >> m >> s >> t >> q;
// 处理q个查询
while (q--)
{
string w; // 查询字符串
cin >> w;
bool f1 = true; // 标志1:w的所有字符是否都在s中
bool f2 = true; // 标志2:w的所有字符是否都在t中
// 检查w的所有字符是否都在s中
for (int i = 0; i < w.size(); i++)
{
bool flag1 = false; // 标记当前字符是否在s中找到
for (int j = 0; j < s.size(); j++)
{
if (w[i] == s[j]) // 如果字符在s中找到
{
flag1 = true;
break; // 找到就退出内层循环
}
}
if (!flag1) // 如果当前字符不在s中
{
f1 = false; // 整个字符串w不满足条件1
break; // 可以提前退出,但这里没有break,会继续检查后面的字符
}
}
// 检查w的所有字符是否都在t中
for (int i = 0; i < w.size(); i++)
{
bool flag2 = false; // 标记当前字符是否在t中找到
for (int j = 0; j < t.size(); j++)
{
if (w[i] == t[j]) // 如果字符在t中找到
{
flag2 = true;
break; // 找到就退出内层循环
}
}
if (!flag2) // 如果当前字符不在t中
{
f2 = false; // 整个字符串w不满足条件2
break; // 可以提前退出,但这里没有break
}
}
// 根据结果输出
if (f1 == true && f2 == false) // 所有字符都在s中,但至少一个不在t中
{
cout << "Takahashi" << endl;
continue;
}
if (f1 == false && f2 == true) // 所有字符都在t中,但至少一个不在s中
{
cout << "Aoki" << endl;
continue;
}
// 其他情况
cout << "Unknown" << endl;
}
return 0;
}
【运行结果】
6 5
ahikst
aikot
5
asahi
Takahashi
okita
Aoki
kiai
Unknown
hash
Takahashi
it
Unknown
C - Sake or Water
【题目来源】
洛谷:[AT_abc441_c ABC441C] Sake or Water - 洛谷
【题目描述】
有 \(N\) 个杯子,每个杯子都装有一种无色透明的液体。
具体来说,第 \(i\) 个杯子 \((1\leq i\leq N)\) 中有 \(A_i\) 毫升液体。
众所周知,这些杯子中正好有 \(K\) 个装的是清酒(米酒),其余的装的是水。但是,不知道哪些杯子装的是清酒。高桥可以选择一些(一个或多个)杯子,喝掉其中的所有液体。
求无论哪些杯子装有清酒,在保证他至少喝 \(X\) 毫升清酒的前提下,他至少需要选择多少个杯子? 如果无法选择,请输出 \(-1\) 。
【输入】
输入内容由标准输入提供,格式如下:
\(N\) \(K\) \(X\)
\(A_1\) \(A_2\) \(\ldots\) \(A_N\)
【输出】
打印高桥为满足条件而需要选择的最少杯子数。如果无法选择,则输出 \(-1\) 。
【输入样例】
3 2 5
10 6 8
【输出样例】
2
【解题思路】
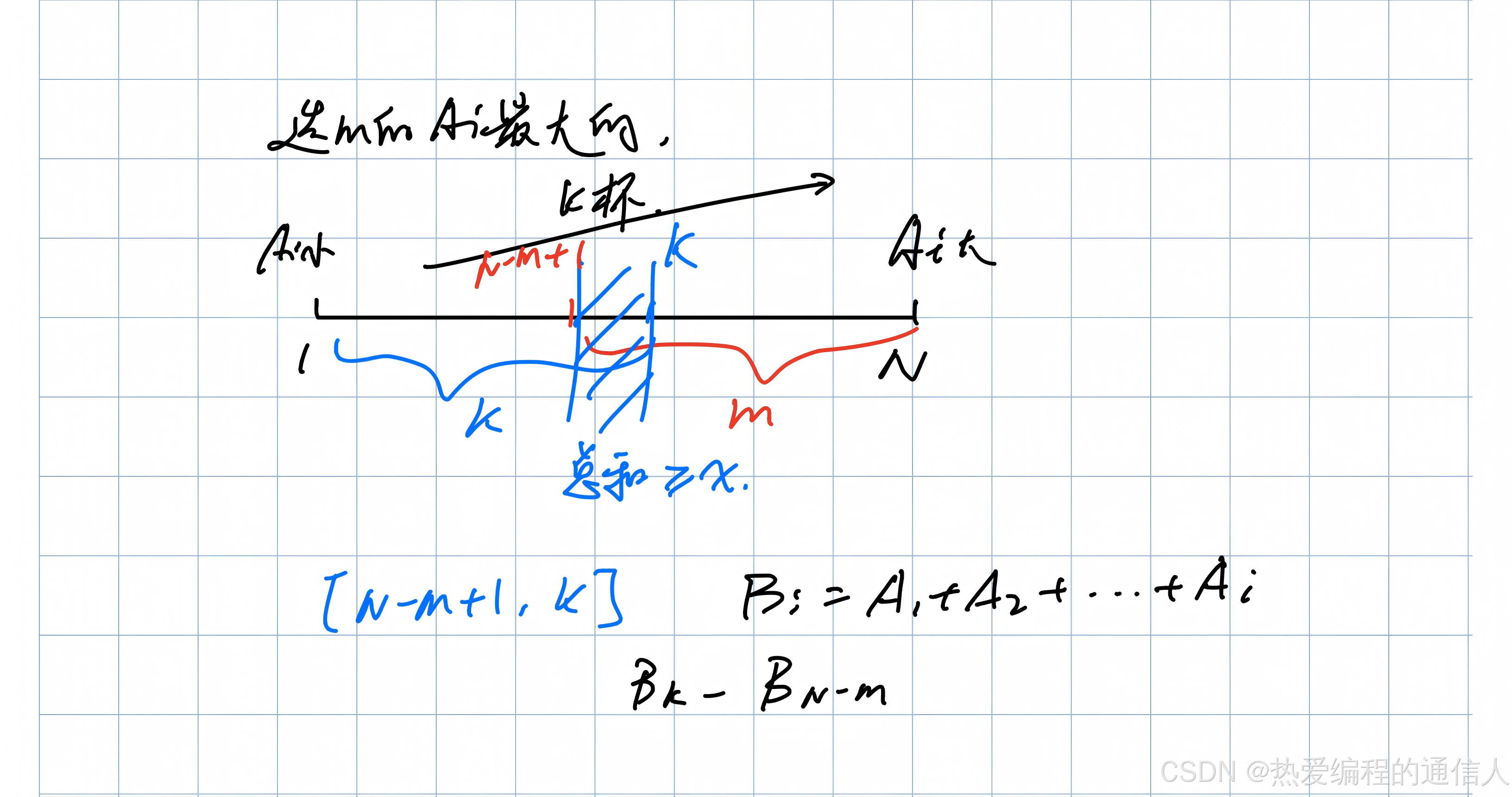
【算法标签】
《洛谷 AT_abc441_c Sake or Water》 #贪心#
【代码详解】
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 300005;
int n, k, x;
int a[N], sa[N]; // a: 原始数组, sa: 前缀和数组
signed main()
{
// 输入
cin >> n >> k >> x;
// 读取数组
for (int i = 1; i <= n; i++)
cin >> a[i];
// 对数组排序(升序)
sort(a + 1, a + n + 1);
// 计算前缀和
for (int i = 1; i <= n; i++)
sa[i] = sa[i - 1] + a[i];
// 调试输出
// for (int i=1; i<=n; i++)
// cout << sa[i] << " ";
// cout << endl;
int ans = -1; // 初始化为-1,表示没找到
// 遍历所有可能的i
for (int i = 1; i <= n; i++) {
// 计算sum = 最大的k个元素和 - 最小的i个元素和
int sum = sa[k] - sa[n - i];
if (sum >= x) { // 如果sum大于等于x
ans = i; // 记录答案
break; // 找到就退出
}
}
cout << ans << endl;
return 0;
}
【运行结果】
3 2 5
10 6 8
2
D - Paid Walk
【题目来源】
洛谷:[AT_abc441_d ABC441D] Paid Walk - 洛谷
【题目描述】
There is a directed graph (not necessarily simple) with \(N\) vertices and \(M\) edges, where the vertices are numbered as vertices \(1, 2, \ldots, N\) .
有一个包含 \(N\) 个顶点和 \(M\) 条边的有向图(不一定是简单图),其中顶点被编号为顶点 \(1, 2, …, N\)。
The \(i\) -th \((1\leq i\leq M)\) edge goes from vertex \(U_i\) to vertex \(V_i\) with cost \(C_i\) . Additionally, the out-degree of each vertex is at most \(4\) .
第 \(i\) 条边 \((1\leq i\leq M)\) 从顶点 \(U_i\) 指向顶点 \(V_i\),其边权为 \(C_i\)。此外,每个顶点的出度至多为 \(4\)。
Find all vertices \(v\) \((1\leq v\leq N)\) that satisfy the following condition:
找出所有满足以下条件的顶点 \(v\) \((1\leq v\leq N)\) :
There exists a path from vertex \(1\) to vertex \(v\) that satisfies both of the following conditions:
存在一条从顶点 \(1\) 到顶点 \(v\) 的路径,该路径满足以下两个条件:
- It traverses exactly \(L\) edges. If the same edge is traversed multiple times, each traversal is counted.
该路径恰好经过 \(L\) 条边。如果同一条边被经过多次,则每次经过都会被计数。- The sum of the costs of the traversed edges is at least \(S\) and at most \(T\) . (If the same edge is traversed multiple times, the cost is added to the sum each time.)
经过的边的边权之和至少为 \(S\) 且至多为 \(T\)。(如果同一条边被经过多次,则每次经过时其边权都会被加入总和。)
What is out-degree? The out-degree of vertex \(u\) refers to the number of edges going out from vertex \(u\) . Even if multiple edges go to the same vertex, they are counted separately.
什么是出度?顶点 \(u\) 的出度指的是从顶点 \(u\) 出发的边的数量。即使有多条边指向同一个顶点,它们也会被分别计数。
【输入】
The input is given from Standard Input in the following format:
\(N\) \(M\) \(L\) \(S\) \(T\) \(U_1\) \(V_1\) \(C_1\) \(U_2\) \(V_2\) \(C_2\) \(\vdots\) \(U_M\) \(V_M\) \(C_M\)
【输出】
Print the vertices that satisfy the condition in ascending order, separated by spaces.
If there are no vertices that satisfy the condition, print an empty line.
【输入样例】
5 8 3 80 100
1 2 20
1 3 70
2 1 30
2 5 10
3 2 10
3 4 30
3 5 20
5 1 70
【输出样例】
1 5
【算法标签】
《洛谷 AT_abc411_d Paid Walk》 #搜索# #图论#
【代码详解】
#include <bits/stdc++.h>
using namespace std;
const int N = 200005, M = 200005;
int n, m, L, S, T;
int h[N], e[M], w[M], ne[M], idx, ans[N];
// 添加有向边
void add(int a, int b, int c)
{
e[idx] = b; // 边的终点
w[idx] = c; // 边的权重
ne[idx] = h[a]; // 下一条边的索引
h[a] = idx++; // 头指针指向新边
}
// 深度优先搜索
void dfs(int u, int l, int val)
{
if (l > L || val > T) return; // 剪枝:超过长度限制或值超过上限
if (l == L) // 达到指定长度L
{
if (val >= S) // 值满足下限要求
ans[u] = 1; // 标记节点u为可行终点
return;
}
// 遍历u的所有出边
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i]; // 邻居节点
dfs(j, l + 1, val + w[i]); // 递归搜索
}
}
int main()
{
// 输入
cin >> n >> m >> L >> S >> T;
// 初始化邻接表
memset(h, -1, sizeof(h));
// 读入m条边
for (int i = 1; i <= m; i++)
{
int u, v, w;
cin >> u >> v >> w;
add(u, v, w); // 添加有向边
}
// 从节点1开始DFS
dfs(1, 0, 0);
// 输出所有可行的终点节点
for (int i = 1; i <= n; i++)
if (ans[i])
cout << i << " ";
cout << endl;
return 0;
}
【运行结果】
5 8 3 80 100
1 2 20
1 3 70
2 1 30
2 5 10
3 2 10
3 4 30
3 5 20
5 1 70
1 5



 浙公网安备 33010602011771号
浙公网安备 33010602011771号