历年CSP-J初赛真题解析 | 2025年CSP-J初赛
欢迎大家订阅我的专栏:算法题解:C++与Python实现!
本专栏旨在帮助大家从基础到进阶 ,逐步提升编程能力,助力信息学竞赛备战!
专栏特色
1.经典算法练习:根据信息学竞赛大纲,精心挑选经典算法题目,提供清晰的代码实现与详细指导,帮助您夯实算法基础。
2.系统化学习路径:按照算法类别和难度分级,从基础到进阶,循序渐进,帮助您全面提升编程能力与算法思维。
适合人群:
- 准备参加蓝桥杯、GESP、CSP-J、CSP-S等信息学竞赛的学生
- 希望系统学习C++/Python编程的初学者
- 想要提升算法与编程能力的编程爱好者
附上汇总贴:历年CSP-J初赛真题解析 | 汇总_热爱编程的通信人的博客-CSDN博客
单项选择
第1题
一个32位无符号整数可以表示的最大值,最接近下列哪个选项?( )
A.\(4×10^9\)
B.\(3×10^{10}\)
C.\(2×10^9\)
D.\(2×10^{10}\)
【答案】:A
【解析】
32位无符号整数最大值\(=2^{32}-1=4,294,967,295\approx 4.3×10^9\)
第2题
在C++中,执行int x =255; cout <<(x & (x - 1)); 后,输出的结果是?( )
A.255
B.254
C.128
D.0
【答案】:A
【解析】
x = 255, x-1=254,x &(x - 1) = 255 & 254 = 254
第3题
函数calc(n)的定义如下,则calc(5)的返回值是多少?( )
int calc(int n) {
if (n <= 1) return 1;
if (n % 2 == 0) return calc(n / 2) + 1;
else return calc(n - 1) + calc(n - 2);
}
A.5
B.6
C.7
D.8
【答案】:B
【解析】
calc(5): return calc(4) + calc(3)
calc(4): return calc(2) + 1
calc(3): return calc(2) + calc(1)
calc(2): return calc(1) + 1
calc(1): return 1
计算:calc(1) = 1, calc(2) = 2, calc(3) = 3, calc(4) = 3, calc(5) = 6
第4题
用5个权值10、12、15、20、25构造哈夫曼树,该树的带权路径长度是多少?( )
A.176
B.186
C.196
D.206
【答案】:B
【解析】
权值10,12,15,20,25;构造哈夫曼树:
合并10,12→22
合并15,20→35
合并22,25→47
合并35,47→82
带权路径长度:10×3+12×3+15×2++20×2+25×2=186
第5题
在一个有向图中,所有顶点的入度之和等于所有顶点的出度之和,这个总和等于?( )
A.顶点数
B.边数
C.顶点数+边数
D.顶点数*2
【答案】:B
【解析】
在有向图中,所有顶点入度之和 = 所有顶点出度之和 = 边数
第6题
从5位男生和4位女生中选出4人组成一个学习小组,要求学习小组中男生和女生都有。有多少种不同的选举方法?( )
A.126
B.121
C.120
D.100
【答案】:C
【解析】
从9人中选4人且男女都有:C(9, 4) = 126
只选男生:C(5, 4) = 5
只选女生:C(4, 4) = 1
男女都有:126 - 5 - 1 = 120
第7题
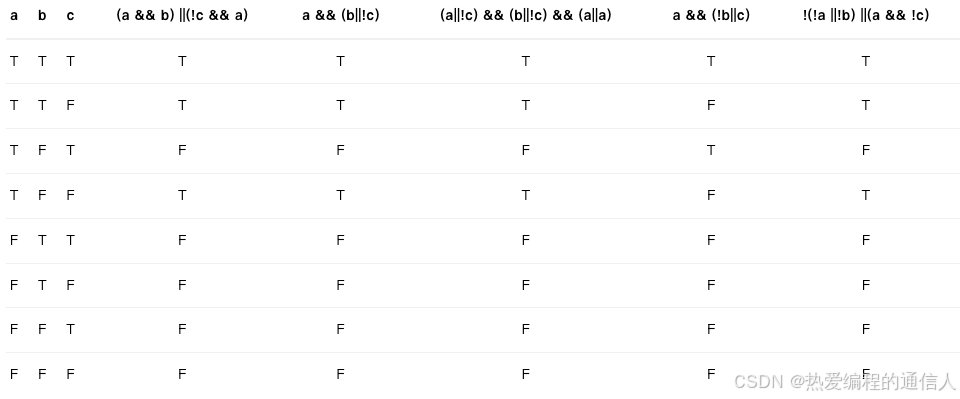
假设a,b,c都是布尔变量,逻辑表达式(a && b)) || (!c && a)的值与下列哪个表达式不始终相等?( )
A.a && (b || !c)
B.(a || !c) && (b || !c) && (a || a)
C.a && (!b || c)
D.!(!a Ⅱ !b) || (a && !c)
【答案】:C
【解析】
假设a,b,c的真假,代入计算选C
第8题
已知f[0]=1,f[1]=1,并且对于所有n≥2有f[n]=(f[n-1]+f[n-2])%7,那么f[2025]的值是多少?
A.2
B.4
C.5
D.6
【答案】:D
【解析】
计算前几项,f[0]=1, f[1] = 1, f[2] = 2, f[3] = 3, f[4] = 5, f[5] = 1, f[6] = 6, f[7] = 0, f[8] = 6,继续计算会发现这是一个周期序列,周期长度为16。
f[2025%16] = f[9] = 6
第9题
下列关于C++ string 类的说法,正确的是?
A.string 对象的长度在创建后不能改变。
B.可以使用+运算符直接连接一个 string 对象和一个 char 类型的字符。
C.string的length()和size()方法返回的值可能不同。
D.string对象必须以'\0'结尾,且这个结尾符计入 length()。
【答案】:B
【解析】
A.string 对象的长度是可以改变的
C.length()和size() 返回值相同
D.string不必须以'\0'结尾,且'\0'不计入 length()
第10题
考虑以下C++函数:
void solve(int &a, int b) {
a = a + b;
b = a - b;
a = a - b;
}
int main() {
int x = 5, y = 10;
solve(x, y);
}
在main函数调用solve后,x 和 y 的值分别是?
A.5,10
B.10,5
C.10,10
D.5,5
【答案】:C
【解析】
初始:x = 5, y = 10
a = a + b = 5 + 10 = 15 (x变为15)
b = a - b = 15 - 10 = 5(局部变量b变为5,y不变)
a = a - b = 15 - 5 = 10(x变为10)
第11题
一个8×8的棋盘,左上角坐标为(1, 1),右下角为(8, 8)。一个机器人从(1, 1)出发,每次只能向右或向下走一格。要到达(4, 5),有多少种不同的路径?
A.20
B.35
C.56
D.70
【答案】:B
【解析】
使用递推法,f[i][j] = f[i-1][j] + f[i][j-1],f[1][j] = 1,f[i][1] =1,计算得到f[4][5] = 35
第12题
某同学用冒泡排序对数组{6,1,5,2,4}进行升序排序,请问需要进行多少次元素交换?
A.5
B.6
C.7
D.8
【答案】:B
【解析】
数组{6,1,5,2,4}:
第1轮:4次交换得到{1,5,2,4,6}
第2轮:2次交换得到{1,2,4,5,6}
总计:6次交换
第13题
十进制数 \(720_{10}\) 和八进制数 \(270_8\) 的和用十六进制表示是多少?
A.\(388_{16}\)
B.\(3DE_{16}\)
C.\(288_{16}\)
D.\(720_{10}\)
【答案】:A
【解析】
\(270_8\) = \(184_{10}\)
720 + 184 = 904 = \(388_{16}\)
第14题
一棵包含 1000 个结点的完全二叉树,其叶子结点的数量是多少?
A.499
B.512
C.500
D.501
【答案】:C
【解析】
1000个节点的完全二叉树,最后一层叶子节点数为 1000 - 2^9-1 = 489,对应上一层节点数245,即 256-245 = 11个没有子节点。所以叶子节点为489 + 11 = 500
第15题
给定一个初始为空的整数栈 S 和一个空的队列P。我们按顺序处理输入的整数队列A:7,5,8,3,1,4,2。对于队列A中的每一个数,执行以下规则:如果该数是奇数,则将其压入栈 S;如果该数是偶数,且栈 S 非空,则弹出一个栈顶元素,并加入到队列 P 的末尾;如果该数是偶数,且栈 S 为空,则不进行任何操作。当队列 A 中的所有数都处理完毕后,队列 P 的内容是什么?( )
A.5,1,3
B.7,5,3
C.3,1,5
D.5,1,3,7
【答案】:A
【解析】
模拟过程
| 当前数 | 操作 | 栈S | 队列P |
|---|---|---|---|
| 7 | 压入S | [7] | [] |
| 5 | 压入S | [7,5] | [] |
| 8 | 弹出栈顶->加入P | [7] | [5] |
| 3 | 压入S | [7,3] | [5] |
| 1 | 压入S | [7,3,1] | [5] |
| 4 | 弹出栈顶->加入P | [7,3] | [5,1] |
| 2 | 弹出栈顶->加入P | [7] | [5,1,3] |
阅读程序
#include <algorithm>
#include <cstdio>
#include <cstring>
inline int gcd(int a, int b) {
if (b == 0)
return a;
return gcd(b, a % b);
}
int main() {
int n;
scanf("%d", &n);
int ans = 0;
for (int i=1; i<=n; ++i) {
for (int j=i+1; j<=n; ++j) {
for (int k=j+1; k<=n; ++k) {
if (gcd(i, j) == 1 && gcd(j, k) == 1
&& gcd(i, k) == 1) {
++ans;
}
}
}
}
printf("%d\n", ans);
return 0;
}
第16题
当输入为2时,程序并不会执行第16行的判断语句。( )
A.正确
B.错误
【答案】:A
【解析】
输入n=2时,最内层循环不会执行,也不会执行第16行
第17题
将第16行中的"&& gcd(i,k)==1"删去不会影响程序运行结果。( )
A.正确
B.错误
【答案】:B
【解析】
题目要求是三元组(i,j,k)之间两两互质,修改为(i,j)之间判断,肯定不行
第18题
当输入的n≥3的时候,程序总是输出一个正整数。( )
A.正确
B.错误
【答案】:A
【解析】
对于n≥3,至少存在一个合法三元组(1,2,3)满足两两互质。
第19题
将第7行的"gcd(b, a%b)"改为"gcd(a, a%b)"后,程序可能出现的问题是( )。
A.输出的答案大于原答案。
B.输出的答案小于原答案。
C.程序有可能陷入死循环。
D.可能发生整型溢出问题。
【答案】:B
【解析】
举例说明:原版本gcd(6,4) = 2,修改后gcd(6, 4) = 6,即总是返回第一个参数,所以条件变为 i == 1 && j == 1 && i == 1,不满足题目中的if条件,最后ans始终为0。而原题目ans必然是正整数,所以选B。
第20题
当输入为8的时候,输出为( )。
A.37
B.42
C.35
D.25
【答案】:D
【解析】
当n=8时,枚举所有可能的三元组并检查是否两两互质:
i=1的情况:
(1,2,3),(1,2,5),(1,2,7):3个
(1,3,4),(1,3,5),(1,3,7),(1,3,8):4个
(1,4,5),(1,4,7):2个
(1,5,6),(1,5,7),(1,5,8):3个
(1,6,7):1个
(1,7,8):1个
小计:14个
i=2的情况:(2,3,5),(2,3,7),(2,5,7):3个
i=3的情况:(3,4,5),(3,4,7),(3,5,7),(3,5,8),(3,7,8):5个
i=4的情况:(4,5,7):1个
i=5的情况:(5,6,7),(5,7,8):2个
总计:14+3+5+1+2 = 25
第21题
调用gcd(36, 42)会返回( )。
A.6
B.252
C.3
D.2
【答案】:A
【解析】
36和42的最小公约数是6
#include <algorithm>
#include <cstdio>
#include <cstring>
#define ll long long
int n, k;
int a[200007];
int ans[200007];
int main() {
scanf("%d%d", &n, &k);
for (int i=1; i<=n; ++i) {
scanf("%d", &a[i]);
}
std::sort(a+1, a+n+1);
n = std::unique(a+1, a+n+1) - a - 1;
for (int i=1, j=0; i<=n; ++i) {
for (; j<i && a[i]-a[j+1]>k; ++j)
;
ans[i] = ans[j] + 1;
}
printf("%d\n", ans[n]);
return 0;
}
第22题
当输入为"3 1 3 2 2 1"时,输出结果为2。( )
A.正确
B.错误
【答案】:A
【解析】
排序、去重后为[1,2,3]。
i=1:ans[1] = 1(第16行for循环不执行)
i=2:ans[2] = ans[0] + 1 = 1
i=3:ans[3] = ans[1] + 1 = 2
第23题
假设输入的n为正整数,输出的答案一定小于等于n,大于等于1。( )
A.正确
B.错误
【答案】:A
【解析】
ans[n]中的n是去重后的元素个数,且ans[0]=0,ans[i]>=1,所以ans[n]满足 1<=ans[n]<=n。
第24题
将第14行的"n=std::unique(a+1, a+n+1)-a-1;"删去后,有可能出现与原本代码不同的输出结果。( )
A.正确
B.错误
【答案】:B
【解析】
本题程序功能是"划分成首尾差不超过k"的连续子序列,所以就算有重复元素,也会在连续子序列的中间部分,不会影响到首尾之差的判断
第25题
假设输入的 a 数组和 k 均为正整数,执行第18行代码时,一定满足的条件不包括( )。
A.j<=i
B.a[i]-a[j]>k
C.j<=n
D.a[j]<a[i]
【答案】:B
【解析】
内层循环的条件是j < i,退出时 j 可能等于 i,因此j <= i 总是成立,A正确
内层循环退出时,a[i] - a[j+1] <= k,但 a[i] - a[j] 的值未被约束,a[i] - a[j] > k 并非总是成立的
j 的初始值为0,最大值为 i,而i <= n。因此 j <= n 总是成立,C正确
数组a是排序且去重后的,且 j < i,因此a[j] < a[i],D成立
第26题
当输入的n=100,k=2,a={1, 2, ..., 100} 时,输出为( )。
A.34
B.100
C.50
D.33
【答案】:A
【解析】
输入为严格递增数组[1,2,,...,100],差值为k=2。
i=1:第一个元素,ans[1]=1。
对后续每个元素a[i],更新条件是a[i] - a[j] > k。每两轮后形成新的分组。
每 k+1=3 个数为一个分组,最终分组数为:\(\lceil 100/3\rceil=34\)。输出结果为34。
第27题
假设输入的 a 数组和 k 均为正整数,但 a 数组不一定有序,则若误删去第13行的"std::sort(a+1,a+n+1); ",程序有可能出现的问题有( )。
A.输出的答案比原本答案更大
B.输出的答案比原本答案更小
C.出现死循环行为
D.以上均可能发生
【答案】:B
【解析】
尝试枚举反例,如a = [4,1,2,3],正常输出2,但删除第13行后输出1,直接选B
#include <algorithm>
#include <cstdio>
#include <cstring>
#define ll long long
int f[5007][5007];
int a[5007], b[5007];
int n;
int main() {
scanf("%d", &n);
for (int i=1; i<=n; ++i) {
scanf("%d", &a[i]);
}
for (int i=1; i<=n; ++i) {
scanf("%d", &b[i]);
}
for (int i=1; i<=n; ++i) {
for (int j=1; j<=n; ++j) {
f[i][j] = std::ax(f[i][j], std::max(f[i-1][j], f[i][j-1]));
if (a[i] == b[j]) {
f[i][j] = std::max(f[i][j], f[i-1][j-1] + 1);
}
}
}
printf("%d\n", f[n][n]);
return 0;
}
第28题
当输入"4 1 2 3 4 1 3 2 2"时,输出为2。( )
A.正确
B.错误
【答案】:A
【解析】
a序列[1, 2, 3, 4],b序列[1, 3, 2, 2],由公共子序列的定义,两个序列的LCS为[1, 2],其长度即为2
第29题
当程序运行完毕后,对于所有的 1≤i, j≤n,都一定有 f[i][j]≤f[n][n]。( )
A.正确
B.错误
【答案】:A
【解析】
f[n][n]作为最终答案,a、b两个序列显然包含了其所有的前缀,因此f[n][n]一定不会比 f[i][j]更差。
第30题
30.将第18行的"f[i][j]=std::max(f[i][j], std::max(f[i-1][j], f[i][j-1])); "删去后,并不影响程序运行结果。( )
A.正确
B.错误
【答案】:B
【解析】
如果没有从f[i-1][j]或f[i][j-1]到f[i][j]的转移,就无法表示 a[i] 或b[j]不选入公共子序列的情形。
第31题
输出的答案满足的性质有( )。
A.小于等于n
B.大于等于0
C.不一定大于等于1
D.以上均是
【答案】:D
【解析】
序列长度一定是非负数(大于等于0),且小于等于序列的最长长度。通过A、B两项即可判断选D
第32题
如果在16行的循环前加上以下两行:"std::sort(a+1, a+n+1);std::sort(b+1, b+n+1)",则答案会( )。
A.变大或不变
B.变小或不变
C.一定变大
D.不变
【答案】:A
【解析】
按照第28题的举例,答案变大了,所以排除B、D。假设a和b没有公共序列,那怎么排序也都是0,所以选A
第33题
如果输入的a={1, 2, ..., n},而且b 数组中数字均为1~n中的正整数,则上述代码等价于下面哪个问题:( )。
A.求b数组去重后的长度
B.求b数组的最长上升子序列
C.求b数组的长度
D.求b数组的最大值
【答案】:B
【解析】序列a为1,2,...,n时,其与序列b的LCS中,所有元素也一定单调递增,故其为序列b的一个上升子序列。
完善程序
(字符串解码)"行程长度编码"(Run-Length Encoding)是一种无损压缩算法,常用于压缩重复字符较多的数据,以减少存储空间。假设原始字符串不包含数字字符。压缩规则如下:i) 如果原始字符串中一个字符连续出现N次(N≥2),在压缩字符串中它被表示为"字符+数字 N"。例如,编码"A12"代表12个连续的字符A。ii) 如果原始字符串中一个字符只出现1次,在压缩字符串中它就表示为该字符本身。例如,编码"B"代表1个字符B。
以下程序实现读取压缩字符串并输出其原始的、解压后的形式。试补全程序。
#include <cctype>
#include <iostream>
#include <string>
using namespace std;
int main() {
string z;
cin >> z;
string s = "";
for (int i=0; i<z.length((); ) {
char ch = z[i];
if (__1__ && isdigit(z[i+1])) {
i++;
int count = 0;
while (i < z.length() && isdigit(z[i])) {
count = __2__
i++;
}
for (int j=0; j<__3__; ++j) {
s += ch;
}
} else {
s += __4__;
__5__;
}
}
cout << s << endl;
return 0;
}
第33题
1处应填( )
A.i < z.length()
B.i - 1 >= 0
C.i + 1 < z.length()
D.isdigit(z[i])
【答案】:C
【解析】
第14行判断z[i+1]是否为数字字母,这同时要求z[i+1]存在,故应判断 i+1 是否在下标范围内。
第34题
2处应填( )
A.count + (z[i] - '0')
B.count * 10 + (z[i] - '0')
C.z[i] - '0'
D.count + 1
【答案】:B
【解析】
此处应时将字符串转为数值,应该使用秦九韶算法拼接字符变成数字
第35题
3处应填( )
A.count - 1
B.count
C.10
D.z[i] - '0'
【答案】:B
【解析】
上面得到了字符 ch 应连续出现的次数count,此处应连续向s中拼接count次字符ch
第36题
4处应填( )
A.z[i+1]
B.ch
C.z.back()
D.(char)z[i] + 1
【答案】:B
【解析】
此处处理字符只出现一次的情形。
第37题
5处应填( )
A.i--
B.i = i + 2
C.i++
D.//不执行任何操作
【答案】:C
【解析】
每次处理z[i]后,应将 i 右移一位,后续处理下一个字符。
(精明与糊涂)有N个人,分为两类:i) 精明人:永远能正确判断其他人是精明还是糊涂;ii) 糊涂人:判断不可靠,会给出随机的判断。已知精明人严格占多数,即如果精明人有k个,则满足k>N/2。
你只能通过函数query(i, j)让第i个人判断第j个人,返回 true 表示判断结果为"精明人";返回 false 表示判断结果为"糊涂人"。你的目标是:通过这些互相判断,找出至少一个百分之百能确定的精明人。同时,你无需关心 query(i, j)的内部实现。
以下程序利用"精明人占多数"的优势,设想一个"消除"的过程,让人们互相判断并进行抵消。经过若干轮抵消后,最终留下的候选者必然属于多数派,即精明人。
例如,假设有三个人0、1、2,如果0说1是糊涂人,而1也说0是糊涂人,则0和1至少有一个是糊涂人。程序将同时淘汰0和1,由于三人里至少有两个精明人,我们确定2是精明人。
试补全程序。
#include <iostream>
#include <vector>
using namespace std;
int N;
bool query(int i, int j);
int main() {
cin >> N;
int candidate = 0;
int count = __1__;
for (int i=1; i<N; ++i) {
if (__2__) {
candidate = i;
count = 1;
} else {
if (__3__) {
__4__;
} else {
count++;
}
}
}
cout << __5__ << endl;
return 0;
}
第38题
1处应填( )
A.0
B.1
C.N
D.-1
【答案】:B
【解析】
count 表示与候选人 candidate 为同类人的数量,任何人和他自己显然是同类人,故初始时和更换后,都应设置为1人。
第39题
2处应填( )
A.count < 0
B.count == 1
C.count == 0
D.query(candidate, i) == false
【答案】:C
【解析】
count = 0 时,不同类人对旧候选人的投标相互抵消,此时,可以另立新的候选人。
第40题
3处应填( )
A.query(candidate, i) == false
B.query(i, candidate) == true
C.query(candidate, i) == false && query(i, candidate) == false
D.query(candidate, i) == false || query(i, candidate) == false
【答案】:D
【解析】
3处相反条件是 i 和 candidate 为“同类人”,那么3处应判断 i 和 candidate 不是同类人。
第41题
4处应填( )
A.count--
B.break
C.count++
D.candidate = i
【答案】:A
【解析】
题面已经提示了,通过消除过程让人们互相判断并抵消,所以第22行是count++,这里应该就是count--
第42题
5处应填( )
A.N-1
B.count
C.candidate
D.0
【答案】:C
【解析】
candidate即表示经过若干轮抵消后留下的候选人。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号