如何快速求解【知道二叉树的先序遍历/后序遍历&中序遍历，求其后序遍历/先序遍历】的问题

如何快速求解【知道二叉树的先序遍历/后序遍历&中序遍历，求其后序遍历/先序遍历】的问题

前言

在做CSP-J初赛真题的时候，在2019年的题中(T14)，被卡住了。

尝试使用递归的解法进行解题，彻底累死了，最后只能蒙上一个答案

得到了一个鲜红的 \(\color{Red}\texttt{WA}\)。

赛后补题的时候查找资料发现了一个非常好的方法（链接在文末）

步骤

1.如果是先序遍历，竖着写下来，后序则反着写下来

2.在底下写中序遍历

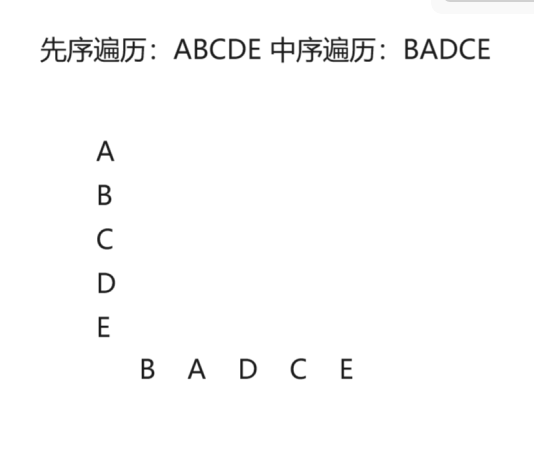
3.画表格

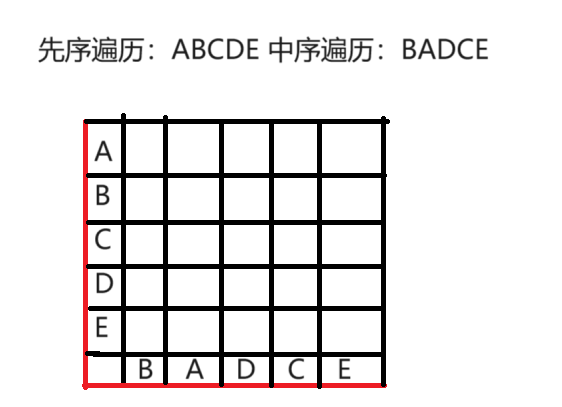
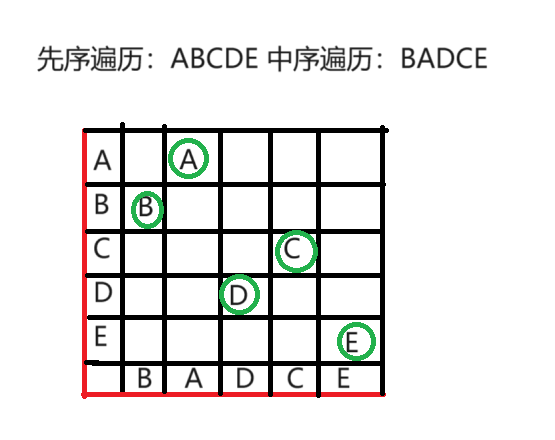
4.将纵轴上的点和横轴上的一一匹配起来

5.连线并提取得到答案，注意左子树所有节点在父节点的左方（这句话在后面有解释）

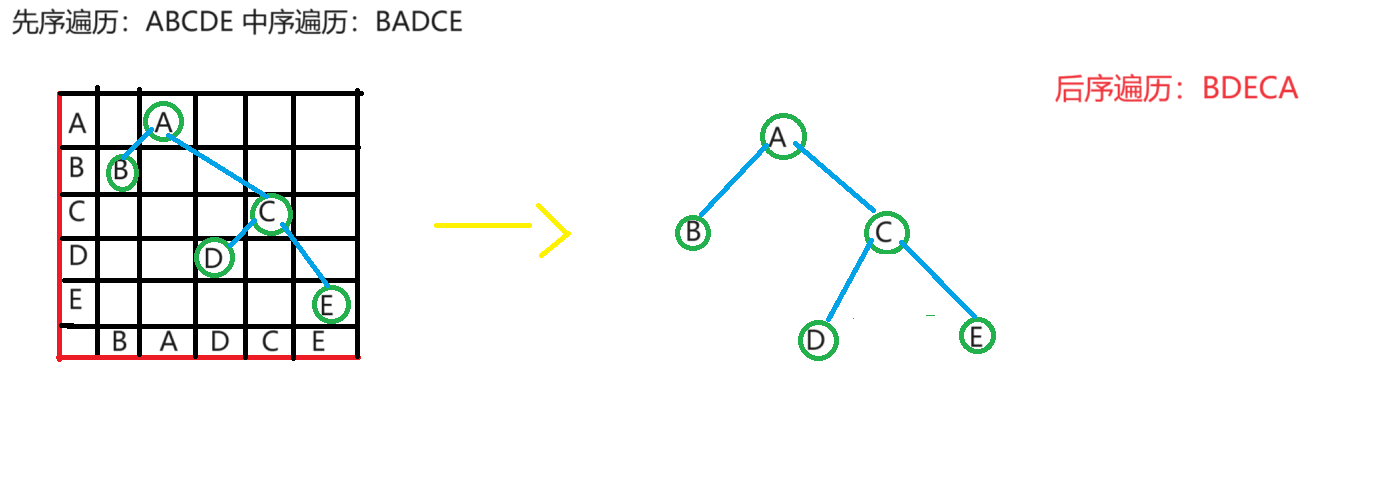
解释

那为什么能这样？

要从它的思想说起。

它的思想实际上还是根据先/后序遍历对于中序遍历进行分解

因为先序遍历是：根左右 的顺序，所以每次都能获取到根

而后序遍历反过来也有同样的效果。

并且中序遍历的顺序是：左根右 的顺序，根据根，可以将中序遍历确定左子树和右子树。

所以每一次匹配都是相当于对中序遍历进行了一次剖解，这就限定了 \(\color{Red}\texttt{第五步}\) 的那句话。

明白了吗？不明白可以去看一下底下的视频

---

文末

注：本文灵感来源于此视频,但是本文章具有更加详细的解释和证明